ТЕМА. ПРЕОБРАЗОВАНИЕ КООРДИНАТ. КО- КОНТРАВАРИАНТНЫЕ ВЕЛИЧИНЫ
п.1. Преобразование координат характеризуется соотношением 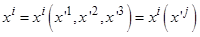 и выражает отображение областей изменения переменных
и выражает отображение областей изменения переменных  и
и  друг на друга. Штрих в дальнейшем означает переменную в новой системе координат. Отображение является непрерывным, взаимно однознач-ным, если якобиан преобразования
друг на друга. Штрих в дальнейшем означает переменную в новой системе координат. Отображение является непрерывным, взаимно однознач-ным, если якобиан преобразования  ; при этом якобиан обратного преобразования
; при этом якобиан обратного преобразования  .
.
Задача 1. Записать явный вид соотношения 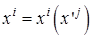 , если
, если 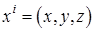 – декартовы координаты, а
– декартовы координаты, а 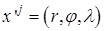 – сферические (рис.1), и якобиана
– сферические (рис.1), и якобиана 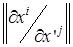 .
.
Ответ.
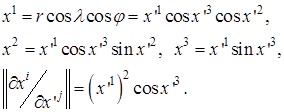
Задача 2. Записать явный вид преобразования, обратного указанному выше.
Ответ: 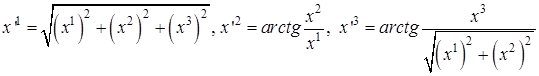 .
.
Поменяв местами штрих, придем к записи 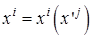 . Особые точки преобразования
. Особые точки преобразования 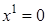 .
.
п.2. Преобразование 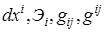 .
.
Задача 3. Записать формулу преобразования дифференциала координат при преобразовании 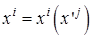 .
.
Решение. При условии, что 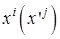 – дифференцируемая по всем переменным функция, можно записать:
– дифференцируемая по всем переменным функция, можно записать: 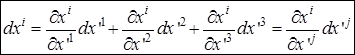 .
.
Результат можно представить в матричной форме: 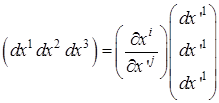 .
.
Задача 4. Вывести формулу преобразования базисных векторов 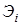 .
.
Решение. Исходим из определения  . По формуле дифференцирования сложных функций имеем:
. По формуле дифференцирования сложных функций имеем:  . Получаем искомую формулу преобразования:
. Получаем искомую формулу преобразования:
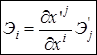 .
.
Преобразование базисных векторов 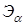 и дифференциалов
и дифференциалов  осуществляется с помощью матриц
осуществляется с помощью матриц 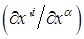 и
и  , обратных друг к другу. Поэтому величины с индексами сверху называются контравариантным и по этим индексам (т.е. преобразующихся "противоположно" преобразованию базиса), а величины с индексами внизу называются ковариантными. Полезным для запоминания является мнемоническое правило; ковариантный индекс «производная от новой переменной / по старой.
, обратных друг к другу. Поэтому величины с индексами сверху называются контравариантным и по этим индексам (т.е. преобразующихся "противоположно" преобразованию базиса), а величины с индексами внизу называются ковариантными. Полезным для запоминания является мнемоническое правило; ковариантный индекс «производная от новой переменной / по старой.
Задача 5. Какова формула преобразования элементов метрической матрицы  при переходе к новым переменным.
при переходе к новым переменным.
Решение. Используем определение 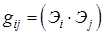 .
.
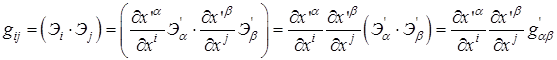 .
.
Здесь  – значение элемента матрицы преобразования в точке, где выполняется преобразование.
– значение элемента матрицы преобразования в точке, где выполняется преобразование.
Задача 6. Вывести формулу преобразования 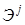 .
.
Решение. Согласно определению  . Выполняем преобразования, используя полученные ранее выражения:
. Выполняем преобразования, используя полученные ранее выражения: 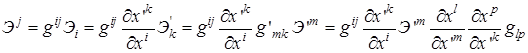 . По правилу "частного" имеем:
. По правилу "частного" имеем: 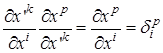 . Тогда получаем выражения:
. Тогда получаем выражения:
 .
.
Получена формула
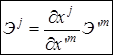 .
.
Задача 7. Показать, что ортогональные проекции вектора на оси косоугольной системы координат преобразуются как ковариантные переменные.
Решение. Ортогональную проекцию вектора  на направление вектора
на направление вектора 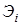 будем обозначать
будем обозначать  . По определению
. По определению 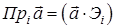 . Базисный вектор
. Базисный вектор 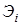 в косоугольной, но прямолинейной системе координат, орт. Имеем:
в косоугольной, но прямолинейной системе координат, орт. Имеем:
 ,
,
т.е. 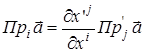 , так преобразуются ковариантные переменные.
, так преобразуются ковариантные переменные.
Дополнительные задачи
1. Доказать, что если  – декартовые координаты, а
– декартовые координаты, а  – произвольные криволинейные, связанные соотношением
– произвольные криволинейные, связанные соотношением 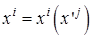 , то компоненты метрической матрицы
, то компоненты метрической матрицы  удовлетворяют равенству
удовлетворяют равенству 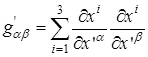 .
.
2. Используя связь декартовых и сферических координат, получить элементы метрической матрицы в сферических координатах, на основании задания 1. Сравнить с предыдущими результатами.
3. Задана прямолинейная, косоугольная система координат, угол между двумя координатными линиями в точке равен  , третья координатная линия перпендикулярна первым двум. Определить величины и направления базисных векторов
, третья координатная линия перпендикулярна первым двум. Определить величины и направления базисных векторов 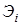 и
и  .
.
4. Записать формулы преобразования сферической системы координат в цилиндрическую и найти якобиан преобразования.
5. Показать, что частные производные произвольной функции 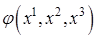 преобразуются при переходе к новой системе координат как ковариантные величины.
преобразуются при переходе к новой системе координат как ковариантные величины.
6. Вывести формулу преобразования  при переходе от
при переходе от  к
к  .
.

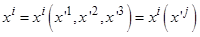 и выражает отображение областей изменения переменных
и выражает отображение областей изменения переменных  и
и  друг на друга. Штрих в дальнейшем означает переменную в новой системе координат. Отображение является непрерывным, взаимно однознач-ным, если якобиан преобразования
друг на друга. Штрих в дальнейшем означает переменную в новой системе координат. Отображение является непрерывным, взаимно однознач-ным, если якобиан преобразования  ; при этом якобиан обратного преобразования
; при этом якобиан обратного преобразования  .
.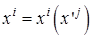 , если
, если 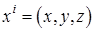 – декартовы координаты, а
– декартовы координаты, а 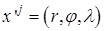 – сферические (рис.1), и якобиана
– сферические (рис.1), и якобиана 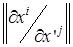 .
.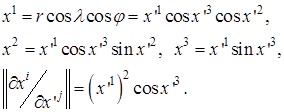
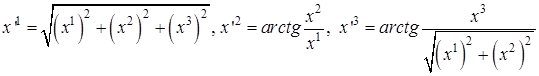 .
.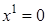 .
.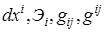 .
.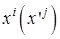 – дифференцируемая по всем переменным функция, можно записать:
– дифференцируемая по всем переменным функция, можно записать: 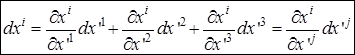 .
.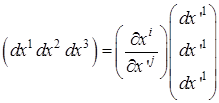 .
.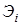 .
. . По формуле дифференцирования сложных функций имеем:
. По формуле дифференцирования сложных функций имеем:  . Получаем искомую формулу преобразования:
. Получаем искомую формулу преобразования: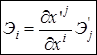 .
.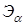 и дифференциалов
и дифференциалов  осуществляется с помощью матриц
осуществляется с помощью матриц 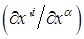 и
и  , обратных друг к другу. Поэтому величины с индексами сверху называются контравариантным и по этим индексам (т.е. преобразующихся "противоположно" преобразованию базиса), а величины с индексами внизу называются ковариантными. Полезным для запоминания является мнемоническое правило; ковариантный индекс «производная от новой переменной / по старой.
, обратных друг к другу. Поэтому величины с индексами сверху называются контравариантным и по этим индексам (т.е. преобразующихся "противоположно" преобразованию базиса), а величины с индексами внизу называются ковариантными. Полезным для запоминания является мнемоническое правило; ковариантный индекс «производная от новой переменной / по старой. при переходе к новым переменным.
при переходе к новым переменным.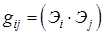 .
.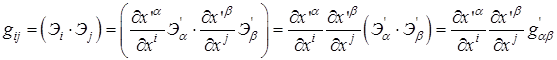 .
. – значение элемента матрицы преобразования в точке, где выполняется преобразование.
– значение элемента матрицы преобразования в точке, где выполняется преобразование.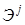 .
. . Выполняем преобразования, используя полученные ранее выражения:
. Выполняем преобразования, используя полученные ранее выражения: 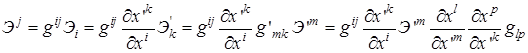 . По правилу "частного" имеем:
. По правилу "частного" имеем: 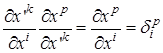 . Тогда получаем выражения:
. Тогда получаем выражения: .
.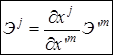 .
. на направление вектора
на направление вектора  . По определению
. По определению 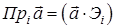 . Базисный вектор
. Базисный вектор  ,
,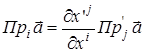 , так преобразуются ковариантные переменные.
, так преобразуются ковариантные переменные. удовлетворяют равенству
удовлетворяют равенству 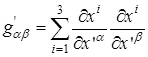 .
. , третья координатная линия перпендикулярна первым двум. Определить величины и направления базисных векторов
, третья координатная линия перпендикулярна первым двум. Определить величины и направления базисных векторов  .
. преобразуются при переходе к новой системе координат как ковариантные величины.
преобразуются при переходе к новой системе координат как ковариантные величины. при переходе от
при переходе от 


