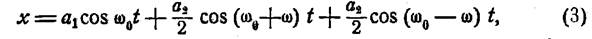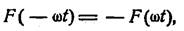Представление негармонических колебательных процессов при помощи гармонических колебаний.Представление негармонических колебательных процессов при помощи гармонических колебаний.
До сих пор мы рассматривали в основном простое гармоническое колебательное движение, т. е. движение, при котором смещение х колеблющейся частицы из положения равновесия имеет вид:
или, что то же самое
где а — амплитуда колебаний, ω — круговая частота колебаний, α и α' — начальные фазы. Такое колебание графически изображается синусоидой. Однако реальные колебания могут лишь более или менее точно походить на строго синусоидальные колебания, хотя бы потому, что всякие реальные колебания сопровождаются затуханием. Кроме того, весьма часто колебания, вообще, носят более сложный характер. Тем не менее рассмотрение гармонических колебаний имеет большое значение, так как сложное колебание можно представить как сумму гармонических колебаний. При сложении двух гармонических колебательных движений x1 и х2 совершающихся вдоль одной а той же прямой и имеющих одинаковую частоту ω, результирующее колебание является также гармоническим колебательным движением. Но так обстоит дело лишь при сложении колебаний одной частоты. При сложении двух гармонических колебательных движений разных частот суммарное колебание носит более сложный характер.
На рис. в верхней строке графически изображено гармоническое колебательное движение определенной частоты ω1 и определенной амплитуды а1 (по оси ординат отложено смещение x по оси абсцисс — время). В средней строке изображено другое гармоническое колебание х2, происходящее с частотой ω2, в 4,5 раза меньшей, чем частота ω1 первого движения, и с амплитудой а2 = 2,5 а1. Наконец, в нижней строке представлено колебание, являющееся суммой двух первых; смещение х точки, совершающей это сложное колебание, в каждый данный момент равно х = х1 + х2
Мы могли бы поставить задачу обратно и, имея сложное колебание заданным, посмотреть, на сумму каких гармонических колебательных движений оно разложимо. В случае сложного колебания, изображенного на нижней строке рис., оно разложимо на два гармонических колебания, изображенных на двух других строках рис.
Аналогично можно себе представить иное сложное колебание, амплитуда которого медленно (по сравнению с периодом самих колебаний) меняется по какому-либо другому закону. Такого рода колебание носит название модулированного колебания. Модулированное колебание не представляет собою гармонического колебательного движения, но может быть разложено на ряд гармонических колебательных движений. Возьмем для примера колебание
амплитуда которого меняется по закону:
где a1 и а2 постоянны, причем считаем а2< а1 и ω<< ω0. Этот, закон означает, что амплитуда а меняется со временем между значениями ω1 - ω2 и ω2 – ω1. Подставив приведенное значение для а в выражение для х, получим
или
т. е. рассматриваемое модулированное колебание может быть разложено на сумму трех гармонических колебательных движений с частотами ω0, ω0 + ω и ω0 - ω и соответственно с амплитудами а1, а2/2 и а2/2.
Результат сложения двух гармонических колебаний зависит от их частот, амплитуд и начальных фаз. В зависимости от значения частот, фаз и амплитуд могут быть получены весьма разнообразные суммарные колебания. Еще более сложный характер колебаний получится при сложении трех и более гармонических колебательных движений. Обратно, колебание весьма сложного характера может быть разложено на достаточное число гармонических колебаний различных амплитуд и частот.
В теории тригонометрических рядов показывается, что периодическую функцию с периодом 2π
можно представить в виде бесконечного тригонометрического ряда
носящего название ряда Фурье; коэффициенты А0, A1, A1, А3... и B1, B2, В3... для данного вида F(ωt) вычисляются по определенным формулам. Для четной функции, т. е. такой, которая сохраняет свое значение при изменении знака аргумента на обратный:
все коэффициенты B1, B2, В3... равны нулю, так что разложение в ряд принимает вид:
Для нечетной функции, т. е. для такой функции, которая меняет знак при изменении знака аргумента:
все коэффициенты А0, A1, A1, А3,... равны нулю, так что разложение в ряд принимает вид:
Таким образом, видно, что, вообще говоря, любое периодическое колебание может быть математически представлено как сумма гармонических колебаний кратных частот ω, 2ω, Зω и т.д.
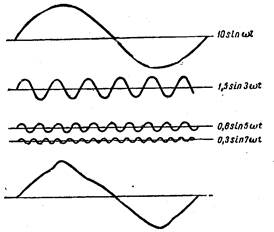
На рис. внизу представлено колебание, имеющее вид почти ломаной линии;
выше представлены четыре синусоиды, на которые оно разлагается. Аналитически это разложение имеет вид:
в этом разложении В1= 10а, B3 = -1,5а, B5 = 0,6a, B7 = -0,3а, все остальные коэффициенты Bi равны нулю.
Результат разложения сложного колебания в ряд Фурье можно представить, записав все те частоты, амплитуды которых отличны от нуля, и значения соответствующих им амплитуд. Такую запись весьма удобно делать графически, отложив по оси абсцисс шкалу частот и проводя в соответственных местах оси абсцисс вертикальные линии, длина которых в определенном масштабе изображает амплитуду. Такой график носит название спектра данного колебания. На рис. представлен спектр сложного колебания, изображенного на нижней строке вышерассмотренного рис.
Согласно разложению (7), этот спектр содержит четыре линии с частотами ω, Зω, 5ω и 7 ω; длины этих линий в некотором определенном масштабе равны 10; 1,5; 0,6 и 0,3 единицам длины. Изображение сложных колебаний с помощью такого рода спектров не полно в том смысле, что оно дает лишь частоты и амплитуды составляющих гармонических колебаний, не давая их начальные фазы; однако для многих случаев знания частот и амплитуд вполне достаточно. До сих пор мы рассматривали разложение на сумму гармонических колебаний сложных колебаний, имеющих периодический характер. Движение может, однако, будучи колебательным, вместе с тем не носить периодического характера. В качестве примера можно привести затухающее колебание, изображенное на рис.
Здесь амплитуда колебаний непрерывно затухает, так что некоторое определенное состояние движения осуществляется один раз. Такое непериодическое движение нельзя разложить в ряд Фурье с прерывным рядом частот ω, 2ω, Зω и т.д. Оно может быть разложено на бесконечное множество гармонических колебательных движений, причем частоты „соседних" колебаний будут бесконечно мало отличаться друг от друга, а амплитуды ΔАi отдельных элементарных колебаний будут бесконечно малы. Графически такому колебанию уже не соответствует спектр, состоящий из отдельных линий („линейчатый спектр'): ему соответствует непрерывный спектр, что означает присутствие колебаний со „всеми" частотами. Для графического изображения непрерывного спектра отложим по оси абсцисс снова частоты ω, а по оси ординат - отношение ΔАi/Δ ωi. Тогда кривая на таком графике даст „распределение амплитуд" по частотам в сплошном спектре данного сложного колебания. На рис. еще раз представлено затухающее колебание и „распределение амплитуд" по частотам в сплошном спектре этого колебания. Ординаты графика, умноженные на соответственный интервал частот дают среднюю амплитуду колебаний в этом интервале частот.
Как видно из рис., кривая имеет максимум, который оказывается тем острее, чем слабее затухание. Для иных непериодических движений получится сплошной спектр с иным распределением амплитуд по частотам.
|