Несобственные интегралы с бесконечными пределами интегрирования (первого рода)Определение 9. Пусть функция
Если этот предел существует и конечен, то интеграл называется сходящимся. Если же указанный предел не существует или бесконечен, то Аналогично определяется несобственный интеграл на промежутке
Несобственный интеграл с двумя бесконечными пределами определяется так:
где Данный интеграл сходится, если сходятся оба интеграла в правой части. Если хотя бы один из интегралов в правой части равенства расходится, то и Если непрерывная функция
Пример 48. Вычислить несобственный интеграл или доказать его расходимость Решение. Имеем
см. рисунок 6
Следовательно, интеграл сходится и его значение равно Пример 49. Вычислить несобственный интеграл или доказать его расходимость Решение.
то есть Пример 50. Вычислить несобственный интеграл или доказать его расходимость Решение.
Но Пример 51. Вычислить несобственный интеграл или доказать его расходимость Решение. Пусть
Таким образом, Пусть
то есть при Пусть
то есть при Итак, имеем Этот интеграл часто используется в признаке сравнения в качестве эталонного. Пример 52. Вычислить несобственный интеграл или доказать его расходимость Решение.
Итак, Не всегда удается выяснить сходимость несобственных интегралов с помощью определения, поэтому используют признаки сравнения. Теорема 10. Если функции Теорема 11. Если функции Пример 53. Исследовать на сходимость несобственный интеграл Решение. Рассмотрим функции Данные функции непрерывны на промежутке Пример 54. Исследовать на сходимость несобственный интеграл Решение. Рассмотрим функции
Так как Если функция Теорема 12. Если интеграл Последний интеграл называется абсолютно сходящимся.
|

 определена и непрерывна на промежутке
определена и непрерывна на промежутке 
 . Тогда существует определенный интеграл
. Тогда существует определенный интеграл  . При изменении
. При изменении  интеграл изменяется, он является непрерывной функцией
интеграл изменяется, он является непрерывной функцией  называется несобственным интегралом первого рода от функции
называется несобственным интегралом первого рода от функции  .
. называется расходящимся.
называется расходящимся.
 .
. ,
,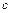 – произвольное число.
– произвольное число. расходится.
расходится. на промежутке
на промежутке  ,
,  и осью абсцисс (рисунок 5).
и осью абсцисс (рисунок 5).
 .
.

 при
при 


 .
.

 .
. .
.


 .
.
 при
при  не существует и
не существует и  .
. , тогда
, тогда .
. – расходится.
– расходится. , тогда
, тогда
 так как
так как  , а
, а  ,
, сходится и равен
сходится и равен  .
.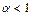 , тогда
, тогда так как
так как  , а
, а  , тогда при
, тогда при  ,
, расходится.
расходится.
 .
.
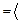 при
при  , при
, при  (см. рисунок 6)
(см. рисунок 6)  .
. .
.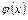 непрерывны на промежутке
непрерывны на промежутке  и удовлетворяют условию
и удовлетворяют условию  , то из сходимости интеграла
, то из сходимости интеграла 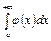 следует сходимость интеграла
следует сходимость интеграла  , а из расходимости интеграла
, а из расходимости интеграла 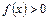 ,
,  ) на промежутке
) на промежутке  , причем
, причем 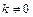 , то интегралы
, то интегралы  и
и  одновременно сходятся или расходятся.
одновременно сходятся или расходятся. .
. и
и 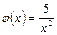 .
. и удовлетворяют условию
и удовлетворяют условию  , то есть
, то есть  , так как
, так как  . Интеграл
. Интеграл  (см. пример 51) сходится и равен
(см. пример 51) сходится и равен 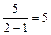 , следовательно, по теореме 10 сходится и интеграл
, следовательно, по теореме 10 сходится и интеграл  и его значение меньше 5.
и его значение меньше 5. .
. и
и  . Данные функции непрерывны и положительны на промежутке
. Данные функции непрерывны и положительны на промежутке  разделим и числитель и знаменатель на
разделим и числитель и знаменатель на 
 при
при  .
. и
и  сходится, то сходится и исходный интеграл
сходится, то сходится и исходный интеграл  , то имеет место следующая теорема.
, то имеет место следующая теорема. сходится, то сходится и интеграл
сходится, то сходится и интеграл 


