Устойчивость работы насоса в сети. Осевые насосы

 

Анализ устойчивости функционирования системы насос-контур циркуляции выполнен для простейшей схемы рис. 13.1.

 

В замкнутом контуре циркуляции, состоящем из нескольких участков различной длины Li и площадью проходного сечения fi движется жидкость плотностью ρ с переменным во времени τ объемным расходом Q (τ), определяющим скорости течения W( τ ). Пересечение статических характеристик насоса - H (Q) и трассы циркуляции - H _С(Q) определяет рабочую точку системы а и величину установившейся подачи - Q _УСТ. Пренебрегая инерцией насоса, рассмотрим нестационарное поведение системы используя теорему об изменении кинетической энергии системы материальных точек. Наиболее удобной формулировкой теоремы для рассматриваемой задачи является:

 

, (13.1)

 

где: Е - кинетическая энергия потока жидкости в сети,

N –полезная мощность насоса,

N_С – мощность, рассеиваемая в контуре циркуляции при течении жидкости.

Кинетическая энергия потока складывается из кинетических энергий выделенных участков:

(13.2)

 

Полезная мощность насоса N _пол равна: N _пол = ρ Qg H (Q), а мощность сил трения N _Свыражаетсяаналогично потери напора трассы циркуляции H _С(Q): N _С = ρ Qg H _С(Q). Дифференцирование 13.2, подстановка вместе с N _пол и N _С в 13.1 приводит исходное уравнение 13.1 после преобразований к расчетному виду:

 

, (13.3)

 

где: .

Величину Q _УСТ при функционировании системы считать постоянной во времени можно лишь условно. Вследствие неизбежных возмущений в сети и работе насоса она непрерывно меняется, совершая колебания малой амплитуды Δ Q вблизи принимаемой за постоянную Q _УСТ. Если эти колебания не имеют развития во времени, то система обладает свойством устойчивости.

Для анализа устойчивости представим величину подачи (расхода) как сумму постоянной величины Q и по отношению к ней малой, но переменной во времени Δ Q (τ):

Q (τ) = Q + Δ Q (τ). (13.4)

 

Запись 13.3 с учетом 13.4 дает дифференциальное уравнение относительно Δ Q (τ):

 

. (13.5)

 

 

В уравнении 13.5 зависимость H [ Q+ Δ Q (τ)] и H _С[ Q+ Δ Q (τ)] представлена первыми членами разложения функций в ряд, причем производные в квадратных скобках, а, следовательно, и величина коэффициента В определяются характеристиками насоса и сети. Например, на рис. 13.1 производная от функции H (Q) отрицательна, а от H _С(Q) – положительна. Поэтому для этого примера во всем диапазоне изменения Q коэффициент В < 0.

Для определения вида функции Δ Q (τ) проинтегрируем уравнение с разделяющимися переменными 13.5 в рабочей точке, т.е. при фиксированном В. Разделяя переменные:

,

и интегрируя:

ln Δ Q (τ) = В τ + ln С,

получаем:

Δ Q (τ) = С ехр (В τ). (13.6)

 

Таким образом, поведение во времени отклонения Δ Q (τ) от установившегося Q _УСТ определяется знаком постоянной В. При В < 0 случайное малое отклонение Δ Q (τ)уменьшается во времени и система возвращается в исходное состояние, т.е. является устойчивой. Неустойчивая система (В > 0) будет в случаях:

- возрастающей H (Q), что возможно на начальном участке характеристики насоса или компрессора, имеющего РК с β ₂> 90⁰,

- падающей H _С(Q), иногда существующей в случае обогреваемых парогенерирующих каналов, входящих в контур циркуляции.

Для учета влияния насоса на устойчивость работы системы необходимо присоединить к 13.1 дифференциальное уравнение динамики насоса и проанализировать полученную систему вышеописанным образом.

Осевые насосы предназначены для работы с большими подачами и относительно низкими напорами; их коэффициент быстроходности n_S > 600. Они просты по конструкции и обладают достаточно высоким КПД.

Рабочее колесо осевой машины (насоса, вентилятора, компрессора) представляет собой втулку диаметра D _ВТ -1 с консольными лопастями – 2 и размещается в корпусе – 3 на вращающемся с угловой скоростью ω валу – 4 (рис. 13.2). В корпусе диаметром D размещены подшипниковые опоры – 5 и неподвижный направляющий аппарат НА. Перекачиваемая жидкость объемного расхода Q поступает к РК и отводится от него в осевом направлении вдоль цилиндрических поверхностей. РК при своем вращении отклоняет поток жидкости от осевого направления со скоростью С₁≥ С₀ в сторону окружной скорости лопастей. Это отклонение вызывает изменение количества движения и создает связанную с ним разность давлений после насоса и перед ним – Р ₅ - Р ₀. Для уменьшения гидравлических потерь путем перехода от спирального течения на выходе из РК (скорость С₂) к осевому (скорость С₄) обычно устанавливают осевой направляющий аппарат ОНА.

Полученная при испытаниях типичная характеристика высоконапорного осевого насоса P (Q), приведенная на рис. 13.2 имеет седлообразную форму, что объясняется снижением подъемной силы лопастей при малых подачах и наличием неизбежных вторичных течений через зазоры между корпусом и РК. Это заставляет устанавливать рабочую область характеристики в стабильной части правее P_МАХ, т.е. вне области резко выраженных максимальных КПД – η. Вследствие высокой быстроходности высота всасывания осевых насосов невелика и во избежание кавитации их часто выполняют погружными.

Для регулирования подачи осевых насосов применяются следующие, перечисленные в порядке возрастания энергетических потерь способы:

-оснащение поворотно-лопастным РК,

-иэменение угловой скорости вращения,

-установка ОНА перед РК,

-дросселирование.

 

 

 

 

 

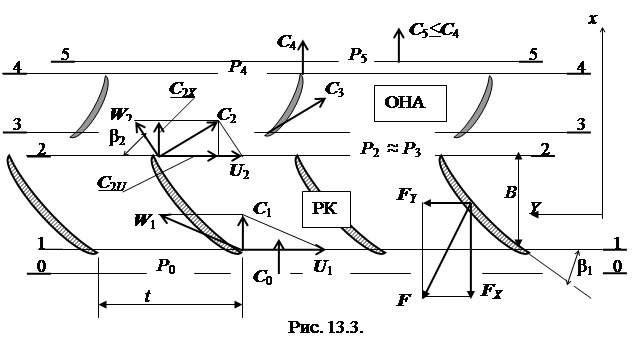
Теоретической основой расчета осевых насосов служит рассмотрение течения среды в решетке радиальных лопастей РК. Обычно эту решетку представляют в виде бесконечной прямой плоской решетки шириной B и шагом t, как это изображено на рис. 13.3. Схема соответствует развертке секущего цилиндра диаметром D _СЦ (D _ВТ < D _СЦ < D) на плоскость и содержит планы скоростей потока в сечениях 0-1-2-3-4-5. Планы скоростей изображены согласно геометрии проточной части, требованию безударного входа в МЛП (угол β ₁) и уравнения неразрывности. Обозначены распределение давления по ходу потока и проекции усилий F, действующих на лопасти. При отсутствии работы центробежных сил прирост давления потока происходит за счет преобразования кинетической энергии.

Уравнение Эйлера для анализируемой схемы определяет величину теоретического давления Р _Т через окружную скорость U = U ₁ = U ₂ и проекцию на ось х абсолютных скоростей С потока С_Х = С _{1 Х} = С _{2 Х} :

 

Р _Т= ρ U С_Х (Ctg β ₁ - Ctg β ₂). (13.7)

 

 

Сложность течения через решетку профилей и наличие специфических потерь в МЛП РК значительно снижают точность расчетов по теоретическим моделям, заставляя разработчиков широко применять экспериментальную отработку проектируемых осевых машин.