Формула полной вероятностиПусть событие A может произойти только вместе с одним из попарно несовместных событий H1, H2,..., Hn, образующих полную группу. Тогда, если произошло событие A, то это значит, что произошло одно из попарно несовместных событий H1A, H2A,..., HnA. Следовательно,
Применяя аксиому сложения вероятностей, имеем
Но
Эта формула называется формулой полной вероятности. События H1, H2,..., Hn часто называют «гипотезами». Пример. В магазин поступили электрические лампочки одного типа, изготовленные на четырех ламповых заводах: с 1-го завода 250 шт., со 2-го — 525 шт., с 3-го — 275 шт. и с 4-го — 950 шт. Вероятность того, что лампочка прогорит более 1500 часов, для 1-го завода равна 0, 15, для 2-го — 0, 30, для 3-го — 0, 20, для 4-го — 0, 10. При раскладке по полкам магазина лампочки были перемешаны. Какова вероятность того, что купленная лампочка прогорит более 1500 часов? Решение: Пусть A — событие, состоящее в том, что лампочка прогорит более 1500 часов, а Н1, Н2, Н3 и Н4 — гипотезы, что она изготовлена соответственно 1, 2, 3 или 4-м заводом. Так как всего лампочек 2000 шт., то вероятности гипотез соответственно равны
Далее, из условия задачи следует, что
Используя формулу полной вероятности (11), имеем
Предположим, что производится некоторый опыт, причем об условиях его проведения можно высказать n единственно возможных и несовместных гипотез Спрашивается, как изменятся вероятности гипотез, если стало известным, что событие А произошло? Иными словами, нас интересуют значения вероятностей На основании соотношений (4) и (5) имеем
откуда
Но по формуле полной вероятности
Поэтому
Формула (12) называется формулой Бейеса*.
Пример. На склад поступило 1000 подшипников. Из них 200 изготовлены на 1-м заводе, 460—на 2-м и 340 - на 3-м. Вероятность того, что подшипник окажется нестандартным, для 1-го завода равна 0, 03, для 2-го — 0, 02, для 3-го — 0, 01. Взятый наудачу подшипник оказался нестандартным. Какова вероятность того, что он изготовлен 1-м заводом? Решение: Пусть A — событие, состоящее в том, что взятый Подшипник нестандартный, а
Найдем
Таким образом, вероятность гипотезы, что подшипник изготовлен 1-м заводом, изменилась после того, как стало известно, что он нестандартен.
|



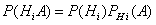 (i=1, 2,..., n), поэтому
(i=1, 2,..., n), поэтому



 , имеющих вероятности
, имеющих вероятности  . Пусть в результате опыта может произойти или не произойти событие А, причем известно, что если опыт происходит при выполнении гипотезы
. Пусть в результате опыта может произойти или не произойти событие А, причем известно, что если опыт происходит при выполнении гипотезы  , то
, то 

 .
.



 - гипотезы, что он изготовлен соответственно 1-м, 2-м или 3-м заводом. Вероятности указанных гипотез составляют
- гипотезы, что он изготовлен соответственно 1-м, 2-м или 3-м заводом. Вероятности указанных гипотез составляют

 , т. е. вероятность того, что подшипник, оказавшийся нестандартным, изготовлен 1-м заводом. По формуле Бейеса имеем
, т. е. вероятность того, что подшипник, оказавшийся нестандартным, изготовлен 1-м заводом. По формуле Бейеса имеем



