Двоичные операцииСложение и умножение. Начнем с очень простой арифметической задачи сложения двух двоичных целых чисел, например,
Предположим, что оба числа имеют длину в к бит. Если запись одного из чисел короче, ее можно дополнить нужным числом нулей слева. Детально проанализируем всю процедуру сложения. При сложении необходимо к раз повторить следующие шаги. Посмотреть на верхний и нижний биты, а также проверить, имеется ли перенос единицы от сложения младших разрядов. Если оба бита нулевые, а переноса нет, то в данном разряде суммы записываем нуль и двигаемся дальше. Если либо а) оба бита нулевые и есть перенос, либо б) один бит — нуль, другой — единица и переноса нет, то записываем единицу и двигаемся дальше. Если либо а) один бит — нуль, другой — единица и есть перенос, либо б) оба бита — единицы и переноса нет, то записываем нуль в данный разряд, записываем единицу переносов в следующий столбец и двигаемся дальше. Если оба бита — единицы и есть перенос, то в данном разряде суммы записываем единицу, записываем единицу переносов в следующий столбец и двигаемся дальше. Однократное выполнение этих шагов называется двоичной (битовой) операцией. Сложение двух k -разрядных двоичных чисел требует к двоичных операций. Мы увидим ниже, что и более сложные задачи тоже могут быть разбиты на двоичные операции. Время, которое расходует компьютер на решение задачи, по сути дела пропорционально числу двоичных операций. Конечно, константа пропорциональности — число наносекунд, расходуемых на одну двоичную операцию, — зависит от вида компьютера. (Сказанное является упрощением, так как это время может зависеть также от «технических» факторов, например, времени доступа к памяти.) Когда мы говорим об оценке времени работы, подразумевается оценка числа двоичных операций. В этих оценках мы будем пренебрегать временем, расходуемым на запись информации или на логические шаги, отличные от двоичных операций. Теперь рассмотрим процесс умножения k -разрядного двоичного числа на l -разрядное двоичное число. Например,
Предположим, что мы пользуемся обычным способом умножения k -разрядного двоичного числа п и l -разрядного двоичного числа т. Мы получаем самое большее l строк (каждый нулевой бит числа m уменьшает это количество на единицу), где каждая строка содержит копию числа n, сдвинутую влево на некоторое расстояние, т. е. копию, дополненную нулями справа. Пусть имеется l1 ≤ l строк. Поскольку мы ограничиваемся двоичными операциями, мы не можем сложить все строки сразу. Правильнее будет двигаться от второй строки к l1 -й, складывая каждую строку с накопившейся суммой верхних строк. На каждом этапе сначала отмечаем, как далеко сдвинуто влево число n в рассматриваемой строке. Сносим вниз крайние правые разряды накопленной суммы верхних строк, а остальную часть записи накопленной суммы складываем (описанным выше способом) с числом n, что требует к двоичных операций. В примере выше 11101× 1101 после сложения первых двух строк получаем 10010001, сносим вниз последние три разряда 001 и складываем остальное (т.е. 10010) с n = 11101. И наконец, к сумме 10010+ 11101 = 101111 приписываем 001 и получаем 101111001 — сумму l1 = 3 строк. Это описание показывает, что задача умножения может быть разложена на l1 -1сложений, по к двоичных операций каждое. Так как l1 -1 < l ≤ l, то получаем простую оценку Time (умножение k -разрядного и l- разрядного двоичных чисел) < kl. Здесь и далее Time (A) обозначает число двоичных операций, необходимых для выполнения процедуры А. Замечания. Во-первых, как упоминалось выше, мы подсчитали только число двоичных операций. Мы пренебрегли временем на сдвиг числа n влево и временем на снос крайних правых разрядов накопленной суммы. На практике операции сдвига и копирования являются быстрыми по сравнению с большим числом производимых двоичных операций, так что можно без опаски проигнорировать их. Другими словами, мы определим «временную оценку (сложности)» арифметической задачи как верхнюю границу для числа двоичных операций без учета операций сдвига, копирования, обращения в память и т.п. Мы могли бы применить эту же временную оценку к умножению k-разрядной и l -разрядной двоичных дробей. Единственное отличие состоит в необходимости правильного определения места для запятой, разделяющей целую и дробную части. Во-вторых, если мы хотим получить простую и удобную в работе оценку, мы всегда должны предполагать, что имеем дело с «самым плохим случаем». Например, если двоичное разложение числа m имеет много нулей, то l1 будет значительно меньше l. Поэтому можно использовать оценку Time (умножение k -разрядного и l -разрядного двоичных чисел) < k (k-число единиц в двоичном разложении m). Однако обычно вместо такого уточнения (понижения) нашей временной оценки удобнее пользоваться простой равномерной оценкой, зависящей лишь от длины записи n и m, а не от конкретных значений битов. Как частный случай, имеем оценку: Time (умножение двух k -разрядных двоичных чисел) < k2. Наконец, наша оценка kl может быть выражена в терминах n и m, если вспомнить приведенную выше формулу для числа разрядов, из которой следует, что Пример 1. Найти верхнюю границу для числа двоичных операций, необходимых для вычисления n! Решение. Используем следующую процедуру. Сначала умножим 2 на 3, затем результат умножим на 4, новый результат умножим на 5 и т. д., пока не получим n!. На (j - 1)-м шаге (j = 2, 3,..., п — 1) производится умножение j! на (j +1). Поэтому есть п-2 шагов, каждый из которых состоит в умножении частичного произведения j! на очередное целое число. Частичные произведения быстро станут очень большими. В качестве оценки для числа разрядов частичного произведения в наихудшем случае возьмем число разрядов последнего произведения, т.е. числа n! При определении числа двоичных разрядов в произведении мы используем тот факт, что это число не превосходит суммы числа разрядов у сомножителей. Следовательно, произведение п целых k -разрядных чисел имеет не более пк разрядов. Таким образом, если n - двоичное k -разрядное число (тогда любое меньшее число имеет не больше к разрядов), то п! имеет самое большее пк разрядов. Итак, в каждом из n-2 умножений, необходимых при вычислении п!, мы умножаем не более чем k -разрядное целое число j + 1 на не более чем nk -разрядное целое число j!. Это требует самое большее пк двоичных операций. Всего таких умножений п-2. Поэтому общее число двоичных операций ограничено величиной
Вычитание и деление. Существуют две другие арифметические операции — вычитание и деление — имеют те же самые оценки временной сложности, что сложение и умножение соответственно: Time (вычитание к-разрядного двоичного числа из l -разрядного) ≤ max (k, l), Time (деление k -разрядного двоичного числа на l -разрядное) ≤ kl. Более точно, для описания вычитания надо расширить круг двоичных операций, включив в него операцию вычитания нуля или единицы из других нуля или единицы, возможно, с займом единицы из старшего разряда (см. пример 2). Анализируя деление в двоичной системе. Пусть к ≥ l (если к < l деление тривиально, т.е. частное равно нулю, а все делимое образует остаток). Нахождение частного и остатка требует самое большее k - l +1вычитаний. Каждое вычитание требует l или l + 1 двоичных операций, но в последнем случае в самом левом разряде разности будет стоять нуль, поэтому можно опустить одну двоичную операцию (считая, что это скорее операция «по учету данных», а не вычисление). Подобным образом мы игнорируем и другие технические детали, например, сравнение двоичных целых чисел (при определении минимального числа разрядов делимого, которые образуют число, большее делителя), снос разрядов и т.п. Таким образом, наша оценка есть просто (k - l +1) l, что не больше kl. Пример 2. Найти верхнюю границу для числа двоичных операций, необходимых для вычисления биномиального коэффициента Решение. Так как Теперь обсудим весьма удобное обозначение для краткой записи временных оценок сложности. (А.В.Черемушкин, 2002)
|


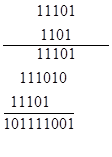
 и
и 
 , что приблизительно равно
, что приблизительно равно 
 , то без потери общности можно предположить, что
, то без потери общности можно предположить, что  . Будем использовать следующую процедуру вычисления
. Будем использовать следующую процедуру вычисления  . Мы имеем m -1умножений и последующие m -1делений. Каждый раз максимально возможная величина первого числа при умножении и делении есть
. Мы имеем m -1умножений и последующие m -1делений. Каждый раз максимально возможная величина первого числа при умножении и делении есть  , а граница для второго числа есть п. Рассуждая аналогично примеру 1, убеждаемся в том, что граница для общего числа двоичных операций есть
, а граница для второго числа есть п. Рассуждая аналогично примеру 1, убеждаемся в том, что граница для общего числа двоичных операций есть  , что при больших n и m приблизительно равно
, что при больших n и m приблизительно равно  .
.


