Экстремумы функцииЭкстремумами функции называются ее максимумы и минимумы. Точка х0 называется точкой максимума функции При этом число
Понятие экстремума связано с наличием окрестности точки х0 из области определения функции. Поэтому функция может иметь экстремум лишь во внутренних точках области определения.
Необходимое условие экстремума. Если непрерывная функция
Необходимое условие экстремум не является достаточным, т.е. точки, в которых
Точки, в которых необходимое условие экстремумов выполняется, называются критическими, или подозрительными на экстремум. Критические точки входят в область определения функции вместе с некоторой своей окрестностью, в которой функция является непрерывной и дифференцируемой (за исключением, быть может, самой критической точки, где
Первый достаточный признак экстремума. Если при переходе через критическую точку х0 (слева направо) производная Второй достаточный признак экстремума. Пусть х0 – стационарная точка Первый достаточный признак экстремума функции Если если если
Пример 1. Найти экстремумы функции Решение. Находим Так как функция и ее производная определены и непрерывны при хÎ (-¥; +¥), то критическими точками являются только точки, в которых
На основании первого достаточного признака экстремумов делаем вывод, что данная функция имеет три точки экстремумов: x = –2 и х = 2 – точки минимумов, х = 0 – точка максимума.
ymin = y(–2) = –1; ymax = y(0) = 3; ymin = y(2) = –1; В данной задаче все критические точки являются стационарными Так как так как так как Ответ:
Пример 2. Найти экстремумы функции
Решение. Область определения функции хÎ (–¥; +¥). Вычисляем производную Находим точки, в которых выполняется необходимое условие экстремумов:
Получились две критические точки, причем, вторая из них (х = 0) является подозрительной на острый экстремум. Проверяем достаточное условие монотонности функции и экстремумов (первое):
x = –1 – точка max; х = 0 – точка min (острого);
Ответ:
Пример 3. Исследовать функцию на монотонность и экстремумы Решение. Область определения функции: х ¹ 1. Находим производную
Необходимое условие экстремумов:
Достаточное условие монотонности и экстремумов:
Вычисляем значения функции в точках экстремумов:
Строим схематический чертеж по результатам исследования:
Ответ:
Пример 4. Найти экстремумы функции
Решение. Область определения функции: х > 0. Находим производную Необходимое условие экстремумов:
Таким образом,
Ответ:
Дополнительные упражнения.
Ответы.
|

 , если существует такая двухсторонняя окрестность точки х0, что для всякой точки х ¹ х0 этой окрестности выполняется неравенство
, если существует такая двухсторонняя окрестность точки х0, что для всякой точки х ¹ х0 этой окрестности выполняется неравенство  .
. называется максимумом функции
называется максимумом функции 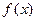 . Аналогично, если для всякой точки х ¹ х0 из некоторой окрестности точки х0 выполняется неравенство
. Аналогично, если для всякой точки х ¹ х0 из некоторой окрестности точки х0 выполняется неравенство  , то х0 называется точкой минимума, а число
, то х0 называется точкой минимума, а число  – минимумом функции
– минимумом функции  или же
или же  не существует, не обязательно являются точками экстремумов функции.
не существует, не обязательно являются точками экстремумов функции. может не существовать). Критические точки, в которых
может не существовать). Критические точки, в которых  не существуют, являются подозрительными на острый экстремум функции
не существуют, являются подозрительными на острый экстремум функции  изменяет свой знак, то в точке х0 есть экстремум причем, это максимум, если знак
изменяет свой знак, то в точке х0 есть экстремум причем, это максимум, если знак  , непрерывная в точке х0.
, непрерывная в точке х0. .
. .
. , т.е. х1=0, х2, 3=±2. Эти точки разбивают область определения функции на интервалы знакопостоянства ее производной (следовательно, на интервалы монотонности функции):
, т.е. х1=0, х2, 3=±2. Эти точки разбивают область определения функции на интервалы знакопостоянства ее производной (следовательно, на интервалы монотонности функции):
 Вычисляя значение функции в точках экстремумов, находим экстремумы функции и строим схематически график:
Вычисляя значение функции в точках экстремумов, находим экстремумы функции и строим схематически график: , поэтому можно проверять в них и второе достаточное условие экстремумов. Для этого находим
, поэтому можно проверять в них и второе достаточное условие экстремумов. Для этого находим 
 то х = –2 – точка минимума,
то х = –2 – точка минимума, то х = 0 – точка максимума,
то х = 0 – точка максимума, то х = 2 – точка минимума.
то х = 2 – точка минимума.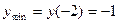 ;
;  ;
;  .
.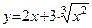 .
. .
. Û х = –1;
Û х = –1;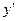 не существует, елси
не существует, елси  Û х = 0.
Û х = 0.

 ;
; .
. .
.



 Þ х1 = 0, х2 = 2 – это стационарные точки
Þ х1 = 0, х2 = 2 – это стационарные точки
 – точка max,
– точка max,  – точка min.
– точка min. ;
; .
.


 возрастает при хÎ (-¥; 0) и (2; +¥),
возрастает при хÎ (-¥; 0) и (2; +¥), .
.
 .
. Þ
Þ  Þ
Þ  ;
; =
=  Þ
Þ  Þ
Þ  =
=  =
=  .
. =
=  ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
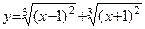 ;
;
 ;
;
 ;
;
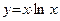 .
.
 ;
;
 ;
;
 ;
;
 ;
;
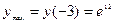 ;
;
 ;
;
 ;
;



 ;
;

 .
.



