Наибольшее и наименьшее значения функцииЕсли функция
Эти значения достигаются функцией либо в точках экстремумов внутри отрезка, либо на концах отрезка.
Правило практического нахождения наименьшего и наибольшего значений функции на отрезке 1) найти критические точки функции на интервале 2) вычислить значения функции в найденных критических точках; 3) вычислить значения функции на концах отрезка, то есть в точках х = a и х = b; 4) среди всех вычисленных значений функции выбрать наибольшее и наименьшее. Если функция
Пример 1. Найти наибольшее и наименьшее значение функции
Решение. Так как
заключаем, что наименьшее значение функции равно 1 и достигается в точке х = –2 и х = 1, а наибольшее значение функции равно 21 и достигается в точке х = 3. Все полученные результаты хорошо иллюстрируются схематичным графиком на заданном отрезке.
Ответ:
Пример 2.
Решение. Во всех точках заданного замкнутого отрезка данная функция определена и непрерывна, имеет производную
Обе стационарные точки х1 = 0 и х2
Схема графика функции:
Ответ:
Пример 3. Найти наименьшее и наибольшее значения функции
Решение. На данном замкнутом отрезке функция является непрерывной и имеет производную Находим критические точки внутри заданного промежутка:
Þ только х1 = Вычисляем значения функции в критических точках и на концах промежутка:
Схема графика функции:
Ответ:
Во многих геометрических, физических и технических задачах требуется найти наибольшее и наименьшее значение величины, связанной функциональной зависимостью с другой величиной. Для решения такой задачи следует, исходя из её условия, выбрать независимую переменную и выразить исследуемую величину через эту переменную, а затем найти искомое наибольшее или наименьшее значение полученной функции. При этом промежуток изменения независимой переменной может быть конечным или бесконечным, он также определяется из условия задачи.
Пример 4. Определить размеры открытого бассейна с квадратным дном объемом 32 м3 так, чтобы на облицовку его стен и дна пошло наименьшее количество материала.
Решение.
Количество материала, необходимого для облицовки стен и дна бассейна определяется площадью поверхности бассейна, т.е. величиной х – это длина стороны квадратного дна, y – это высота бассейна.
Так как объем бассейна фиксирован Тогда, подлежащая исследованию величина площади
Исследуем эту функцию на наименьшее значение, построив график ее зависимости от х:
S(4) =Smin = 16+ Таким образом, Sнаим = Smin = S(4) = 80, т.е. х = 4 Þ Ответ: размеры бассейна х = 4 м, y = 2 м.
Пример 5. Из трех досок одинаковой ширины сколачивается желоб для подачи воды. При каком угле
Решение.
Поперечное сечение желоба представляет собой равнобочную трапецию ABCD, у которой боковые стороны и нижнее основание равны ширине досок (обозначим ее через a). Очевидно, что площадь этой трапеции зависит от угла наклона Тогда Исследуемую величину площади трапеции S запишем как функцию угла
Найдем наибольшее значение этой непрерывной функции на замкнутом промежутке:
Û Û
Проверим, что это точка максимума с помощью второй производной:
при Так как этот максимум является единственным экстремумом на промежутке, то он и дает наибольшее значение функции Найдя Ответ:
Дополнительные упражнения.
Найти наименьшее и наибольшее значение функции на замкнутом отрезке.
6. Число 66 представить в виде суммы двух положительных слагаемых так, чтобы их произведение было наибольшим.
7. В треугольник с основанием а и высотой h вписан прямоугольник, основание которого лежит на основании треугольника, а две вершины – на боковых сторонах. Найти наибольшую площадь вписанного прямоугольника.
8. Найти размеры цилиндрической закрытой цистерны с заданным объемом
9. Расходы на топливо судна состоят из двух частей. Первая часть пропорциональна кубу скорости судна и при скорости в 10 км/час составляет 30 рублей в час. Вторая часть расходов не зависит от скорости и составляет 480 рублей в час. При какой скорости судна общая сумма расходов на 1 км пути будет наименьшей? Чему равна при этом общая сумма расходов за 1 час?
1. 2. 3. 4. 5. 6. 33+33; 7. 8. 9.
|

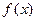 непрерывна на замкнутом отрезке xÎ [a; b], то она обязательно имеет на этом отрезке наименьшее и наибольшее значения (это одно из свойств функций, непрерывных на замкнутом отрезке):
непрерывна на замкнутом отрезке xÎ [a; b], то она обязательно имеет на этом отрезке наименьшее и наибольшее значения (это одно из свойств функций, непрерывных на замкнутом отрезке): ,
, .
. :
: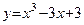 на отрезке хÎ [–2; 3].
на отрезке хÎ [–2; 3].
 , то критическими точками функции являются х1 = –1 и х2 = 1 и они обе принадлежат отрезку
, то критическими точками функции являются х1 = –1 и х2 = 1 и они обе принадлежат отрезку  5,
5,  1,
1, 1,
1,  21,
21,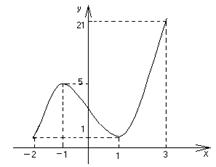
 ,
,  .
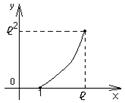
. , хÎ [1; е]. Найти
, хÎ [1; е]. Найти  и
и  .
.

 , если
, если 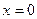 или
или  .
. не принадлежат отрезку [ 1; е ]. Поэтому, внутри заданного отрезка нет критических точек (то есть функция на нем сохраняет монотонность). Остается вычислить значение функции на концах отрезка:
не принадлежат отрезку [ 1; е ]. Поэтому, внутри заданного отрезка нет критических точек (то есть функция на нем сохраняет монотонность). Остается вычислить значение функции на концах отрезка: ,
,  .
.
 ,
,  .
. ,
,  .
.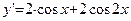
 .
. Þ
Þ  Û
Û  Û
Û
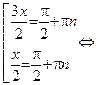

 и х2 = p принадлежат
и х2 = p принадлежат  .
.



 ;
;
 ;
;

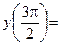
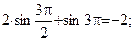

 ,
,  .
.
 (м2), где
(м2), где , то величины х и y не являются независимыми, а связаны между собой равенством x2y=32, из которого находим
, то величины х и y не являются независимыми, а связаны между собой равенством x2y=32, из которого находим 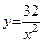 .
. , выражается как функция одной независимой переменной х:
, выражается как функция одной независимой переменной х:
 , хÎ (0; +¥).
, хÎ (0; +¥). Þ
Þ  при х = 4;
при х = 4;

 (m2).
(m2).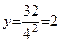 .
. наклона боковых стенок к днищу желоба площадь поперечного сечения желоба будет наибольшей?
наклона боковых стенок к днищу желоба площадь поперечного сечения желоба будет наибольшей?
 .
.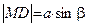 ,
,  ,
, 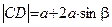 .
. :
: Þ
Þ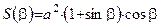 ,
,  Î
Î 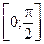 , причем, S(0) = а2, S
, причем, S(0) = а2, S  = 0.
= 0. Þ
Þ при
при  Û
Û  Û
Û Û
Û 


 – единственная стационарная точка из промежутка
– единственная стационарная точка из промежутка 
 Þ
Þ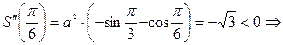
 функция
функция  имеет максимум (по второму достаточному условию экстремумов).
имеет максимум (по второму достаточному условию экстремумов). .
. .
. , хÎ
, хÎ  ;
;
 , хÎ
, хÎ  ;
;
 , хÎ
, хÎ  ;
;
 , хÎ
, хÎ  ;
;
 , хÎ
, хÎ  и с наименьшей площадью полной поверхности.
и с наименьшей площадью полной поверхности. ;
; ;
;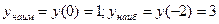 ;
; ;
;
 ;
; ;
; .
.


