Корреляционный анализ. Функция автокорреляцииЕще одним методом выделения аномального эффекта является корреляционный анализ. Корреляционный анализ — метод обработки данных, заключающийся в изучении коэффициентов корреляции между переменными. При этом сравниваются коэффициенты корреляции между одной парой или множеством пар признаков, для установления между ними статистических взаимосвязей. В данной работе для определения аномального эффекта буде применятся функция автокорреляции. Автокорреляционная функция (АКФ) показывает связь сигнала с копией самого себя, смещенной на величину τ. АКФ описывается интегралом:
Механизм определения аномального эффекта в данной работе принципиально не отличается от механизма, описанного в работе 2. Это означает, что, прежде всего необходимо выделить региональный фон. Для определения регионального фона необходимо рассчитать функцию автокорреляции для модельного сигнала, определить радиус корреляции и провести осреднение исходного сигнала скользящим окном, кратным радиусу корреляции. Прежде чем начать расчет АКФ, из модельного сигнала необходимо удалить математическое ожидание m. Его можно определить по следующей формуле:
где Fi(t) – значения функции, N – общее количество значений функции. После удаления из сигнала математического ожидания необходимо рассчитать АКФ, используя формулу 13 и определить радиус корреляции. Радиус корреляции может быть определен графически. Для этого необходимо отнормировать значения АКФ и построить график по нормированным значениям. Для нормирования используется следующая формула:
где fn – нормированное значение функции, fi – текущее значение функции, а fmax – максимальное значение функции. Радиус корреляции определяется по первому пересечению линии Y= 0.1*fnmax и графика нормированной АКФ. Пример определения радиуса корреляции приведен на рисунке 9.
Рис. 9
После определения радиуса корреляции необходимо подобрать размер скользящего окна для осреднения. Подбор производится экспериментальным путем. Исходный сигнал усредняется сначала окном равным двум радиусам корреляции R, а затем размер окна увеличивается, до тех пор, пока полностью не сгладится аномальный эффект, как показано на рисунке 10. После сглаживания аномального эффекта, полученный график и представляет собой региональный фон. После выделения регионального фона необходимо воспользоваться формулой 11 и определить аномальный эффект. График аномальных значений представлен на рисунке 11. Как видно, полученный аномальный эффект несколько отличается от того, что был получен ранее (рис. 6), тем не менее, оба эффекта имеют достаточно выраженные сходные черты, а значит характер аномалии сохраняется. Сравнением аномальных эффектов, полученных в работах 2 и 4 можно руководствоваться для проверки правильности вычислений.
Рис. 10
Рис. 11
Задание. 1. Используя данные, ранее выполненных работ, рассчитать АКФ для модельного сигнала. 2. Определить радиус корреляции 3. Провести подбор размеров скользящего окна и провести сглаживание исходного сигнала. 4. Рассчитать аномальный эффект. Лабораторная 5.
|

 [13]
[13] [14]
[14]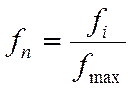 [15]
[15]





