Электрические цепи постоянного тока
Предисловие
Электрическая энергия – энергия электромагнитного поля, представляющая один из видов материи. Её потребителями на сегодняшний день являются промышленные предприятия, транспорт, сельское хозяйство, объекты коммунально-бытового назначения и строительства. Выработанная различными источниками, она расходуется на электропривод, электрохимические и электротермические установки, на электрическое освещение, а также на электросвязь и вычислительную технику. Электрическая энергия перед другими видами энергии обладает рядом преимуществ: универсальностью, так как легко преобразуется в другие виды энергии; экономичностью передачи электроэнергии на большие расстояния; простотой распределения между различными потребителями. Преимущества генерирования, передачи, распределения и преобразования электрической энергии, обеспечили широкое применение ее в электротехники. Основными энергосберегающими направлениями электрической энергии при потреблении являются: - сокращение всех видов потерь электроэнергии; - переход на энергосберегающие технологии; - совершенствование, реконструирование, создание новых энергетических установок; - внедрение автоматического и автоматизированного управления технологическими устройствами. Будущие инженеры – механики и электромеханики обязаны получить представление о современных способах получения электроэнергии, развитии систем электроснабжения на транспорте и в промышленных объектах, а также об используемом в них электрооборудовании; должны изучить устройства, принцип работы, эксплуатационные характеристики, области применения, достоинства и недостатки электротехнических установок и электрооборудования; освоить методы расчета электрических цепей и устройств, способы рационального расходования электроэнергии при работе электрооборудования; изучить электротехническую символику и терминологию, чтобы уметь находить общий язык с представителями подрядных и субподрядных организаций и электриками, работающими на транспорте и в других отраслях хозяйства. Учебное пособие предназначено для студентов вузов, изучающих курс электротехники и электроники на механических и электромеханических специальностях. Материал учебного пособия может быть использован при освоении студентами последующих прикладных дисциплин и при решении практических задач.
Электрические цепи постоянного тока
Электрическая цепь представляет собой совокупность электротехнических устройств, создающих путь для электрического тока, электромагнитные процессы в которых описываются уравнениями с учетом понятий об электродвижущей силе, электрическом токе и электрическом напряжении. Основными элементами электрической цепи (рис.1.1) являются источники и потребители электрической энергии. R1 R2
r o
Рис.1.1
В качестве источников электрической энергии постоянного тока широко распространены генераторы постоянного тока и гальванические элементы. Источники электрической энергии характеризуются электродвижущей силой (ЭДС), обозначаются буквой Е, а реальный источник обладает внутренним сопротивлением ro. Потребителями электрической энергии постоянного тока являются резисторы (для данной схемы R1, R2), электрические двигатели, электролизные ванны, электрические лампы и т.д. В электрической цепи за положительное направление ЭДС принимается направление, совпадающее с силой, действующей на положительный заряд, то есть от «-» источника к «+» источника. За положительное направление тока I принято направление, совпадающее с перемещением положительных зарядов, то есть от «+» к «-» источнику (рис.1.1). В электрической цепи ЭДС источника может иметь одинаковые с током направления, в этом случае источник ЭДС работает в режиме генератора и является источником электрической энергии, при этом ЭДС оказывается больше напряжения на его зажимах (Е > U). При направлении ЭДС в цепи противоположно току, источник становится потребителем электрической энергии, работающим в режиме потребителя, при этом Е < U на величину внутреннего падения напряжения roI. При расчетах электрических цепей, реальные источники электрической энергии заменяются схемами замещения. Для участка цепи, не содержащего источника энергии, связь между током I и напряжением U определяется законом Ома для участка цепи (рис.1.2).
1 R1 R2 2 R1 E R2 R3
φ 1 φ 2 φ 1 Рис.1.2 Рис.1.3
где φ 1 и φ 2 – потенциалы точек 1 и 2 цепи (причем φ 1 > φ 2); U 12 – напряжение (разность потенциалов φ 1 и φ 2) между точками 1-2;
где r o – внутреннее сопротивление источника энергии. Взаимосвязь между всеми видами мощностей в электрической цепи (баланс мощностей) определяется из уравнения:
где
Резисторы, а также сопротивления других электротехнических устройств, являются потребителями электрической энергии. Баланс мощностей определяется законом сохранения энергии, при этом в любой замкнутой электрической цепи алгебраическая сумма мощностей источников энергии равна алгебраической сумме мощностей, расходуемых потребителями электрической энергии. Электрическая цепь называется линейной, если она содержит только линейные элементы. Сопротивление линейного элемента всегда остается постоянным независимо от значений и направлений тока в нем и напряжения на его выводах. При расчете электрических цепей очень часто необходимо определить токи, напряжения и мощности на всех ее участках при заданных ЭДС источников и сопротивлений участков цепи. Такой расчет основан на применении законов Кирхгофа. При постоянных токах в цепи ни в одной из ее точек не могут накапливаться электрические заряды, так как это вызвало бы изменение потенциалов точек цепи и напряжений на участках. Следовательно, электрические заряды, притекающие к какому-либо узлу по одной части присоединенных к нему ветвей или проводов в единицу времени, равны зарядам, оттекающим от этого узла по другой части ветвей или проводов за ту же единицу времени. Это положение выражает первый закон Кирхгофа, который формулируется так: сумма токов, направленных к узлу, равна сумме токов, направленных от узла (рис.1.4). Или: алгебраическая сумма токов в узле электрической цепи равна нулю.
Σ Ι а = 0 или Ι 1 + Ι 2 – I 3 – Ι 4 = 0 (1.4)
R 1 E1
I4
R 4 E2 I2 I4
Рис.1.5
Второй закон Кирхгофа гласит: алгебраическая сумма ЭДС, действующих в любом контуре разветвленной цепи, равна алгебраической сумме падений напряжений на всех активных сопротивлениях этого контура (рис.1.5). Σ E = Σ I R (1.5)
Методика составления уравнения по второму закону Кирхгофа состоит в следующем: задается направление обхода в контуре, если направление ЭДС и направление тока на участке цепи совпадают с направлением обхода, тогда в уравнении ставится знак «плюс», не совпадают – знак «минус», следовательно, выражение 1.5 примет вид:
Е 1 – Е 2 = I 1 R 1 - I 2 R 2 - I 3 R 3 + I 4 R 4
|






 + I
+ I




 UR1 UR2
UR1 UR2 E
E _
_
















 φ 2
φ 2 ,
,  (1.1)
(1.1) R – арифметическая сумма сопротивлений на участке цепи. Для участка цепи, содержащей источник энергии (рис.1.3), закон Ома запишется в виде:
R – арифметическая сумма сопротивлений на участке цепи. Для участка цепи, содержащей источник энергии (рис.1.3), закон Ома запишется в виде: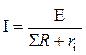 , (1.2)
, (1.2) , (1.3)
, (1.3) – алгебраическая сумма мощностей источников энергии (
– алгебраическая сумма мощностей источников энергии ( );
); алгебраическая сумма мощностей потребителей (полезная мощность (
алгебраическая сумма мощностей потребителей (полезная мощность ( );
); – суммарная мощность, обусловленная потерями в сопротивлениях источника (
– суммарная мощность, обусловленная потерями в сопротивлениях источника (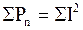 r o).
r o).
 I1 I3
I1 I3




