Формула КлоссаКогда речь идет о системах управления двигателем, важную роль играет аналитическая зависимость момента от скольже- Используя уравнение для определения
Отношение текущего момента к максимальному значению
Критическое скольжение:
тогда
В асинхронных двигателях без дополнительного сопротивления в цепи ротора можно приравнять сопротивление В этом случае, пока нет возможности более точно определить отношение
Пренебрегая значениями
Таким образом, получена формула Клосса, описывающая механическую характеристику асинхронного двигателя. 6.15. Эквивалентная схема замещения В отличие от трансформатора, который преобразует электрическую энергию одного напряжения в электрическую энергию другого напряжения, асинхронный двигатель преобразует электрическую энергию в механическую. При изменении нагрузки напряжение на зажимах машины остается неизменным. Практически неизменными остаются магнитный поток и ЭДС. Приведенная схема замещения в общем случае неудобна для изучения процессов, происходящих в машине. Эквивалентная схема, в которой намагничивающая цепь приведена к входным зажимам и в которой намагничивающий ток при всех возможных изменениях нагрузки и изменении скольжения постоянен, наиболее удобна. Найдем ток основной цепи преобразованной схемы как геометрическую сумму основного тока
где
где Полученной формуле соответствует эквивалентна схема, представленная на рис. 6.33.
Рис. 6.33
Ток основной части представленной эквивалентной схемы
Связь между токами
Так как
Пренебрегая последним слагаемым, получаем:
В реальных машинах
Таким образом, скорректированная схема замещения включает в себя полное сопротивление первичной и вторичной цепи, увеличенной
|

 , с помощью которой и данных каталога можно найти величину номинального момента, номинального скольжения, способность к перегрузкам и максимальный момент.
, с помощью которой и данных каталога можно найти величину номинального момента, номинального скольжения, способность к перегрузкам и максимальный момент.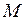 и
и  :
: ;
; .
.
 ,
,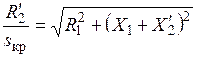 ;
; ,
,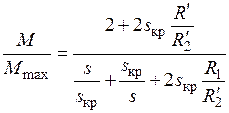 .
. приведенному сопротивлению ротора (
приведенному сопротивлению ротора ( ).
).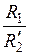 , можно записать
, можно записать .
. и
и  , получаем:
, получаем: .
. и тока идеального холостого хода
и тока идеального холостого хода  эквивалентной схемы двигателя (рис. 6.33)
эквивалентной схемы двигателя (рис. 6.33) ;
; ,
, - постоянная;
- постоянная;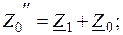

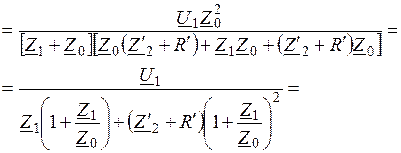
 .
. ,
, ,
,  ,
, 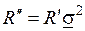 .
.

 .
. и
и  выражается уравнением:
выражается уравнением: .
. , коэффициент коррекции можно выразить следующей формулой:
, коэффициент коррекции можно выразить следующей формулой: .
.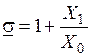 .
. . Пренебрегая, что
. Пренебрегая, что  , можно написать:
, можно написать: ;
; ;
; .
. Рис. 6.34
Рис. 6.34
 и
и  раз
раз 


