УСТОЙЧИВОСТЬРекомендуемая литература Александров А. В., Потапов В. Д., Державин Б. П. Сопротивление материалов. М.: Высш. шк., 1995. Гл. 15. Гастев В. А. Краткий курс сопротивления материалов. М.: Физматгиз, 1977. Гл. 12 (§ 49–51). Дарков А. В., Шпиро Г. С. Сопротивление материалов. М.: Высш. шк., 1989. Гл. 13. Основные понятия и формулы При расчете простейших стержневых систем мы научились удовлетворять двум важным требованиям, предъявляемым к конструкциям: требованиям прочности и жесткости стержневой системы. Любая конструкция должна удовлетворять еще одному важному условию, а именно условию устойчивости. Об условии устойчивости сжатых стержней конструкции и пойдет речь в данном разделе.
Положение равновесия стержня может быть устойчивым, неустойчивым и безразличным. Чтобы на опыте выявить, каким является равновесие стержня, надо вывести его из положения равновесия, приложив к стержню кратковременную малую возмущающую нагрузку, и посмотреть, как будет вести себя стержень после снятия возмущения. Рассмотрим центрально-сжатый стержень (рис. 6.1, а). Приложим к нему возмущающую нагрузку (сила f на рис. 6.1, б). При действии возмущающей нагрузки рассматриваемый стержень изогнется. Если после снятия возмущения стержень возвращается в исходное прямолинейное состояние, то это состояние называется устойчивым. Если же после удаления возмущающей нагрузки стержень остается в изогнутом состоянии, то первоначальная прямолинейная форма равновесия является неустойчивой. Нагрузка, при которой первоначальная форма равновесия становится неустойчивой, называется критической. Рис. 6.1, в, г поясняют данное определение критической силы. Если нагрузка меньше критической силы (см. рис. 6.1, в), то после прекращения действия возмущающей нагрузки стержень остается прямолинейным. Если же нагрузка достигла критической величины или стала больше (см. рис. 6.1, г), то стержень после снятия возмущения остается в изогнутом состоянии. Поскольку на практике всегда бывают какие-то возмущения, то при достижении силой критического значения сжатый стержень начинает изгибаться. Описанное явление носит название потери устойчивости центрально-сжатого стержня. Условие, обеспечивающее определенный запас против потери устойчивости стержней конструкции, называется условием устойчивости. Студент должен: ·* научиться находить величину критической нагрузки; ·* уметь обеспечить выполнение условий устойчивости и прочности, то есть вычислять допускаемую нагрузку или подбирать размеры поперечных сечений стержней так, чтобы была невозможна потеря устойчивости и прочности; ·* уметь определять нормируемый или действительный коэффициенты запаса устойчивости. Нормируемый коэффициент запаса устойчивости показывает во сколько раз критическая нагрузка превышает допускаемую, найденную из условия устойчивости. Величина нормируемого коэффициента запаса устойчивости не является постоянной величиной, а зависит от размеров стержня. Действительный коэффициент запаса устойчивости равен отношению критической нагрузки к действующей на стержень сжимающей силе. Определение критической нагрузки. Перед отысканием критической силы надо найти величину гибкости стержня
где l – длина стержня; В зависимости от величины · если
· если
· если
Величины
Условия устойчивости и прочности. Условием устойчивости центрально-сжатого стержня является условие
где Из условия устойчивости (6.6), если известны размеры сечения, можно найти значение допускаемой нагрузки
либо, если задана нагрузка F, определить площадь сечения А стержня. Однако найти сразу площадь А из условия устойчивости (6.6) нельзя, так как в этом условии коэффициент Для центрально-сжатых стержней малой и средней гибкости более опасным, чем условие устойчивости, может оказаться условие прочности, которое записывается в таком виде:
Здесь Определение коэффициента запаса устойчивости. Нормируемый коэффициент запаса устойчивости определяется по формуле
где допускаемая нагрузка находится из условия устойчивости (6.7). Обычно нормируемый коэффициент запаса устойчивости больше, чем нормируемый коэффициент запаса прочности, и для пластичных материалов находится в пределах Действительный коэффициент запаса устойчивости
где F – действующая на стержень сжимающая сила. Действительный коэффициент запаса устойчивости не должен быть меньше нормируемого, в оптимальном случае (для стержней с экономичным расходом материала) – равен нормируемому.
|

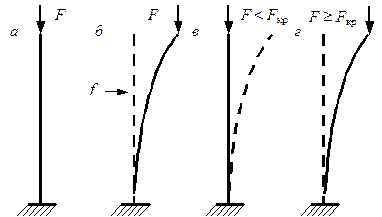 Рис. 6.1. Сжатый стержень:
а – до приложения возмущающей нагрузки;
б – под действием возмущающей нагрузки;
в – после снятия возмущающей нагрузки – прямолинейная форма равновесия устойчива;
г – после снятия возмущающей нагрузки – прямолинейная форма равновесия неустойчива
Рис. 6.1. Сжатый стержень:
а – до приложения возмущающей нагрузки;
б – под действием возмущающей нагрузки;
в – после снятия возмущающей нагрузки – прямолинейная форма равновесия устойчива;
г – после снятия возмущающей нагрузки – прямолинейная форма равновесия неустойчива
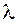 , которая ищется по формуле
, которая ищется по формуле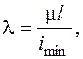 (6.1)
(6.1)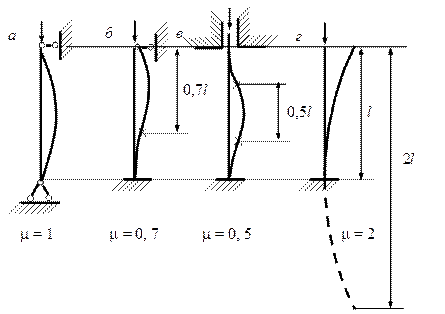 Рис. 6.2. Определение коэффициента m
для разных видов закрепления
Рис. 6.2. Определение коэффициента m
для разных видов закрепления
 – коэффициент, зависящий от условий закрепления стержня;
– коэффициент, зависящий от условий закрепления стержня; 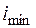 – минимальный радиус инерции поперечного сечения стержня. Рис. 6.2 демонстрирует, чему равен коэффициент
– минимальный радиус инерции поперечного сечения стержня. Рис. 6.2 демонстрирует, чему равен коэффициент 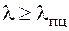 (стержень большой гибкости), то критическая сила определяется по формуле Эйлера
(стержень большой гибкости), то критическая сила определяется по формуле Эйлера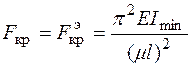 ; (6.2)
; (6.2) (стержень средней гибкости), то для нахождения критической силы используется формула Ясинского
(стержень средней гибкости), то для нахождения критической силы используется формула Ясинского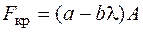 ; (6.3)
; (6.3)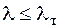 (стержень малой гибкости), то
(стержень малой гибкости), то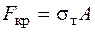 . (6.4)
. (6.4)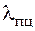 ,
,  , коэффициенты a и b в формуле Ясинского зависят от материала. Значение
, коэффициенты a и b в формуле Ясинского зависят от материала. Значение 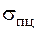 (материал должен подчиняться закону Гука). Из этого условия можно найти
(материал должен подчиняться закону Гука). Из этого условия можно найти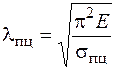 . (6.5)
. (6.5)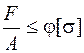 , (6.6)
, (6.6)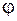 – коэффициент понижения допускаемых напряжений (или коэффициент продольного изгиба), зависящий от гибкости и материала стержня, – берется из таблиц. (Такая таблица приведена, например, в [2] на с. 370.)[15]
– коэффициент понижения допускаемых напряжений (или коэффициент продольного изгиба), зависящий от гибкости и материала стержня, – берется из таблиц. (Такая таблица приведена, например, в [2] на с. 370.)[15]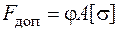 , (6.7)
, (6.7)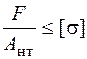 . (6.8)
. (6.8)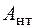 – так называемая площадь нетто, т. е. площадь сечения, равная полной площади
– так называемая площадь нетто, т. е. площадь сечения, равная полной площади 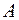 , уменьшенной на площадь
, уменьшенной на площадь 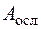 , занятую ослаблениями (отверстиями, выточками):
, занятую ослаблениями (отверстиями, выточками): 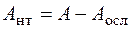 .
.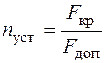 , (6.9)
, (6.9)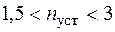 .
.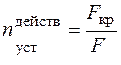 ,
,


