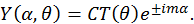В данном разделе на основе уравнения Шредингера описывается движение электрона в атоме, состоящем из положительно заряженного ядра — протона, обладающего массой  кг и положительным зарядом, равным по абсолютной величине заряду электрона
кг и положительным зарядом, равным по абсолютной величине заряду электрона  Кл. Реальным примером данной квантовой системы является атом водорода. Поскольку масса электрона
Кл. Реальным примером данной квантовой системы является атом водорода. Поскольку масса электрона
 кг на несколько порядков меньше массы протона, то движением последнего можно пренебречь и считать его покоящимся. Сила притяжения, действующая на электрон со стороны ядра, имеет электростатическую природу. Поэтому величина силы вычисляется из закона Кулона
кг на несколько порядков меньше массы протона, то движением последнего можно пренебречь и считать его покоящимся. Сила притяжения, действующая на электрон со стороны ядра, имеет электростатическую природу. Поэтому величина силы вычисляется из закона Кулона

где  — расстояние между частицами,
— расстояние между частицами,  Ф/м — диэлектрическая постоянная. При этом сила направлена по линии соединяющей частицы. Соответствующая последнему выражению потенциальная функция есть
Ф/м — диэлектрическая постоянная. При этом сила направлена по линии соединяющей частицы. Соответствующая последнему выражению потенциальная функция есть
 Рис. 8. Определение положения частицы
Рис. 8. Определение положения частицы  в сферической системе координат в сферической системе координат
|

Несмотря на то, что электрон совершает пространственное движения, сила, действующая на него со стороны ядра, зависит только от расстояния между частицами  . Поэтому, если принятое в нашем анализе неподвижным ядро поместить в начало координат, то потенциальная функция будет определяться только длиной радиуса вектора положения частицы
. Поэтому, если принятое в нашем анализе неподвижным ядро поместить в начало координат, то потенциальная функция будет определяться только длиной радиуса вектора положения частицы

где  — декартовы координаты положения электрона. Это обстоятельство делает целесообразным использовать не декартову, а сферическую систему координат, где положение частицы задается расстоянием от начала координат
— декартовы координаты положения электрона. Это обстоятельство делает целесообразным использовать не декартову, а сферическую систему координат, где положение частицы задается расстоянием от начала координат  и двумя углами — зенитным
и двумя углами — зенитным 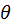 и азимутальным
и азимутальным  (рис. 8). Из рис. 8 нетрудно установить соотношения, связывающие декартовы и сферические координаты
(рис. 8). Из рис. 8 нетрудно установить соотношения, связывающие декартовы и сферические координаты


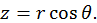
Входящий в стационарное уравнение Шредингера лапласиан волновой функции  имеет в сферической системе координат следующий вид:
имеет в сферической системе координат следующий вид:

Таким образом, стационарное уравнение Шредингера для электрона в поле положительного ядра будет иметь вид

где искомая волновая функция зависит от трех координат  .
.
Для решения последнего уравнения воспользуемся методом разделения переменных. Для чего представим искомую функцию в виде произведения двух функций, одна из которых зависит только от угловых координат, а вторая — только от радиальной: 
 . Подставив данное выражение в (22), умножив на
. Подставив данное выражение в (22), умножив на  и разделив на
и разделив на 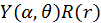 , получим
, получим

где  зависит только от
зависит только от  . В получившемся уравнении в левой части оставим функции, зависящие только от
. В получившемся уравнении в левой части оставим функции, зависящие только от  , а в правую часть вынесем выражения, содержащие только угловые координаты:
, а в правую часть вынесем выражения, содержащие только угловые координаты:

Левая часть полученного равенства содержит функции только независимой переменной  , а правая — только независимых переменных
, а правая — только независимых переменных  . Выполнение этого равенства при произвольных независимых изменениях указанных переменных будет возможно только в одном случае, когда обе его части равны одной и той же постоянной величине, которую обозначим
. Выполнение этого равенства при произвольных независимых изменениях указанных переменных будет возможно только в одном случае, когда обе его части равны одной и той же постоянной величине, которую обозначим 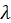 . Имеем
. Имеем


Таким образом, получаем два уравнения, связанные неизвестной пока постоянной 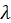 . Однако, неизвестные функции в этих уравнениях зависят от меньшего числа переменных. Первое уравнение
. Однако, неизвестные функции в этих уравнениях зависят от меньшего числа переменных. Первое уравнение

в качестве неизвестной функции содержит  , называемой радиальной составляющей волновой функции, второе
, называемой радиальной составляющей волновой функции, второе

содержит неизвестную функцию 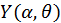 , называемую угловой составляющей волновой функции.
, называемую угловой составляющей волновой функции.
Обратимся к уравнению для угловой составляющей волновой функции (24). Представим функцию 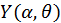 в виде произведения двух функций, каждая из которых зависит лишь от одной переменной
в виде произведения двух функций, каждая из которых зависит лишь от одной переменной  , и подставим в (24):
, и подставим в (24):

Разделив последнее уравнение на Φ Τ, умножив на  и разнося в разные части уравнения выражения, зависящие от
и разнося в разные части уравнения выражения, зависящие от  и
и 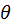 , получим
, получим

Как и ранее имеем равенство функций, зависящих от разных переменных, которые изменяются независимо друг от друга, что возможно лишь в случае если обе его части равны одной и той же постоянной величине, которую мы обозначим 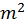 . В результате получим два обыкновенных дифференциальных уравнения
. В результате получим два обыкновенных дифференциальных уравнения


Общее решение второго из приведенных уравнений хорошо известно

где 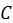 — постоянная. Требование однозначности решения при изменении азимутального угла на
— постоянная. Требование однозначности решения при изменении азимутального угла на  :
:  дает
дает

Следовательно, должно быть выполнено равенство  , что возможно только, если
, что возможно только, если  является целым числом, т. е.
является целым числом, т. е.
 .
.
Обратимся к уравнению (25) для функции  . В курсе математической физики показано, что решениями этого уравнения являются присоединенные функции Лежандра — семейство ортогональных полиномов относительно аргумента
. В курсе математической физики показано, что решениями этого уравнения являются присоединенные функции Лежандра — семейство ортогональных полиномов относительно аргумента  . При этом решение уравнения (25) существует лишь для дискретного набора значений параметра уравнения (25)
. При этом решение уравнения (25) существует лишь для дискретного набора значений параметра уравнения (25) 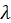 , вычисляемых по соотношению
, вычисляемых по соотношению  , где
, где 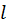 — целые числа, причем
— целые числа, причем  .
.
Можно показать (см. любой общий курс квантовой механики), что оператор квадрата момента импульса частицы[1] есть

Действуя этим оператором на угловую составляющую волновой функции, получим
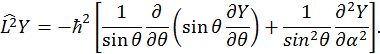
Причем нетрудно видеть, что выражение в квадратных скобках представляет собой сумму двух первых слагаемых в уравнении (24), которую легко выразить через третье. Поэтому получаем

Следовательно,  являются собственными числами оператора квадрата момента импульса. Как было показано выше, собственные числа оператора физической величины совпадают со значениями этой физической величины. Поэтому квадрат момента импульса электрона с учетом равенства
являются собственными числами оператора квадрата момента импульса. Как было показано выше, собственные числа оператора физической величины совпадают со значениями этой физической величины. Поэтому квадрат момента импульса электрона с учетом равенства  , будет принимать значения
, будет принимать значения  , а модуль момента импульса будет равен
, а модуль момента импульса будет равен

Из последней формулы видно, что число целое l однозначно определяет модуль момента импульса частицы. Поэтому число 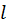 называется орбитальным квантовым числом.
называется орбитальным квантовым числом.
Проекция момента импульса на ось  в классической механике в соответствии с общим определением вычисляется по формуле
в классической механике в соответствии с общим определением вычисляется по формуле
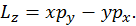
Вспоминая данное в разделе 1.2 определение оператора импульса в квантовой механике, нетрудно составить выражение для оператора  -проекции момента импульса
-проекции момента импульса

Используя приведенные выше соотношения, связывающие декартовы и сферические координаты, можно показать, что

Действуя оператором  на функцию
на функцию  , получим
, получим

Подставляя в последнюю формулу найденное выше выражение для  , приходим к равенству
, приходим к равенству

Откуда видно, что числа  являются собственными числами оператора проекции момента импульса на ось
являются собственными числами оператора проекции момента импульса на ось  . Следовательно, упомянутая проекция принимает значения, определяемые формулой
. Следовательно, упомянутая проекция принимает значения, определяемые формулой
 ,
, 
В отличие от орбитального квантового числа 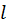 число
число  задает не только величину, но и знак проекции момента импульса, который в интерпретации классической механики определяет направление вращения частицы вокруг центра. В случае заряженной частицы направление вращения определяет знак возникающего при этом магнитного поля. Поэтому число
задает не только величину, но и знак проекции момента импульса, который в интерпретации классической механики определяет направление вращения частицы вокруг центра. В случае заряженной частицы направление вращения определяет знак возникающего при этом магнитного поля. Поэтому число  носит название магнитного квантового числа.
носит название магнитного квантового числа.
Решения, приведенные в табл. 1, представляют собой произведение константы на функцию  , являющуюся решением уравнения (25), и на найденную функцию
, являющуюся решением уравнения (25), и на найденную функцию  :
: 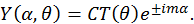
Таблица 1


 кг и положительным зарядом, равным по абсолютной величине заряду электрона
кг и положительным зарядом, равным по абсолютной величине заряду электрона  Кл. Реальным примером данной квантовой системы является атом водорода. Поскольку масса электрона
Кл. Реальным примером данной квантовой системы является атом водорода. Поскольку масса электрона  кг на несколько порядков меньше массы протона, то движением последнего можно пренебречь и считать его покоящимся. Сила притяжения, действующая на электрон со стороны ядра, имеет электростатическую природу. Поэтому величина силы вычисляется из закона Кулона
кг на несколько порядков меньше массы протона, то движением последнего можно пренебречь и считать его покоящимся. Сила притяжения, действующая на электрон со стороны ядра, имеет электростатическую природу. Поэтому величина силы вычисляется из закона Кулона
 — расстояние между частицами,
— расстояние между частицами,  Ф/м — диэлектрическая постоянная. При этом сила направлена по линии соединяющей частицы. Соответствующая последнему выражению потенциальная функция есть
Ф/м — диэлектрическая постоянная. При этом сила направлена по линии соединяющей частицы. Соответствующая последнему выражению потенциальная функция есть Рис. 8. Определение положения частицы
Рис. 8. Определение положения частицы  в сферической системе координат
в сферической системе координат

 — декартовы координаты положения электрона. Это обстоятельство делает целесообразным использовать не декартову, а сферическую систему координат, где положение частицы задается расстоянием от начала координат
— декартовы координаты положения электрона. Это обстоятельство делает целесообразным использовать не декартову, а сферическую систему координат, где положение частицы задается расстоянием от начала координат 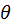 и азимутальным
и азимутальным  (рис. 8). Из рис. 8 нетрудно установить соотношения, связывающие декартовы и сферические координаты
(рис. 8). Из рис. 8 нетрудно установить соотношения, связывающие декартовы и сферические координаты

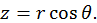
 имеет в сферической системе координат следующий вид:
имеет в сферической системе координат следующий вид:

 .
.
 . Подставив данное выражение в (22), умножив на
. Подставив данное выражение в (22), умножив на  и разделив на
и разделив на 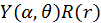 , получим
, получим
 зависит только от
зависит только от 
 . Выполнение этого равенства при произвольных независимых изменениях указанных переменных будет возможно только в одном случае, когда обе его части равны одной и той же постоянной величине, которую обозначим
. Выполнение этого равенства при произвольных независимых изменениях указанных переменных будет возможно только в одном случае, когда обе его части равны одной и той же постоянной величине, которую обозначим 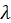 . Имеем
. Имеем


 , называемой радиальной составляющей волновой функции, второе
, называемой радиальной составляющей волновой функции, второе
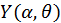 , называемую угловой составляющей волновой функции.
, называемую угловой составляющей волновой функции. , и подставим в (24):
, и подставим в (24):
 и разнося в разные части уравнения выражения, зависящие от
и разнося в разные части уравнения выражения, зависящие от 
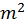 . В результате получим два обыкновенных дифференциальных уравнения
. В результате получим два обыкновенных дифференциальных уравнения


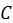 — постоянная. Требование однозначности решения при изменении азимутального угла на
— постоянная. Требование однозначности решения при изменении азимутального угла на  :
:  дает
дает
 , что возможно только, если
, что возможно только, если  является целым числом, т. е.
является целым числом, т. е.  .
. . В курсе математической физики показано, что решениями этого уравнения являются присоединенные функции Лежандра — семейство ортогональных полиномов относительно аргумента
. В курсе математической физики показано, что решениями этого уравнения являются присоединенные функции Лежандра — семейство ортогональных полиномов относительно аргумента  . При этом решение уравнения (25) существует лишь для дискретного набора значений параметра уравнения (25)
. При этом решение уравнения (25) существует лишь для дискретного набора значений параметра уравнения (25)  , где
, где 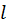 — целые числа, причем
— целые числа, причем  .
.
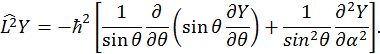

 являются собственными числами оператора квадрата момента импульса. Как было показано выше, собственные числа оператора физической величины совпадают со значениями этой физической величины. Поэтому квадрат момента импульса электрона с учетом равенства
являются собственными числами оператора квадрата момента импульса. Как было показано выше, собственные числа оператора физической величины совпадают со значениями этой физической величины. Поэтому квадрат момента импульса электрона с учетом равенства  , а модуль момента импульса будет равен
, а модуль момента импульса будет равен
 в классической механике в соответствии с общим определением вычисляется по формуле
в классической механике в соответствии с общим определением вычисляется по формуле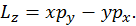


 на функцию
на функцию  , получим
, получим
 , приходим к равенству
, приходим к равенству
 являются собственными числами оператора проекции момента импульса на ось
являются собственными числами оператора проекции момента импульса на ось  ,
,