Пусть в области  плоскости (
плоскости ( ) задана однозначная непрерывная функция
) задана однозначная непрерывная функция  и пусть
и пусть  – кусочно-гладкая направленная кривая, принадлежащая
– кусочно-гладкая направленная кривая, принадлежащая  вместе со своими концами
вместе со своими концами  и
и  .
.
По определению полагают
 , (1)
, (1)
где  – произвольная точка элементарной дуги
– произвольная точка элементарной дуги 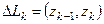 при произвольном разбиении дуги
при произвольном разбиении дуги  на
на 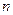 частей точками
частей точками  .
.
При данных условиях интеграл от функции  вдоль кривой
вдоль кривой  , как предел интегральной суммы (1), существует.
, как предел интегральной суммы (1), существует.
Пример 1. Пользуясь определением (1), вычислим  , где
, где  – радиус-вектор точки
– радиус-вектор точки  .
.
Разобьем радиус-вектор точки  на п равных частей, т.е. полагаем
на п равных частей, т.е. полагаем
 .
.
Пусть  , тогда интегральная сумма запишется в виде
, тогда интегральная сумма запишется в виде
 .
.
Следовательно,
 .●
.●
Вычисление интеграла от функции комплексного переменного сводится к вычислению двух криволинейных интегралов 2-го рода по формуле
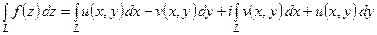 . (2)
. (2)
Из формулы (2) следует, что на интегралы от функции комплексного переменного распространяются известные свойства криволинейных интегралов.
Пример 2. Вычислим интеграл  , где
, где  – верхняя полуокружность
– верхняя полуокружность  с обходом против часовой стрелки.
с обходом против часовой стрелки.
Имеем
 .
.
Переходя к параметрическому уравнению кривой 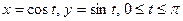 , и учитывая, что
, и учитывая, что  в точках кривой, получаем
в точках кривой, получаем
 .●
.●
Если кривая задана параметрическими уравнениями  , что равносильно одному уравнению в комплексной форме
, что равносильно одному уравнению в комплексной форме 
 , то имеет место удобная для вычисления интеграла формула
, то имеет место удобная для вычисления интеграла формула
 (3)
(3)
Интеграл  , вообще говоря, зависит от пути интегрирования. Условием независимости интеграла от пути интегрирования является аналитичность подынтегральной функции.
, вообще говоря, зависит от пути интегрирования. Условием независимости интеграла от пути интегрирования является аналитичность подынтегральной функции.
Важную роль в теории функций комплексного переменного играет интегральная теорема Коши. Приведем две формулировки теоремы: для одно- и многосвязной областей.
Пусть  – кусочно-гладкая замкнутая кривая, будем ее называть замкнутым контуром.
– кусочно-гладкая замкнутая кривая, будем ее называть замкнутым контуром.
Теорема Коши(для односвязной области). Пусть функция  аналитична в односвязной области
аналитична в односвязной области  , тогда для любого замкнутого контура
, тогда для любого замкнутого контура  имеет место равенство
имеет место равенство
 . (4)
. (4)

Теорема Коши(для многосвязной области). Пусть  аналитична в многосвязной области
аналитична в многосвязной области  , ограниченной внешним контуром
, ограниченной внешним контуром  и внутренними контурами
и внутренними контурами  . Тогда имеет место равенство
. Тогда имеет место равенство

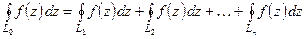 (5)
(5)
при условии, что интегрирование по всем контурам производится против часовой стрелки.

Как следствие последней теоремы (для двусвязной области) следует отметить утверждение: если  аналитична в области
аналитична в области  всюду, кроме
всюду, кроме  , то
, то
 , (6)
, (6)
где  и
и  – произвольные контуры в
– произвольные контуры в  , содержащие особую точку
, содержащие особую точку  .
.

Для аналитической функции имеет место формула Ньютона-Лейбница
 , (7)
, (7)
где  – первообразная для
– первообразная для  , т.е.
, т.е.  . Этой формулой можно пользоваться для вычисления интеграла вдоль пути, лежащего в односвязной области, где
. Этой формулой можно пользоваться для вычисления интеграла вдоль пути, лежащего в односвязной области, где  аналитична, если известна первообразная для
аналитична, если известна первообразная для  .
.
Техника нахождения неопределенных интегралов в комплексном анализе та же, что и в действительном, таблица основных интегралов в обоих случаях одинакова
Если  аналитична в области
аналитична в области  ,
,  и
и  контур, охватывающий точку
контур, охватывающий точку  , то справедлива интегральная формула Коши
, то справедлива интегральная формула Коши
 . (8)
. (8)
При этом функция  имеет всюду в
имеет всюду в  производные любого порядка, для которых справедливы формулы
производные любого порядка, для которых справедливы формулы
 (9)
(9)
(контур  может быть объединением контуров
может быть объединением контуров 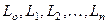 ).
).
Интеграл в правой части формулы (1) называется интегралом Коши.
Интегральная формула Коши позволяет находить значение аналитической функции в любой точке, лежащей внутри области  , если известны значения этой функции на контуре
, если известны значения этой функции на контуре  , ограничивающем
, ограничивающем  . Если точка
. Если точка  лежит вне области
лежит вне области  , то интеграл Коши равен нулю в силу теоремы Коши, так как в этом случае подынтегральная функция является аналитической в области
, то интеграл Коши равен нулю в силу теоремы Коши, так как в этом случае подынтегральная функция является аналитической в области  .
.
Формулы (1) и (2) могут служить для вычисления интегралов по замкнутым контурам.
Пример 3. Вычислим интеграл

Запишем интеграл в виде  и, используя формулу Коши (8), находим
и, используя формулу Коши (8), находим

 .●
.●

 плоскости (
плоскости ( ) задана однозначная непрерывная функция
) задана однозначная непрерывная функция  и пусть
и пусть  – кусочно-гладкая направленная кривая, принадлежащая
– кусочно-гладкая направленная кривая, принадлежащая  и
и  .
. , (1)
, (1) – произвольная точка элементарной дуги
– произвольная точка элементарной дуги 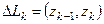 при произвольном разбиении дуги
при произвольном разбиении дуги 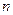 частей точками
частей точками  .
. вдоль кривой
вдоль кривой  , где
, где  .
. .
. , тогда интегральная сумма запишется в виде
, тогда интегральная сумма запишется в виде .
. .●
.●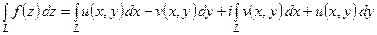 . (2)
. (2) , где
, где  с обходом против часовой стрелки.
с обходом против часовой стрелки. .
.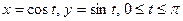 , и учитывая, что
, и учитывая, что  в точках кривой, получаем
в точках кривой, получаем .●
.● , что равносильно одному уравнению в комплексной форме
, что равносильно одному уравнению в комплексной форме 
 , то имеет место удобная для вычисления интеграла формула
, то имеет место удобная для вычисления интеграла формула (3)
(3) , вообще говоря, зависит от пути интегрирования. Условием независимости интеграла от пути интегрирования является аналитичность подынтегральной функции.
, вообще говоря, зависит от пути интегрирования. Условием независимости интеграла от пути интегрирования является аналитичность подынтегральной функции. имеет место равенство
имеет место равенство . (4)
. (4)
 и внутренними контурами
и внутренними контурами  . Тогда имеет место равенство
. Тогда имеет место равенство
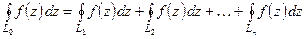 (5)
(5)
 , то
, то , (6)
, (6) и
и  – произвольные контуры в
– произвольные контуры в  , содержащие особую точку
, содержащие особую точку 
 , (7)
, (7) – первообразная для
– первообразная для  . Этой формулой можно пользоваться для вычисления интеграла вдоль пути, лежащего в односвязной области, где
. Этой формулой можно пользоваться для вычисления интеграла вдоль пути, лежащего в односвязной области, где  аналитична, если известна первообразная для
аналитична, если известна первообразная для  контур, охватывающий точку
контур, охватывающий точку  . (8)
. (8) (9)
(9)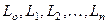 ).
).
 и, используя формулу Коши (8), находим
и, используя формулу Коши (8), находим
 .●
.●


