В этой точке выполнялись условия
называемые условиями Коши-Римана (С-R) или Даламбера-Эйлера. При выполнении условий (C-R) производная функции может быть найдена по одной из следующих формул:
Приведем два определения, имеющих фундаментальное значение в теории функции комплексного переменного. Определение. Однозначная функция называется аналитической в точке Определение. Функция называется аналитической в области, если она дифференцируема в каждой точке этой области. Аналитичность функции в точке и дифференцируемость в точке – разные понятия. Если функция аналитична в точке, то она, безусловно, дифференцируема в ней, но обратное может и не иметь места. Функция может быть дифференцируема в точке, но не быть дифференцируемой ни в какой окрестности этой точки, в таком случае она не будет аналитической в рассматриваемой точке. Условием аналитичности функции в области является выполнимость условий Коши-Римана для всех точек этой области. Пример. Выясним, является ли аналитичнойфункция Так как
Проверим выполнение условий (C-R):
. Условия (C-R) выполняются при любых конечных х и у, значит функция аналитична во всей комплексной плоскости (кроме Определение. Точки, в которых Геометрический смысл модуля и аргумента производной. Пусть функция Модуль производной
Для аргумента производной можно записать
где Пусть Таким образом, геометрический смысл модуля и аргумента производной состоит в том, что при отображении, осуществляемом аналитической функцией, удовлетворяющей условию Если рассмотреть две кривые Определение. Отображение области Отображение, осуществляемое аналитической функцией, является конформным во всех точках, в которых Например, функция
|

 ,(2)
,(2) (3)
(3) , если она дифференцируема в некоторой окрестности точки
, если она дифференцируема в некоторой окрестности точки  .
. ,имеем
,имеем  . Отсюда
. Отсюда ,
,  .
.
 ,
, ).●
).● является аналитической, называются регулярными (правильными). Если
является аналитической, называются регулярными (правильными). Если  , за исключением некоторых точек, то эти точки называются особыми. Точка
, за исключением некоторых точек, то эти точки называются особыми. Точка  называется изолированной особой точкой, если вокруг нее можно описать круг, не содержащий других особых точек.
называется изолированной особой точкой, если вокруг нее можно описать круг, не содержащий других особых точек. дифференцируема в области
дифференцируема в области  . Функция отобразит точку
. Функция отобразит точку  в точку
в точку  плоскости
плоскости  , кривую
, кривую  , проходящую через точку
, проходящую через точку  , проходящую через
, проходящую через 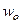 .
. есть предел отношения бесконечно малого расстояния между отображенными точками
есть предел отношения бесконечно малого расстояния между отображенными точками  к бесконечно малому расстоянию между их прообразами
к бесконечно малому расстоянию между их прообразами  . Поэтому величину
. Поэтому величину  можно рассматривать геометрически как коэффициент растяжения (если
можно рассматривать геометрически как коэффициент растяжения (если  ) в точке
) в точке  при отображении области
при отображении области  в области
в области  , осуществляемом функцией
, осуществляемом функцией  будет свой.
будет свой.

 ,
, и
и  это углы
это углы 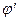 и
и  , которые векторы
, которые векторы  и
и  образуют с действительной осью.
образуют с действительной осью. и
и  углы, образованные касательными к кривой
углы, образованные касательными к кривой 
 , а
, а  , поэтому
, поэтому  определяет угол, на который нужно повернуть касательную к кривой
определяет угол, на который нужно повернуть касательную к кривой  , модуль k определяет коэффициент преобразования подобия бесконечно малого линейного элемента в точке
, модуль k определяет коэффициент преобразования подобия бесконечно малого линейного элемента в точке  и
и  ,
,  и
и  , то углы
, то углы  и
и  между их касательными, вообще говоря, неравные.
между их касательными, вообще говоря, неравные. на область
на область  , обладающее свойствами постоянства растяжений (
, обладающее свойствами постоянства растяжений ( ) в любом направлении и сохранения (или консерватизма) углов
) в любом направлении и сохранения (или консерватизма) углов  между двумя кривыми, пересекающимися в точке
между двумя кривыми, пересекающимися в точке  .
.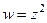 задает отображение, которое является конформным во всех точках, кроме точки (0; 0).
задает отображение, которое является конформным во всех точках, кроме точки (0; 0).


