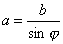ОБЩЕЕ УРАВНЕНИЕ КРИВОЙ КРИВАЯ ВТОРОГО ПОРЯДКА
Общее уравнение второго порядка с двумя переменными имеет вид А х 2 + В ху + С у 2 + D x + Е у + F = 0, A2 + В2 + С2 =/= 0. (2) Возникает естественный вопрос, что представляет собой множество точек плоскости, координаты которых удовлетворяют уравнению (2)? Другими словами, какие множества точек плоскости могут задаваться этим уравнением? Покажем, что существует 8 различных типов таких множеств. 1) Положив в уравнении (2) А = 1/ a 2, С = 1/ b 2, F = — l, B = D = E = 0, получим
Итак, уравнение (2) может быть уравнением эллипса. 2) Положив в уравнении (2) А = 1/ a 2, С = — 1/ b 2, F = — l, B = D = E = 0, получим
Следовательно, уравнение (2) может быть уравнением гиперболы. 3) Если в уравнении (2) положить C = l, D = — 2 p, A = В = E = F = 0, то получим у 2 = 2 рх. Уравнение (2) может быть уравнением параболы. 4) Если в уравнении (2) выбрать коэффициенты следующим образом: А = а 2, C = — b 2, B = D = E = F = 0, то оно примет вид а 2 х 2 — b 2 у 2 = 0. Так как а 2 х 2 — b 2 у 2 = (ах — by) (ах + by), то это уравнение является уравнением двух прямых: ах — by = 0 и ах + by = 0. Таким образом, уравнением (2) может задаваться пара пересекающихся прямых. 5) Взяв в уравнении (2) C = l, F = — а 2, A = B = D = E = 0, получим у 2 — а 2 = 0, т. е. уравнение двух прямых у = а и у = —а. Следовательно, уравнение (2) может быть уравнением двух параллельных прямых. 6) Положив в уравнении (2) С = 1, A = B = D = E = F = 0, получим у 2 = 0. Такое уравнение принято считать уравнением пары совпавших прямых, так как из него следует, что у • у = 0 и, приравнивая каждый множитель нулю, получаем у = 0 и у = 0. Итак, уравнением (2) может быть задача пара совпавших прямых. 7) Если в уравнении (2) возьмем А = а 2, С = b 2, B = D = E = F = 0, то получим а 2 х 2 + b 2 у 2 = 0. Этому уравнению удовлетворяют координаты только одной точки плоскости, а именно точки (0; 0). Отсюда следует, что уравнение (2) может задавать точку. 8) Положив в уравнении (2) А = 1/ a 2, С = 1/ b 2, F = l, B = D = E = 0, получим
Этому уравнению не удовлетворяют координаты ни одной точки плоскости. То же получится и в случае, когда C = l, F = а 2 =/= 0, A = B = D = E = 0. На плоскости нет точек, координаты которых удовлетворяют уравнению y 2 + а 2 = 0. Таким образом, уравнение (2) может быть уравнением пустого множества. Мы показали, что уравнение (2) может быть уравнением 1) эллипса, 2) гиперболы, 3) параболы, 4) пары пересекающихся прямых, 5) пары параллельных прямых, 6) пары совпавших прямых, 7) точки, 8) пустого множества. ЭЛИПС Эллипсом называется геометрическое место точек, для которых сумма расстояний до двух фиксированных точек плоскости, называемых фокусами, есть постоянная величина, большая, чем расстояние между фокусами. Постоянную сумму расстояний произвольной точки эллипса до фокусов принято обозначать через 2а. Фокусы эллипса обозначают буквами Пусть дан эллипс. Если оси декартовой прямоугольной системы координат выбраны так, что фокусы данного эллипса располагаются на оси абсцисс симметрично относительно начала координат, то в этой системе координат уравнение данного эллипса имеет вид
где
При указанном выборе системы координат оси координат являются осями симметрии эллипса, а начало координат - его центром симметрии (рис.). Оси симметрии эллипса называются просто его осями, центр симметрии - просто центром. Точки, в которых эллипс пересекает свои оси, называются его вершинами. На рис. Вершины эллипса суть точки A’, A, B’, B. Часто осями эллипса называются также отрезки A’A=2a и B’B=2b; вместе с тем отрезок ОА=а называют большой полуосью эллипса, отрезок OB=b - малой полуосью. Если фокусы эллипса расположены на оси Оу (симметрично относительно начала координат), то уравнение эллипса имеет тот же вид (1), но в этом случае Число
где а - большая полуось, называется эксцентриситетом эллипса. Очевидно,
Если эллипс определен уравнением (1) и
(рис.) называются директрисами эллипса (если Каждая директриса обладает следующим свойством: если r - расстояние от произвольной точки эллипса до некоторого фокуса, d - расстояние от той же точки до односторонней с этим фокусом директрисы, то отношение r/d есть постоянная величина, равная эксцентриситету эллипса:
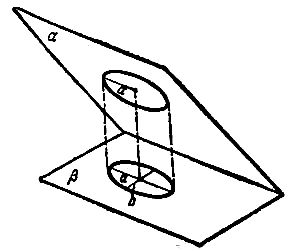
Если две плоскости
(рис.).
Если круглый цилиндр имеет в качестве направляющей окружность радиуса b, то в сечении этого цилиндра плоскостью, наклоненной к оси цилиндра под острым углом
(рис.).
|

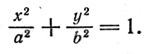
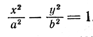
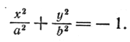
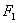 и
и 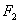 , расстояние между ними - через 2с. По определению эллипса
, расстояние между ними - через 2с. По определению эллипса 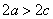 или
или  .
.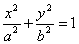 (1)
(1)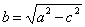 ; очевидно,
; очевидно, 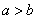 . Уравнение вида (1) называется каноническим уравнением эллипса.
. Уравнение вида (1) называется каноническим уравнением эллипса.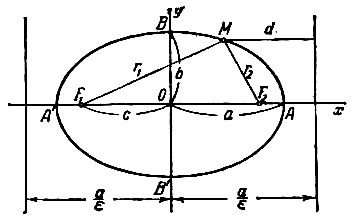
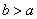 ; следовательно, если мы желаем буквой а обозначать большую полуось, то в уравнении (1) нужно буквы а и b поменять местами. Однако для удобства формулировок задач мы условимся буквой а всегда обозначать полуось, расположенную на оси Ох, буквой b - полуось, расположенную на оси Оу, независимо от того, что больше, a или b. Если a=b, то уравнение (1) определяет окружность, рассматриваемую как частный случай эллипса.
; следовательно, если мы желаем буквой а обозначать большую полуось, то в уравнении (1) нужно буквы а и b поменять местами. Однако для удобства формулировок задач мы условимся буквой а всегда обозначать полуось, расположенную на оси Ох, буквой b - полуось, расположенную на оси Оу, независимо от того, что больше, a или b. Если a=b, то уравнение (1) определяет окружность, рассматриваемую как частный случай эллипса.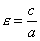
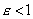 (для окружности
(для окружности 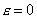 ). Если М(x; y) - произвольная точка эллипса, то отрезки
). Если М(x; y) - произвольная точка эллипса, то отрезки  и
и 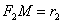 (рис.) называются фокальными радиусами точки М. Фокальные радиусы могут быть вычислены по формулам
(рис.) называются фокальными радиусами точки М. Фокальные радиусы могут быть вычислены по формулам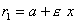 ,
, 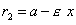 .
. ,
, 
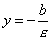 ,
, 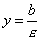 .
.
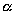 и
и 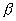 образуют острый угол
образуют острый угол  , то проекциейй на плоскость
, то проекциейй на плоскость