Свойства степенных функций и их графики· Степенная функция с показателем равным нулю, p = 0 Если показатель степенной функции y = x p равен нулю, p = 0, то степенная функция определена для всех x ≠ 0 и является постоянной, равной единице: · Степенная функция с натуральным нечетным показателем, p = n = 1, 3, 5,... Рассмотрим степенную функцию y = x p = x n с натуральным нечетным показателем степени n = 1, 3, 5,.... Такой показатель также можно записать в виде: n = 2k + 1, где k = 0, 1, 2, 3,... – целое не отрицательное. Ниже представлены свойства и графики таких функций.
График степенной функции y = x n с натуральным нечетным показателем при различных значениях показателя степени n = 1, 3, 5,.... Область определения: –∞ < x < ∞;
· Степенная функция с натуральным четным показателем, p = n = 2, 4, 6,... Рассмотрим степенную функцию y = x p = x n с натуральным четным показателем степени n = 2, 4, 6,.... Такой показатель также можно записать в виде: n = 2k, где k = 1, 2, 3,... – натуральное. Свойства и графики таких функций даны ниже.
График степенной функции y = x n с натуральным четным показателем при различных значениях показателя степениn = 2, 4, 6,.... Область определения: –∞ < x < ∞;
· Степенная функция с целым отрицательным показателем, p = n = -1, -2, -3,... Рассмотрим степенную функцию y = x p = x n с целым отрицательным показателем степени n = -1, -2, -3,.... Если положить n = –k, где k = 1, 2, 3,... – натуральное, то ее можно представить в виде:
График степенной функции y = x n с целым отрицательным показателем при различных значениях показателя степени n = -1, -2, -3,.... Нечетный показатель, n = -1, -3, -5,... Ниже представлены свойства функции y = x n с нечетным отрицательным показателем n = -1, -3, -5,.... Область определения: x ≠ 0
Четный показатель, n = -2, -4, -6,... Ниже представлены свойства функции y = x n с четным отрицательным Область определения: x ≠ 0 Билет№7 Логарифмическая функция
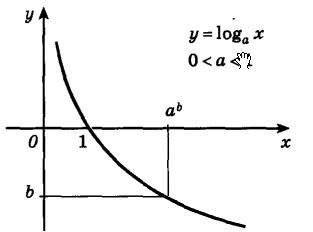
Функцию вида y = loga(x), где a любое положительное число не равное единице, называют логарифмической функцией с основанием а.
Основные свойства логарифмической функции: 1. Областью определения логарифмической функции будет являться множество положительных вещественных чисел. 2. Областью значения логарифмической функции будет являться множество вещественных чисел. 3. Если основание логарифмической функции a>1, то на всей области определения функции возрастает 4. График логарифмической функции всегда проходит через точку (1;0). 5. Возрастающая логарифмическая функция, будет положительной при x>1, и отрицательной при 0<х<1. 6. Убывающая логарифмическая функция, будет отрицательной при х>1, и положительной при 0<x<1:
На следующем рисунке представлен график убывающей логарифмической функции - (0<a<1):
7. Функция не является четной или нечетной. Логарифмическая функция – функция общего вида. 8. Функция не имеет точек максимума и минимума. Билет №8: Показательная функция (свойства, график). Показательная функция - функция вида ü Графики функций:
ü Свойства функции 1) Обл. опред. = ( 2) Обл. знач. = ( 3) Не обладает св-ми четности, нечетности 4) Функц. является возрастающей на R, если а Функц. является убывающей на R, если 0 5) У=0 (Ох) - является асимптотой графика 6) Функц. Не имеет наиб.\наим. Значений 7) Функция ограничена снизу Билет №9: Тригонометрические функции ( 1) Х
Определение: Функция у=f(x) называется периодической с периодом Т. Т
ü Свойства: 1) Обл.опред. - х 2) у 3) нечетная 4) периодическая, Т=2 5) возрастает убывает 6) у у у=0, если х= 7) ограничена снизу и сверху 8) непрерывна
Ø у=
ü Свойства: 1) х 2) у= 3) четная 4) периодическая Т=2π - наим.положит. период 5) возрастает убывает 6) у у у=0, х 7) ограничена сверху и снизу 8) непрерывна
Ø у= tg x
tg=(-x)=-tgx
ü Свойства: 1) Х 2) Нечетная 3) Т= π 4) Возрастает (- 5) У у у=0, х= πr 6) не ограничена ни сверху, ни снизу 7) непрерывна на промежутках вида (-
Билет №10: Определение логарифма. Свойства логарифмов (логарифм произведения, частного, степени, формула перехода с выводом). Логарифмом положительного числа ЕСЛИ ЧТО, Х – ЭТО УМНОЖИТЬ ü Свойства логарифмов:
· Вывод:
Перемножим эти 2 равенства:
· Вывод::
Разделим первое равенство на второе:
· ·
·
Билет №11: Десятичные и натуральные логарифмы. Натуральный логарифм — это логарифм по основанию е, где e — иррациональная константа, равная приблизительно 2,7. Натуральный логарифм обычно обозначают как ln(x), log e (x) или иногда просто log(x), если основание e подразумевается. Десятичный логарифм — логарифм по основанию 10. Другими словами, десятичный логарифм числа b есть решение уравнения Десятичный логарифм числа b существует, если b
Билет №12: Определение sin, cos, tg, ctg угла. Косинус острого угла в прямоугольном треугольнике — это отношение прилежащего катета к гипотенузе: Синус острого угла в прямоугольном треугольнике — это отношение противолежащего катета к гипотенузе: Тангенс острого угла в прямоугольном треугольнике — это отношение противолежащего катета к прилежащему: Котангенс острого угла в прямоугольном треугольнике — это отношение прилежащего катета к противолежащему: Билет №13: Зависимость между sin, cos, tg, ctg одного и того же угла. · · · 1+ · 1+
Билет№14: Формулы сложения. · cos(х +у) = cosу · cos(х - у) = cosу · sin(х + у) = sinх · sin(х - у) = sinх · ·
Билет №15 «Формулы двойного угла c выводом» 1) Для синуса: Sin(x+y)=sinx·cosy+cosx·siny
2) Для косинуса: Cos(x+y)=cosx·cosy-sinx·siny
3) Для тангенса: Tg(x+y)= Tg(x+x)=
Билет №16 «Формулы приведения с выводом» 1) Если под знаком преобразуемой тригонометрической функции содержитя выражение π+t, π-t, 2π+t или 2π-t, то наименование тригонометрической функции следует сохранить. 2) Если под знаком преобразуемой тригонометрической функции содержится выражение 3) Перед полученной функцией от аргумента t надо поставить тот знак, который имела бы преобразуемая функция при условии, что 0<t<
Примеры: Sin( Cos( Sin cos tg( ctg(
Билет №17 «Сумма и разность sin (cos) с выводом» 1) Sint + sins = 2sin Sin(x+y)=sinx·cosy+cosx·siny + Sin(x-y)= sinx·cosy-cosx·siny Sin(x+y) + Sin(x-y)=2sinxcosy Пусть х+у=t, x-y=S à x= 2) sint – sins=2sin Sin(x+y)=sinx·cosy+cosx·siny - Sin(x-y)= sinx·cosy-cosx·siny Sin(x+y)-Sin(x-y)=2cosx·siny Пусть х+у=t, x-y=S à x= 3) cost + cosS = 2cos Cos(x+y)=cosу + Cos(x-y)= cosу Cos(x+y)+cos(x-y)=2cosycosx Пусть х+у=t, x-y=S à x= 4) cost - cosS = 2sin Cos(x+y)=cosу - Cos(x-y)= cosу Cos(x+y)-cos(x-y)= -2sinysinx Пусть х+у=t, x-y=S à x= Билет №18 «Радианная и градусная мера угла» Угол в 1˚ - это центральный угол, опирающийся на дугу, составляющую
Угол в 1 радиан – это центральный угол, опирающийся в единичной окружности на дугу длиной 1, а в окружности произвольного размера – на дугу, длина которой равна радиусу окружности.
1˚=
1 рад =
Примеры: 1) 35˚ = 2) Билет № 19 «Решение уравнений cos, sin, tg (arccos, arcsin, arctg числа)» Уравнение cos x = a. Принцип:
Формулы:
Уравнение sin x = a. Принцип:
|






 , a
, a 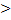 0, а
0, а  0.
0.





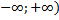



 )
)
 R, у=
R, у= 
 - нечетность функции
- нечетность функции ) =
) = 
 , если для любого х выполняется равенство: f(x - T)=f(x)=f(x+T)
, если для любого х выполняется равенство: f(x - T)=f(x)=f(x+T) Синусоида:
Синусоида:



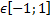
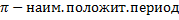


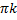 ;
;  )
)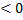 , если х
, если х 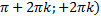

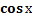

 Косинусоида:
Косинусоида:

 +2πk;
+2πk;  +2πk)
+2πk)
 πk, k
πk, k 




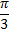


 +πk,
+πk, 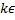 z
z
 х
х  πk)
πk) b по основанию а, называется показатель степени, в которую нужно возвести а, чтобы получить b.
b по основанию а, называется показатель степени, в которую нужно возвести а, чтобы получить b.  =x
=x 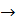
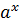 = b, при а
= b, при а 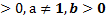
 Логарифм произведения:
Логарифм произведения: , b
, b 
 = b
= b = c
= c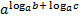 = b Х с
= b Х с +
+  =
= 
 =
= 
 = b:c
= b:c
 = m
= m 
 =
= 

 =b
=b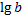 . Примеры:
. Примеры: ;
; 



 =
= 
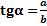

 +
+  1
1 =1
=1 =
= 
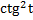 =
= 
 cosх
cosх 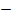 sinх
sinх  sinу
sinу

 x-
x- 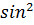 x
x

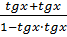

 ,
,  ,
,  или
или  , то наименование тригонометрической функции следует изменить на родственное (синус – на косинус, косинус – на синус, тангенс – на котангенс, котангенс – на тангенс).
, то наименование тригонометрической функции следует изменить на родственное (синус – на косинус, косинус – на синус, тангенс – на котангенс, котангенс – на тангенс).
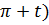 =-sint
=-sint =cost
=cost cos
cos 
 , y=
, y=  cosх
cosх  sinх
sinх 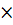 sinу
sinу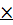 cosx + sinх
cosx + sinх 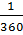 части окружности.
части окружности. рад
рад
 ·35 =
·35 =  рад
рад рад =
рад = 


