Показатели вариацииК показателям вариации относятся: размах вариации, среднее линейное отклонение, дисперсия, среднее квадратическое отклонение, коэффициент вариации. Самым элементарным показателем вариации признака является размах
Однако размах вариации показывает лишь крайние отклонения признака и не отражает отклонений всех вариантов в ряду. При изучении вариации нельзя ограничиваться только определением ее размаха. Для анализа вариации необходим показатель, который отражает все колебания варьирующего признака и даёт обобщённую характеристик). Простейший показатель такого типа — среднее линейное отклонение. Среднее линейное отклонение ( абсолютных значений отклонений отдельных вариантов от их средней арифметической (при этом всегда предполагают, что среднюю вычитают из варианта: Среднее линейное отклонение: для несгруппированных данных
где n- число членов ряда; для сгруппированных данных
где В формулах (4.2) и (4.3) разности в числителе взяты по модулю, (иначе в числителе всегда будет ноль — "О" — алгебраическая сумма отклонений вариантов от их средней арифметической). Поэтому среднее линейное отклонение как меру вариации признака применяют в статистической практике редко (только в тех случаях, когда суммирование показателей без учета знаков имеет экономический смысл). С его помощью например, анализируется состав работающих, ритмичность производства, оборот внешней торговли. Дисперсия признака представляет собой средний квадрат отклонений вариантов от их средней величины, она вычисляется по формулам простой и взвешенной дисперсий (в зависимости от исходных данных): простая дисперсия для несгруппированных данных либо имеющих равные частоты:
взвешенная дисперсия для вариационного ряда с неравными частотами:
Техника вычисления дисперсии по формулам (6.2.4), (6.2.5) достаточно сложна, а при больших значениях вариантов и частот может быть громоздкой. Расчет можно упростить, используя свойства дисперсии (доказываемые в математической статистике): первое — если все значения признака уменьшить на одну и ту же
второе — если все значения признака уменьшить в одно и то же число раз (i раз), то дисперсия соответственно уменьшится в
третье-средний квадрат отклонений от любой величины А (отличной от средней арифметической) больше дисперсии признака на квадрат разности между средней арифметической и величиной А (свойство минимальности)
Используя свойства дисперсии, получим следующую формулу вычисления дисперсии в вариационных радах с равными интервалами по способу моментов:
где
(А — условный ноль, в качестве которого удобно использовать середину интервала, обладающего наибольшей частотой);
На основании последнего свойства дисперсии в случае когда А приравнивается нулю и, следовательно, не вычисляются отклонения, формула дисперсии примет вид:
Расчет дисперсии по вышеприведенной формуле менее трудоемок и может использоваться в рядах распределения с любым (равным и неравным) интервалом. Дисперсия имеет большое значение в экономическом анализе, В математической статистике важную роль для характеристики качества статистических оценок играет их дисперсия. Ниже, в частности, будет показано разложение дисперсии на соответствующие элементы,позволяющие оценить влияние различных факторов, обуславливающих вариацию признака; использование дисперсии для построения показателей тесноты корреляционной связи при оценке результатов выборочных наблюдений. Среднее квадратическое отклонение ( для несгруппированных данных
для вариационного ряда сгруппированных данных
Среднее квадратическое отклонение — это обобщающая характеристика размеров вариации признака в совокупности; оно показывает на сколько в среднем отклоняются конкретные варианты от их среднего значения; является абсолютной мерой колеблемости признака и выражается в тех же единицах, что и варианты, поэтому экономически хорошо интерпретируется. Среди множества варьирующих признаков существуют признаки, которыми одни единицы совокупности обладают, а другие не обладают. Такие признаки называются альтернативными. Примером таких признаков являются: наличие бракованной продукции, ученая степень у преподавателя, наличие академической задолженности у студента и др. Обозначим: 1 — наличие интересующего нас признака; 0 — его отсутствие: р — доля единиц, облагающих данным признаком; q — доля единиц, не обладающих данным признаком; тогда p+q=1. Исчислим среднее значение альтернативного признака и его дисперсию. Среднее значение альтернативного признака
так как р + q = 1. Следовательно, средняя арифметическая величина альтернативного признака равна доле единиц обладающих признаком. Дисперсии альтернативного признака.
Подставив в формулу дисперсии q = 1 -р, получим
Таким образом, Среднее квадратическое отклонение альтернативного признака
При вычислении средних величин и дисперсии для интервальных рядов распределения истинные значения признака заменяются центральными (серединными) значениями интервалов, которые отличаются от средней арифметической значений, включенных в интервал. Это приводит к появлению систематической погрешности при расчете дисперсии. В.Ф.Шеппард установил, что погрешность в расчете дисперсии, вызванная применением сгруппированных данных, составляет 1/12 квадрата величины интервала (T.e.i2/12), как в сторону занижения, так и в сторону завышения величины дисперсии. Поправка Шеппарда должна применяться, если распределение близко к нормальному, относится к признаку с непрерывным характером вариации, построено по большому количеству исходных данных (n >500), Однако исходя из того, что в ряде случаев обе погрешности, действуя в противоположны направлениях, нейтрализуются и компенсируют друг друга, можно иногда отказаться от введения поправок. Чем меньше значение дисперсии и среднего квадратического отклонения, тем однороднее совокупность и тем более типичной будет средняя величина. В статистической практике часто возникает необходимость сравнения вариаций различных признаков. Например, большой интерес представляет сравнение вариаций возраста рабочих и их квалификации, стажа работы и размера заработной платы, себестоимости и прибыли, стажа работы и производительности труда и т.д. Для подобных сопоставлений показатели абсолютной колеблемости признаков непригодны: нельзя сравнивать колеблемость стажа работы, выраженного в годах, с вариацией заработной платы, выраженной в рублях. Для осуществления такого рода сравнений, а также сравнений колеблемости одного и того же признака в нескольких совокупностях с различной средней арифметической используют относительный показатель вариации — коэффициент вариации. Относительные показатели вариации представляют собой отношение абсолютных показателей вариации к средней арифметической. Наиболее распространенными из них являются коэффициент вариации и линейный коэффициент вариации. Коэффициент вариации представляет собой выраженное в процентах отношение среднего квадратического отклонения к средней арифметической:
Линейный коэффициент вариации это отношение среднего линейного отклонения к средней арифметической:
Коэффициент вариации используют не только для сравнительной оценки вариации единиц совокупности, но и как характеристику однородности совокупности. Совокупность считается количественно однородной, если коэффициент вариации не превышает 33 %. Вариация признака обусловлена различными факторами, некоторые из этих факторов можно выделить, если статистическую совокупность разбить на группы по какому-либо признаку. Тогда, наряду с изучением вариации признака по всей совокупности в целом, становится возможным изучить вариацию для каждой из составляющих ее группы, а также и между этими группами. В простейшем случае, когда совокупность расчленена на группы по одному фактору, изучение вариации достигается посредством исчисления и анализа трех видов дисперсий: общей, межгрупповой и внутригрупповой. Общая дисперсия Межгрупповая дисперсия квадрату отклонений групповых (частных) средних
Внутригрупповая (частном) дисперсия группы
На основании внутригрупповых дисперсий по каждой группе, т.е. на основании
Согласно правилу сложения дисперсий общая дисперсия равна сумме средней из внутригрупповых и межгрупповой дисперсий:
Пользуясь правилом сложения дисперсий, можно всегда по двум известным дисперсиям определить третью - неизвестную, а также судить о силе влияния группировочного признака. В статистическом анализе широко используется эмпирический коэффициент детерминации ( s w:val="24"/><w:lang w:val="EN-US"/></w:rPr><m:t>Пѓ</m:t></m:r></m:e><m:sup><m:r><w:rPr><w:rFonts w:ascii="Cambria Math" w:fareast="Times New Roman" w:h-ansi="Times New Roman"/><wx:font wx:val="Cambria Math"/><w:i/><w:sz w:val="24"/><w:sz-cs w:val="24"/></w:rPr><m:t>2</m:t></m:r></m:sup></m:sSup></m:den></m:f></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>"> Эмпирический коэффициент детерминации показывает долю вариации результативного признака у под влиянием факторного признака х (остальная часть обшей вариации у обуславливается вариацией прочих факторов). При отсутствии связи эмпирический коэффициент детерминации равен нулю, а при функциональной связи — единице. Эмпирическое корреляционное отношение — это корень квадратный из эмпирического коэффициента детерминации:
оно показывает тесноту связи между группировочным и результативным признаками. Эмпирическое корреляционное отношение (η), как и ( Если связь отсутствует, то корреляционное отношение равно нулю, т.е. все групповые средние будут равны между собой, межгрупповой вариации не будет. Значит, группировочный признак никак не влияет на образование общей вариации. Если связь функциональная, то корреляционное отношение будет равно единице. В этом случае дисперсия групповых средних равна общей дисперсии ( Чем значение корреляционного отношения ближе к единице, тем теснее, ближе к функциональной зависимости связь между признаками. Для качественной оценки тесноты связи на основе показателя эмпирического корреляционного отношения можно воспользоваться соотношениями Чэддока: η, 0,1-0,3 0,3-0,5 0,5-0,7 0,7-0,9 0,9-0,99 Сила связи Слабая Умеренная Заметная Тесная Весьма тесная Решение т иповых задач к теме 1.6.: Показатели вариации. Задача № 1. По данным об урожайности винограда на различных участках определите: а) размах вариации; б) среднюю урожайность винограда; в) среднее линейное отклонение; г) дисперсию; д) среднее квадратическое отклонение; е)линейный коэффициент вариации.
Решение: а) размах вариации Р=Xmax-Xmin Р=10кг-Зкг=7 кг. б) средняя урожайность в) среднее линейное отклонение г) дисперсия д) среднее квадратическое отклонение е)линейный коэффициент вариации
Задача № 2. На основании нижеследующих данных определите: а) средний размер основных промышленно-производственных фондов на один завод (упрощенным способом); б) дисперсию (упрощенным способом); в) среднее квадратическое отклонение; г) коэффициент вариации.
Решение: Т.к. интервал группировки равный, для расчета используем упрощенный метод моментов (и для средней, и для дисперсии). а) средний размер основных фондов
где m1 момент первой степени
б) дисперсия
в) среднее квадратическое отклонение
г) коэффициент вариации
|

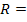 Xmax-Xmin (1.6.1.)
Xmax-Xmin (1.6.1.)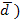 представляет собой среднюю арифметическую
представляет собой среднюю арифметическую ).
). (1.6.2)
(1.6.2)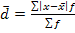 (1.6..3)
(1.6..3) - сумма частот вариационного рада.
- сумма частот вариационного рада.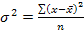 (1.6.4.)
(1.6.4.) (1.6.5.)
(1.6.5.)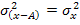
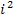 раз.
раз.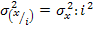
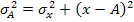
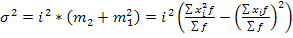 (1.6.6)
(1.6.6) — дисперсия, исчисленная по способу моментов; i — величина интервала;
— дисперсия, исчисленная по способу моментов; i — величина интервала; — новые (преобразованные) значения вариантов
— новые (преобразованные) значения вариантов - момент второго порядка; (1.6.7.)
- момент второго порядка; (1.6.7.)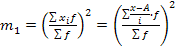 - квадрат момента первого порядка.(1.6.8.)
- квадрат момента первого порядка.(1.6.8.)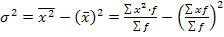 (1.6.9.)
(1.6.9.) ) равно корню квадратному из дисперсии:
) равно корню квадратному из дисперсии: (1.6.10.)
(1.6.10.) (1.6.11.)
(1.6.11.)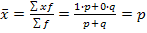 (1.6.12.)
(1.6.12.)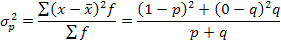
 (1.6.13.)
(1.6.13.)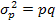 - дисперсия альтернативного признака равна произведению доли единиц, обладающих признаком, на долю единиц, не обладающих данным признаком.
- дисперсия альтернативного признака равна произведению доли единиц, обладающих признаком, на долю единиц, не обладающих данным признаком.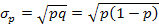 (1.6.14.)
(1.6.14.) (1.6.15.)
(1.6.15.) (1.6.16.)
(1.6.16.)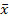 и может быть вычислена как простая дисперсия (по формуле (4.4) или взвешенная дисперсия по формуле (4,5).
и может быть вычислена как простая дисперсия (по формуле (4.4) или взвешенная дисперсия по формуле (4,5).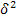 характеризует систематическую вариацию результативного порядка, обусловленную влиянием признака-фактора, положенного в основание группировки. Она равна среднему
характеризует систематическую вариацию результативного порядка, обусловленную влиянием признака-фактора, положенного в основание группировки. Она равна среднему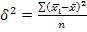 (1.6.17.)
(1.6.17.)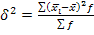 (1.6.18.)
(1.6.18.)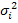 , отражает случайную вариацию, т.е. часть вариации, обусловленную влиянием неучтенных факторов и не зависящую от признака-фактора, положенного в основание группировки. Она равна среднему квадрату отклонений отдельных значений признака внутри группы х от средней арифметической этой
, отражает случайную вариацию, т.е. часть вариации, обусловленную влиянием неучтенных факторов и не зависящую от признака-фактора, положенного в основание группировки. Она равна среднему квадрату отклонений отдельных значений признака внутри группы х от средней арифметической этой (1.6.19.)
(1.6.19.)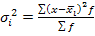 (1.6.20.)
(1.6.20.)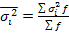 (1.6.21.)
(1.6.21.)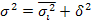 (1.6.22.)
(1.6.22.)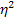 ) — показатель, представляющий собой долю межгрупповой дисперсии в общей дисперсии результативного признака и характеризующий силу влияния группировочного признака на образование общей вариации:
) — показатель, представляющий собой долю межгрупповой дисперсии в общей дисперсии результативного признака и характеризующий силу влияния группировочного признака на образование общей вариации: (1.6.23.)
(1.6.23.)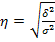 (1.6.24.)
(1.6.24.)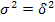 ), т.е. внутригрупповой вариации не будет. Это означает, что группировочный признак целиком определяет вариацию изучаемого результативного признака.
), т.е. внутригрупповой вариации не будет. Это означает, что группировочный признак целиком определяет вариацию изучаемого результативного признака. /
/
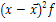
 (кг)
(кг)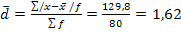 (кг)
(кг)
 (кг)
(кг)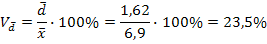
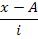 i=2
i=2
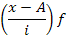
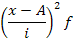

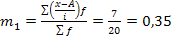 тогда,
тогда,  где m2 момент второй степени.
где m2 момент второй степени.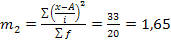 тогда
тогда 
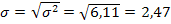 (млн. руб.).
(млн. руб.).


