Формальное описание комбинационных устройств числовыми последовательностямиОсновными способами задания собственных функций КЛС являются таблицы истинности или алгебраических выражений. Алгебраические формулы не являются инвариантными по отношению к базису, поэтому от такого способа следует отказаться. Таблицы истинности инвариантны по отношению к базису, но достаточно громоздки и неудобны. Можно договориться о том, чтобы все комбинации входных двоичных наборов в таблице истинности располагались в лексикографическом порядке, то есть в порядке монотонного возрастания от 0 до Рассматриваемая форма задания булевых функций, описывающих поведение логических схем, известна в литературе как векторная форма, которая, как уже было сказано выше, отличается от других известных форм компактностью и, что не менее важно, инвариантностью по отношению к используемому логическому базису. Пусть задана система логических функций (2.1):
Указанные функции описывают двоичный сумматор (рис. 2.3.).
Рис. 2.3. Двоичный сумматор
Определим все значения функций
Таблица 2.1 Таблица истинности двоичного сумматора
В рассматриваемом примере логическая последовательность функции переноса в старший разряд двоичного сумматора
а логическая последовательность функции суммы двоичного сумматора
Для более удобного восприятия в логическую последовательность через каждые четыре элемента можно вставлять служебный символ – пробел. В общем случае рассмотрим числовую последовательность, содержащую
Индекс Пусть
Двоичную запись числа Для того, чтобы определить значение логической функции на наборе значений аргументов Числовая последовательность не несёт никакой информации об именах аргументов логической функции. Но для целей синтеза это не важно. Важен лишь порядок старшинства входных переменных, а этот порядок устанавливается весами соответствующих разрядов во входном двоичном наборе. Поэтому аргументами мы будем считать весовые коэффициенты соответствующих им разрядов. В рассмотренном примере входную переменную Указанное выше обозначение входных переменных исключает путаницу при синтезе и анализе схем, поскольку однозначно определяет место соответствующего аргумента во входном наборе и старшинство входов относительно друг друга. Аналогичные обозначения можно применить и для выходов логических блоков и схем. В рассмотренном выше примере мы имеем систему (2.1) логических функций
Столбцы этой матрицы можно рассматривать как двоичные числа, которые для более компактной записи удобно перевести, например, в шестнадцатеричную систему счисления. Тогда матрица (2.3) запишется в виде числовой последовательности (2.4), которая полностью описывает функционирование двоичного сумматора:
Запись (2.4) компактнее минимальной дизъюнктивной нормальной формы (2.1). С помощью числовых последовательностей можно представлять и недоопределённые логические функции и их системы. Если система логических функций не определена на каком-либо наборе значений своих аргументов, то на соответствующем этому набору месте в числовой последовательности записывается специальный символ – «звёздочка» (*). Например, система логических функций, заданная последовательностью
не определена на наборах 011 и 101, так как третьему и пятому элементам указанной последовательности соответствуют звёздочки. Числовая последовательность, представляющая систему логических функций, не указывает имён этих функций. Поэтому порядок (старшинство) функций в системе можно характеризовать весами разрядов в двоичном представлении чисел последовательности. В последовательности (2.3), например, логическая функция
|

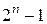 . При этом левая часть таблицы с расположенными в ней входными наборами будет одинаковой для всех функций
. При этом левая часть таблицы с расположенными в ней входными наборами будет одинаковой для всех функций  аргументов и её можно опустить. Оставшийся выходной столбец таблицы истинности для удобства необходимо транспонировать и записать в виде строки. Полученная таким образом числовая (логическая) последовательность будет полностью определять рассматриваемую систему логических функций
аргументов и её можно опустить. Оставшийся выходной столбец таблицы истинности для удобства необходимо транспонировать и записать в виде строки. Полученная таким образом числовая (логическая) последовательность будет полностью определять рассматриваемую систему логических функций  (2.1)
(2.1)
 – функция переноса в старший разряд,
– функция переноса в старший разряд, – функция суммы.
– функция суммы.

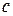
 ,
, .
. элементов:
элементов: . (2.2)
. (2.2) последовательно принимает значения от 0 до
последовательно принимает значения от 0 до  являются двоичной записью индекса
являются двоичной записью индекса 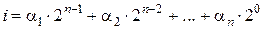 .
. в последовательности (2.2) заместить значением логической функции на наборе
в последовательности (2.2) заместить значением логической функции на наборе  , то мы получим числовую последовательность, которая однозначно представляет рассматриваемую логическую функцию. Например, двоичная последовательность
, то мы получим числовую последовательность, которая однозначно представляет рассматриваемую логическую функцию. Например, двоичная последовательность  представляет логическую функцию
представляет логическую функцию 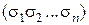 , необходимо двоичное число
, необходимо двоичное число 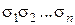 перевести в десятичную систему счисления и отсчитать нужный элемент в двоичной последовательности, причём счёт начинается с нуля. Пусть, например, требуется найти значение логической функции
перевести в десятичную систему счисления и отсчитать нужный элемент в двоичной последовательности, причём счёт начинается с нуля. Пусть, например, требуется найти значение логической функции 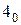 ,
,  , а
, а  . Для удобства старшинство переменных следует отсчитывать сверху вниз. Индекс «0» в обозначении переменной свидетельствует о том, что рассматриваемые сигналы являются входными для схемы.
. Для удобства старшинство переменных следует отсчитывать сверху вниз. Индекс «0» в обозначении переменной свидетельствует о том, что рассматриваемые сигналы являются входными для схемы. . (2.3)
. (2.3) . (2.4)
. (2.4)
 имеет вес 2, а функция
имеет вес 2, а функция 


