Метод наискорейшего спуска
Рассмотрим функцию φn (α) = f( x (n) - α g (n)) одной скалярной переменной α ³; 0 и выберем в качестве α n то значение, для которого выполняется равенство φn (α n) = Этот метод, предложенный в 1845 г. О. Коши, принято теперь называть методом наискорейшего спуска.
 На рис.3.6 изображена геометрическая иллюстрация этого метода для минимизации функции двух переменных. Из начальной точки x (0) перпендикулярно линии уровня f( x ) = f( x (0)) в направлении p (0) = - g (0) спуск продолжают до тех пор, пока не будет достигнуто минимальное вдоль луча x (0) - α p (0) (α > 0) значение функции f. В найденной точке x (1) этот луч касается линии уровня На рис.3.6 изображена геометрическая иллюстрация этого метода для минимизации функции двух переменных. Из начальной точки x (0) перпендикулярно линии уровня f( x ) = f( x (0)) в направлении p (0) = - g (0) спуск продолжают до тех пор, пока не будет достигнуто минимальное вдоль луча x (0) - α p (0) (α > 0) значение функции f. В найденной точке x (1) этот луч касается линии уровня f( x ) = f( x (1)). Затем из точки x (1) проводят спуск в перпендикулярном линии уровня направлении p (1) = - g (1) до тех пор, пока соответствующий луч не коснётся в точке x (2) проходящей через эту точку линии уровня, и т. д. Отметим, что на каждой итерации выбор шага α n предполагает решение задачи одномерной минимизации (3.13). Пример 3. Рассмотрим методнаискорейшего спуска для минимизации квадратичной функции f(x, y) = x2 + 2y2 – 4x – 4y Вектор-градиент для этой функции будет выглядеть следующим образом:
Для вычисления координат точки очередного приближения к точке минимума будут использоваться формулы x = x – α.G1(x,y) y = y – α.G2(x,y) Тогда функция φn (α), которую необходимо минимизировать на каждом шаге итерации для очередной точки с координатами (x, y), для данного случая имеет вид: FI(α, x, y) = (x – α.G1(x,y))2 + 2(y – α.G2(x,y))2 - 4(x – α.G1(x,y)) – 4(y – α.G2(x,y)) На рис.3.7 приведена блок-схема алгоритма основной программы метода наискорейшего спуска для минимизации рассмотренной в этом примере квадратичной функции f(x, y) = x2 + 2y2 – 4x – 4y. Входные данные: X, Y – координаты точки начального приближения из заданной области Х0 £ Х £ ХN, Y0 £ Y £YN; Eps – заданная точность вычислений; F(x, y) – заданная целевая функция – должна быть описана отдельно; G1(x, y) – функция - частная производная функции F(x, y) по переменной х; G2(x, y) – функция - частная производная функции F(x, y) по переменной y; Результаты: X, Y - приближение к искомым значениям координат точки минимума; F(X,Y) – значение целевой функции в точке минимума.
Начало
  < Eps < Eps
Рисунок 3.7 - Блок-схема алгоритма основной программы метода наискорейшего спуска для функции двух переменных
На рис.3.8 приведена блок-схема алгоритма процедуры MINALFA, осуществляющая поиск значения переменной α; > 0, при котором функция FI(α, x, y) принимает наименьшее значение при фиксированных значениях переменных х и y. В данном примере в процедуре MINALFA для решения одномерной задачи минимизации используется метод дихотомии. Входные параметры: X, Y – координаты точки очередного приближения к точке минимума; Eps – заданная точность вычислений; Выходные параметры: T – значение шага α; для вычисления очередного приближения к точке минимума; FI(α, x, y) – функция, для которой решается задача одномерной минимизации относительно переменной α; при фиксированных значениях переменных х и y.
MINALFA(X, Y, Eps, T)
  Alfa = (A + B)/2 – Eps/3 Alfa = (A + B)/2 – Eps/3
      FA £ FB FA £ FB
T = (A + B)/2
Рисунок 3.8 - Блок-схема алгоритма процедуры MINALFA
|

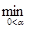 φn (α). (3.13)
φn (α). (3.13)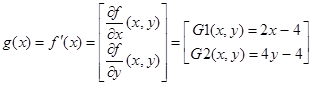


 Ввод Х, Y, Eps
Ввод Х, Y, Eps






 X1 = X
X1 = X

 Y = Y – Alfa.G2(Y)
Y = Y – Alfa.G2(Y)

 +
+ Вывод (X, Y), F(X, Y)
Вывод (X, Y), F(X, Y)
 end
end
 A = 0
A = 0


 Beta = (A + B)/2 + Eps/3
Beta = (A + B)/2 + Eps/3 FB = FI(Beta, X, Y)
FB = FI(Beta, X, Y)



 +
+
 end
end


