Использование дискретного преобразования ФурьеГлавный недостаток классического метода оценки спектральной плотности (метода Блэкмана-Тьюки) – большой объем вычислений. Гораздо меньше операций требуется при использовании прямого метода, основанного на использовании дискретного преобразования Фурье и современных вычислительных алгоритмах быстрого преобразования Фурье. При этом не нужно строить корреляционную функцию, а можно сразу найти спектральную плотность, обработав выборку значений исходного сигнала. В теории обработки аналоговых сигналов для перехода из временной области в частотную используется преобразование Фурье Оно имеет смысл для любой детерминированной (неслучайной) функции Для стационарного случайного процесса, не равного нулю, это условие никогда не будет выполняться, поэтому использовать преобразование Фурье в обычном смысле для анализа спектра случайных процессов нельзя. Однако если рассмотреть усеченный процесс
Квадрат модуля этой функции, деленный на ширину интервала
При реальных измерениях мы знаем только одну реализацию случайного процесса
Теперь остается найти (приближенно) Для оценки спектра в теории обработки сигналов обычно используют сетку частот (в герцах)
В теории управления принято строить спектры как функции угловой частоты (в радианах в секунду), которая получается из «обычной» частоты умножением на
Для частоты (4) где через
Заметим, что эта величина – комплексная, содержащая как вещественную, так и мнимую части. Легко подсчитать, что при расчете ДПФ по этим формулам для Для быстрого вычисления ДПФ были разработаны специальные алгоритмы, которые называются быстрым преобразованием Фурье (БПФ). Они позволили сократить количество операций с Казалось бы, формула (4) позволяет оценить спектр для всех частот вплоть до Согласно теореме Котельникова-Шеннона, по дискретным измерениям с периодом Подведем итог. Для оценки спектра сигнала по 1) с помощью БПФ (функция fft в Matlab) найти массив 2) взяв первую половину этого массива, рассчитать соответствующие значения 3) для каждой частоты Для сглаживания спектральной плотности так же, как и в методе Блэкмана-Тьюки, используются окна. Только теперь на весовую функцию умножается не оценка корреляционной функции, а сама реализация на интервале
Для этого случая окно Хэмминга на интервале
Далее дискретное преобразования Фурье вычисляется для отсчетов взвешенной функции, то есть, вместо (4) получаем
Использование окна для исходного сигнала приводит к уменьшению его энергии и, как следствие, к заниженным оценкам спектральной плотности. Чтобы скомпенсировать эти потери, весовая функция умножается на дополнительный коэффициент Несложно подсчитать, что для окна Хэмминга из этого условия следует:
|

 .
. , которая абсолютно интегрируема, то есть интеграл от ее модуля на всей оси сходится:
, которая абсолютно интегрируема, то есть интеграл от ее модуля на всей оси сходится:  .
.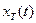 , равный реализации
, равный реализации 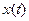 случайного процесса на интервале
случайного процесса на интервале  и нулю вне этого интервала, для него можно найти преобразование Фурье:
и нулю вне этого интервала, для него можно найти преобразование Фурье: .
. , характеризует среднюю мощность сигнала на частоте
, характеризует среднюю мощность сигнала на частоте  . В пределе, при
. В пределе, при 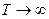 , мы должны получить спектральную плотность мощности. Так как
, мы должны получить спектральную плотность мощности. Так как  .
. , поэтому усреднение по ансамблю чаще всего невозможно. Тогда для оценки спектральной плотности можно использовать предыдущую формулу без усреднения:
, поэтому усреднение по ансамблю чаще всего невозможно. Тогда для оценки спектральной плотности можно использовать предыдущую формулу без усреднения: , где
, где 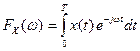 .
. по дискретным измерениям процесса
по дискретным измерениям процесса  при
при  для
для  , так что интервал
, так что интервал  подынтервалов шириной
подынтервалов шириной  (поэтому
(поэтому  ). Тогда интегрирование можно приближено заменить суммой:
). Тогда интегрирование можно приближено заменить суммой:  .
. с шагом
с шагом  .
.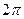 :
: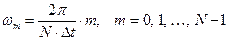 .
.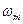 получаем
получаем 
 ,
, обозначена сумма, называемая дискретным преобразованием Фурье (ДПФ):
обозначена сумма, называемая дискретным преобразованием Фурье (ДПФ): .
. (обозначается
(обозначается  ). Это значит, что если
). Это значит, что если  . В функции fft среды Matlab используется модификация алгоритма БПФ, предложенного Дж. Кули и Дж. Тьюки. Этот алгоритм наиболее эффективен, если число отсчетов
. В функции fft среды Matlab используется модификация алгоритма БПФ, предложенного Дж. Кули и Дж. Тьюки. Этот алгоритм наиболее эффективен, если число отсчетов  при целом
при целом  ). Заметим, что если это не так, всегда можно дополнить ряд нулями до ближайшей степени двойки.
). Заметим, что если это не так, всегда можно дополнить ряд нулями до ближайшей степени двойки. . Однако нужно учесть, что для анализа мы используем только дискретные измерения с периодом
. Однако нужно учесть, что для анализа мы используем только дискретные измерения с периодом  (или до соответствующей угловой частоты
(или до соответствующей угловой частоты  , которая называется частотой Найквиста [33]). Поэтому только оценка спектра на частотах
, которая называется частотой Найквиста [33]). Поэтому только оценка спектра на частотах 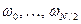 дает нам практически полезную информацию[34].
дает нам практически полезную информацию[34].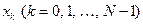 нужно выполнить следующие действия:
нужно выполнить следующие действия: ;
; для частот, не превышающих частоту Найквиста
для частот, не превышающих частоту Найквиста  ;
;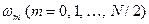 найти оценку спектральной плотности мощности по формуле:
найти оценку спектральной плотности мощности по формуле:  .
.


 .
. , где
, где  .
. , который определяется из условия нормировки (сохранения энергии весовой функции окна, которая должна остаться такой же, как для прямоугольного окна):
, который определяется из условия нормировки (сохранения энергии весовой функции окна, которая должна остаться такой же, как для прямоугольного окна):  .
.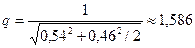 .
.


