Неопределенный интеграл
Пример 1. Найти интеграл Решение. Поделив каждое слагаемое числителя подынтегральной дроби на знаменатель, и используя, что интеграл от суммы функций равен сумме интегралов от этих функций, получим:
Первый интеграл является табличным: Во втором интеграле воспользуемся тем, что Получим следующую запись Если представить, что arcsinx=t, то данный интеграл будет интегралом от степени
Таким образом, для заданного интеграла имеем:
Пример 2. Найти интеграл
Решение. Как и в примере 1, вычислим дифференциал Числитель подынтегральной дроби
Разделив почленно подынтегральную функцию, получим:
Первый интеграл это интеграл вида
Для того чтобы вычислить второй интеграл, выделим полный квадрат из выражения (
С учетом того, что
Таким образом, для заданного интеграла имеем:
Пример 3. Найти интеграл
Решение. Воспользуемся формулой интегрирования по частям:
В выражении, стоящем под знаком интеграла, обозначим: По данным
Составляем правую часть формулы интегрирования по частям, записывая вместо
Пример 4. Найти интеграл Решение. Отделим от нечетной степени один множитель: Если положить
Возвратившись к прежней переменной, получаем:
Пример 5. Найти интеграл Решение. Понизим у Тогда в исходном интеграле получим следующее:
Первый интеграл является табличным:
Пример 6. Найти интеграл Решение. С помощью формул тригонометрии:
а интеграл приобретает следующий вид:
Применив универсальную тригонометрическую замену
Возвратившись к прежней переменной, имеем:
Пример 7. Найти интеграл Решение. Разложим подынтегральную функцию на сумму простейших дробей. Чтобы разложить знаменатель на сомножители нужно решить квадратное уравнение
Тогда наша дробь представима в виде суммы элементарных дробей:
Нужно найти неизвестные коэффициенты A,B,C. Для этого приведем дроби к общему знаменателю:
Так как дроби между собой равны, а также равны их знаменатели, то и числители также равны. Поэтому у многочленов, стоящих в числителе приравняем коэффициенты при х2,х1,х0 и получим систему трех уравнений с тремя неизвестными:
Решив эту систему получим следующие значения A, B и C: Значит, наша дробь раскладывается на сумму дробей:
Подставляя это разложение в интеграл, получаем:
Пример 8. Найти интеграл Решение. Для того, чтобы избавиться от иррациональности в подынтегральном выражении, нужно сделать следующую замену:
Тогда данный интеграл запишем в виде:
Подынтегральное выражение представляет собой неправильную дробь, в которой нужно выделить целую часть путем деления многочлен на многочлен: Возвращаясь к интегралу, получим:
|

 .
.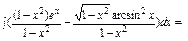
 .
. .
. .
.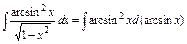 .
. , но явно переходить к переменной t нет необходимости.
, но явно переходить к переменной t нет необходимости. .
. .
. .
. .
.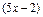 преобразуем тождественно к виду, содержащему
преобразуем тождественно к виду, содержащему  .
.  Исходя из преобразований, сделанных выше, получаем:
Исходя из преобразований, сделанных выше, получаем: .
.
 .
.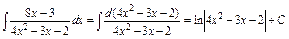 .
. ):
): Второй инте грал теперь будет иметь следующий вид:
Второй инте грал теперь будет иметь следующий вид: .
. , этот интеграл табличный.
, этот интеграл табличный.
 .
. .
. .
. , а
, а 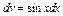 .
.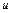 и
и  , для составления правой части формулы, вычисляем
, для составления правой части формулы, вычисляем  и
и 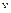 :
: ,
,  .
.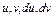 их выражения.
их выражения.
 .
. .
. , то
, то  . Перейдем в интеграле к новой переменной t:
. Перейдем в интеграле к новой переменной t: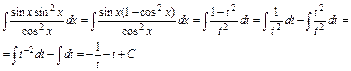
 .
. .
. и
и  степень с помощью следующих формул:
степень с помощью следующих формул:  .
.
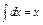 , а во втором интеграле применим формулу понижения степени. Тогда искомый интеграл преобразуется к виду:
, а во втором интеграле применим формулу понижения степени. Тогда искомый интеграл преобразуется к виду: .
. .
. , такие подынтегральные выражения приводятся к рациональным выражениям, зависящим от
, такие подынтегральные выражения приводятся к рациональным выражениям, зависящим от  . Получаем:
. Получаем: ,
, .
. , получим интеграл
, получим интеграл 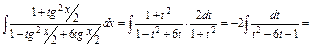
 .
. .
.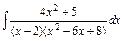 .
. . Его корнями являются
. Его корнями являются  . Теперь знаменатель может быть представлен следующим образом
. Теперь знаменатель может быть представлен следующим образом .
. .
. .
. .
. .
. .
.
 .
.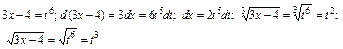

 .
.



