Задача Коши. Метод Эйлера
Одношаговые методы решения задачи Коши
Содержание
8.1. Задача Коши. Метод Эйлера. 2
8.2. Неявный метод Эйлера. 5
8.3. Погрешности метода решения. 6
8.4. Модифицированные методы Эйлера. 8
8.5. Правило Рунге. 9
8.6. Методы Рунге-Кутта. 11
8.7. Метод Рунге-Кутта-Фельберга. 13
Упражнения. 13
Вопросы для повторения. 14
Задача Коши или начальная задача состоит в нахождении решения дифференциального уравнения при заданном начальном условии:
Пусть Определение. Функция
где L – постоянная, не зависящая ни от Теорема Коши. Пусть в уравнении Метод Эйлера состоит в том, что интегральная кривая, являющаяся решением задачи, приближенно заменяется некоторой ломаной линией – ломаной Эйлера. Пусть требуется найти решение задачи Коши на отрезке
Метод Эйлера описывается формулой
На каждом шаге истинная интегральная кривая заменяется отрезком касательной. Получаем в итоге линию, называемую ломаной Эйлера. Из теории дифференциальных уравнений известно утверждение: начальная задача (8.1) эквивалентна интегральному уравнению
При решении начальной задачи на отрезке от
и требуется приближенно описать интеграл на отрезке Иначе метод Эйлера можно получить, разложив решение в ряд Тейлора и ограничившись только линейными слагаемыми ряда:
 (8.6) (8.6)
Пример 8.1. Ломаная Эйлера для решения задачи Коши:
Сформулируем задачу Коши для системы уравнений. Система уравнений первого порядка, разрешенных относительно производных
называется нормальной системой. Введя векторные функции
Задача Коши состоит в решении системы дифференциальных уравнений (8.8) при заданном начальном условии Пример 8.2. Найдем решение задачи Коши:
Эта задача легко решается аналитически. Можно также найти решение в среде Matematica, выполнив команду: In[]:= DSolve[{y'[x]==-3 y[x]+z[x], z'[x]==y[x]-3 z[x], y[0]==1, z[0]==3}, {y[x], z[x]}, x]//Expand Получаемый ответ: Out[]= Решение методом Эйлера в среде Mathcad дано на рис. 8.3. Уравнения интегрируются на отрезке
Уравнение n -го порядка, разрешенное относительно старшей производной, имеет вид:
Такое уравнение легко свести к нормальной системе. Для этого введем обозначения:
Получим в результате систему уравнений первого порядка для неизвестных Пример 8.3 Частный случай уравнения колебаний имеет вид: Преобразуем уравнение к нормальной системе уравнений:
На рис. 8.4 показано решение методом Эйлера в системе Mathcad. В матрице Y строка Y0 включает значения независимой переменной, строка Y1 содержит значения V, строка Y2 включает значения Z.
|

 (8.1)
(8.1) – некоторый прямоугольник в плоскости
– некоторый прямоугольник в плоскости  с центром в точке
с центром в точке  .
. удовлетворяет в прямоугольнике
удовлетворяет в прямоугольнике  , если в этом прямоугольнике
, если в этом прямоугольнике , (8.2)
, (8.2) , ни от
, ни от  функция
функция  в прямоугольнике
в прямоугольнике  , существует единственное решение начальной задачи
, существует единственное решение начальной задачи 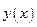 не выходит за пределы прямоугольника
не выходит за пределы прямоугольника  ; иными словами введем на отрезке сетку точек:
; иными словами введем на отрезке сетку точек:  . Будем искать приближенное решение задачи в узлах сетки. Введем обозначения:
. Будем искать приближенное решение задачи в узлах сетки. Введем обозначения: – приближенные значения решения в узлах сетки;
– приближенные значения решения в узлах сетки; ;
; – шаг приращения аргумента – шаг сетки;
– шаг приращения аргумента – шаг сетки; – максимальное значение шага (в частном случае сетка может быть равномерной
– максимальное значение шага (в частном случае сетка может быть равномерной 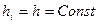 ).
). (8.3)
(8.3) (8.4)
(8.4) до
до  интегральное равнение (8.4) принимает вид:
интегральное равнение (8.4) принимает вид: , – (8.5)
, – (8.5)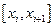 .
.
 – показана на рис.8.2.
– показана на рис.8.2.
 (8.7)
(8.7) ,
,  , можно записать систему (8.7) в векторной форме
, можно записать систему (8.7) в векторной форме . (8.8)
. (8.8) .
.
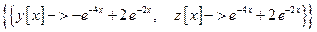 .
. . Шаг приращения аргумента выбирается равным
. Шаг приращения аргумента выбирается равным 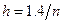 , где
, где  – число точек на отрезке. Так же, как и в примере 8.1 метод Эйлера записывается в векторной форме. В результате расчетов получаем матрицу, первая строка которой дает приращение
– число точек на отрезке. Так же, как и в примере 8.1 метод Эйлера записывается в векторной форме. В результате расчетов получаем матрицу, первая строка которой дает приращение  . На графиках показаны ломаные Эйлера и истинные интегральные кривые. Если уменьшить шаг приращения аргумента, например, положить
. На графиках показаны ломаные Эйлера и истинные интегральные кривые. Если уменьшить шаг приращения аргумента, например, положить  , то погрешность решения уменьшается. И наоборот, если положить
, то погрешность решения уменьшается. И наоборот, если положить  (
( ), то погрешность значительно увеличивается: процесс, описываемый приближенным решением, становится, вообще, немонотонным.
), то погрешность значительно увеличивается: процесс, описываемый приближенным решением, становится, вообще, немонотонным.
 (8.9)
(8.9) . (8.10)
. (8.10) .
. , где a – коэффициент затухания. Зададим начальные условия:
, где a – коэффициент затухания. Зададим начальные условия:  . Решение данной задачи Коши представляет собой затухающую косинусоиду.
. Решение данной задачи Коши представляет собой затухающую косинусоиду. .
.



