Краткая теория. 1.1.Закрепление лекционного материала по теории теплопроводнТЕПЛОФИЗИЧЕСКИЙ СПЕЦПРАКТИКУМ Работа №11
РАСЧЕТ ФАКТОРОВ ПРОЦЕССА ТЕПЛОПРОВОДНОСТИ ПРИ ОХЛАЖДЕНИИ ПЛАСТИНЫ
Цель работы 1.1.Закрепление лекционного материала по теории теплопроводности. 1.2. Приобретение навыка расчета сложных функций, определяющих расход тепла, а также использования графика зависимости θ = f (Fo, Bi).
Краткая теория Рассматривается процесс нестационарной теплопроводности в неограниченной пластине толщиной Уравнение нестационарной теплопроводности для бесконечной пластины имеет вид:
где Начальные условия: Граничные условия 3-го рода: при при Граничные условия 3-го рода имеют следующий физический смысл: количество теплоты, подходящее к поверхности пластины за счёт теплопроводности, отдаётся в окружающую среду за счёт теплоотдачи по закону Ньютона. Начало координат помещается в середине пластины. Задача симметричная. Введём безразмерные переменные:
Уравнение теплопроводности примет вид:
Здесь Граничные условия в безразмерных переменных будут: при при Здесь Начальные условия: при Уравнение решается методом разделения переменных, решение ищется в виде произведения двух функций – только от координаты и только от времени:
Подставим (4) в (3):
Левая часть равенства (5) зависит только от
Отсюда получаем систему двух уравнений:
Решением первого уравнения является экспоненциальная функция:
Постоянная р выбирается из физических соображений. Для тепловых процессов, стремящихся к температурному равновесию, когда по истечении длительного промежутка времени ( Частное решение второго уравнения системы (6) - гармоническая функция:
Тогда решение уравнения (4) будет иметь вид:
Так как задача симметричная, в решении должна быть только чётная функция ( Из граничных условий находим μ: при Подставим в граничные условия формулу (7), (учитывая, что В = 0):
Отсюда получаем характеристическое уравнение:
которое решается, например, графически. Из анализа этого тригонометрического уравнения следует, что при каждом значении Тогда выражение для
Коэффициенты при
Используем вспомогательные интегралы:
Помножим левую и правую части формулы (9) на
Тогда имеем:
В итоге решение уравнения (3) примет вид:
|

 . Начальная температура пластины постоянна по всему сечению,
. Начальная температура пластины постоянна по всему сечению,  . В начальный момент времени пластина помещается в среду с постоянной температурой
. В начальный момент времени пластина помещается в среду с постоянной температурой 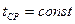 ,
, 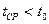 . Между ограничивающими поверхностями и окружающей средой происходит теплообмен по закону Ньютона. Требуется найти распределение температуры по толщине пластины, а также удельный тепловой поток.
. Между ограничивающими поверхностями и окружающей средой происходит теплообмен по закону Ньютона. Требуется найти распределение температуры по толщине пластины, а также удельный тепловой поток. ,
, 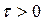 ,
, 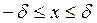 , (1)
, (1)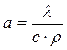 - коэффициент температуропроводности, λ; – коэффициент теплопроводности материала, с, ρ; - его удельная теплоёмкость и плотность соответственно.
- коэффициент температуропроводности, λ; – коэффициент теплопроводности материала, с, ρ; - его удельная теплоёмкость и плотность соответственно.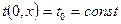 ,
, 
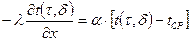 ,
,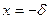
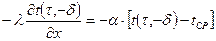 .
. ,
, 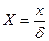 . (2)
. (2) . (3)
. (3) - критерий Фурье – безразмерное время в задачах нестационарной теплопроводности. Критерий Фурье характеризует соотношение между скоростью изменения тепловых условий в окружающей среде и скоростью перестройки поля температуры внутри рассматриваемого тела, которая зависит от размеров тела и коэффициента его температуропроводности а.
- критерий Фурье – безразмерное время в задачах нестационарной теплопроводности. Критерий Фурье характеризует соотношение между скоростью изменения тепловых условий в окружающей среде и скоростью перестройки поля температуры внутри рассматриваемого тела, которая зависит от размеров тела и коэффициента его температуропроводности а.
 ,
,
 .
.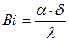 - критерий Био- критерий краевого подобия (
- критерий Био- критерий краевого подобия (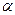 - коэффициент теплоотдачи с поверхности тела в окружающую среду).
- коэффициент теплоотдачи с поверхности тела в окружающую среду).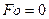
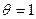 .
.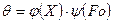 . (4)
. (4)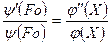 . (5)
. (5)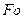 , т.е. от времени τ;, или может быть постоянной, но не зависит от координаты. Правая часть зависит только от координаты или может быть постоянной, но не зависит от времени. Равенство (5) должно выполняться при любых значениях координаты и времени. Это возможно только в том случае, если правая и левая части равенства равны некоторой постоянной величине р.
, т.е. от времени τ;, или может быть постоянной, но не зависит от координаты. Правая часть зависит только от координаты или может быть постоянной, но не зависит от времени. Равенство (5) должно выполняться при любых значениях координаты и времени. Это возможно только в том случае, если правая и левая части равенства равны некоторой постоянной величине р. .
.
 ,
,  .
.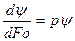 ,
,  ,
,  ,
,  ,
, 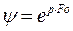 .
. ) должно установиться определённое распределение температуры, р должно быть отрицательной величиной. Если
) должно установиться определённое распределение температуры, р должно быть отрицательной величиной. Если  , то при длительном промежутке времени температура будет больше любой наперёд заданной величины, т.е.
, то при длительном промежутке времени температура будет больше любой наперёд заданной величины, т.е.  , что противоречит физическому смыслу задачи. Итак,
, что противоречит физическому смыслу задачи. Итак,  . Тогда
. Тогда  .
.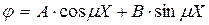 .
.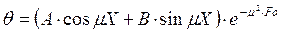 . (7)
. (7)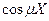 ), следовательно, В = 0.
), следовательно, В = 0.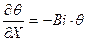 .
.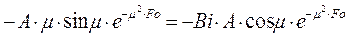 .
. ,
,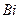 существует бесконечное множество решений;
существует бесконечное множество решений; 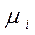 - корни характеристического уравнения.
- корни характеристического уравнения.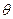 примет вид:
примет вид: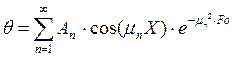 . (8)
. (8)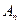 в выражении (8) находятся из начальных условий:
в выражении (8) находятся из начальных условий: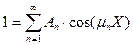 . (9)
. (9)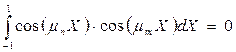 при
при  ,
, при
при  .
. и проинтегрируем от -1 до 1. От суммы останется одно слагаемое, когда m = n:
и проинтегрируем от -1 до 1. От суммы останется одно слагаемое, когда m = n: .
.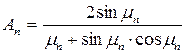 . (10)
. (10)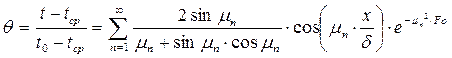 . (11)
. (11)


