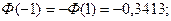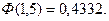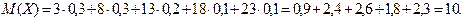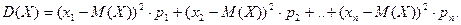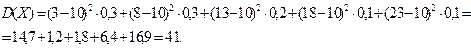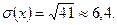Тема 8. Определенный интеграл
Литература: [3], гл.XIV, §1-11, упр.2,7, гл.XV,§1-7, упр.1, 6,18.
Задача 9. Вычислить определенные интегралы:
а)
Решение.
Для вычисления определенных интегралов применяют формулу Ньютона-Лейбница:
а)
б) Вычислим данный интеграл методом подстановки. С учетом новых пределов интегрирования по переменной t получим:
в)
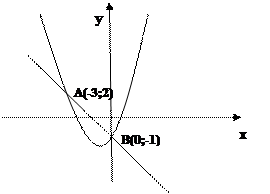
Задача 10. Вычислить площадь фигуры, ограниченной параболой
Решение. Площадь S фигуры, ограниченной снизу кривой Найдем точки пересечения параболы и прямой, решив систему уравнений:
Значит, парабола и прямая пересекаются в точках А(-3;2) и В(0;- 1) (см.рис.3)
рис.3 Подставив в формулу (***)
Вопросы для самопроверки
1. Что называется определенным интегралом от функции у= f(х) на отрезке [а; b]? 2. Каков геометрический смысл определенного интеграла? 3. Назовите свойства определенного интеграла. 4. Напишите формулу Ньютона-Лейбница. 5. Напишите формулу интегрирования по частям в определенном интеграле.
Тема 9. Основные понятия теории вероятностей
Литература:(1),гл.I,1-3;(4),ч.II,гл.1,§1,2.
К числу основных понятий теории вероятностей относятся такие как испытание, событие, вероятность события, относительная частота появления события в испытаниях. Событие – это результат (исход) испытания. Вероятность – это число, характеризующее степень возможности появления события. Каждый из возможных исходов испытания называется элементарным исходом. Исходы, в которых интересующее событие А наступает, называются благоприятными этому событию. Вероятность события А – это отношение числа благоприятных исходов испытания к числу элементарных исходов испытания: Все исходы должны быть равновозможными, единственно возможными и несовместными. Относительная частота события А – это отношение числа испытаний, в которых событие А наступило к общему числу проведенных испытаний:
Хотя по внешнему виду формулы для вычисления вероятности и относительной частоты одинаковы, сами эти понятия не тождественны. Различие между вероятностью и относительной частотой состоит в том, что вероятность вычисляют до опыта, а относительная частота может быть вычислена лишь после того, как опыт будет произведен. Важным свойством относительной частоты является ее устойчивость. Это свойство состоит в том, что при многократных повторениях испытаний относительные частоты группируются около некоторого постоянного числа, которое и принимают за статистическую вероятность события. Задача 11. В ящике из 80 одинаковых деталей для комбайнов, полученных колхозом, 8 деталей нестандартных. Какова вероятность того, что наугад взятая деталь окажется стандартной? Решение. Обозначим через А событие - «взятая наугад деталь стандартная». Всего деталей 80, поэтому общее число возможных элементарных исходов n=80. Эти исходы единственно возможные (одна деталь взята обязательно) и равновозможные (деталь взята наудачу). Благоприятствуют событию А лишь 72 исхода (72 детали стандартных). Искомая вероятность равна отношению числа исходов, благоприятствующих событию, к числу всех элементарных исходов: Задача 12. Из 25 посаженных деревьев прижилось 20. Определить относительную частоту прижившихся деревьев. Решение. Обозначим через А событие - «посаженное дерево прижилось». Относительная частота прижившихся деревьев равна Вопросы для самопроверки
1. Что называется событием? Приведите примеры событий. 2. Какие события называются достоверными, невозможными, случайными? Приведите примеры этих событий. 3. Какие события называются несовместными, совместными? Приведите примеры. 4. Какие события называются элементарными или случайными? 5. Сформулируйте классическое определение вероятности события. Укажите возможные границы вероятности. 6. Что такое относительная частота появления события? 7. В чем состоит различие между вероятностью и относительной частотой? 8. В чем состоит свойство устойчивости относительной частоты? 9. Приведите статистическое определение вероятности события. Тема 10. Основные теоремы теории вероятностей
Литература:(1).гл.II,упр.1,2.гл.III,упр.1-3,6,гл.IV,§1-2,упр.1,3-6;(4),ч.II,гл.1,§3-4,упр.6,7,10.
Для того чтобы усвоить теорему сложения вероятностей, надо сначала уяснить понятие суммы событий, а также различие между событиями совместными и несовместными.
События А и В называются несовместными, если появление одного из них исключает возможность появления другого в одном и том же испытании.
События А и В называются совместными, если в одном и том же испытании они могут появиться вместе.
Суммой двух событий А и В называется событие А+В, состоящее в появлении события А, или события В, или обоих этих событий. В частности, если два события несовместные, то их сумма – это событие, состоящее в появлении только одного из них, безразлично какого.
Теорема сложения вероятностей несовместных событий: вероятность появления одного из двух несовместных событий А или В равна сумме вероятностей этих событий:
Теорема сложения вероятностей совместных событий: вероятность появления хотя бы одного из двух совместных событий равна сумме вероятностей этих событий без вероятности их совместного появления:
Перед изучением теорем умножения вероятностей надо усвоить определение произведения событий и различие между событиями зависимыми и независимыми.
Событие А называется зависимым от события В, если вероятность появления события А зависит от того, произошло или не произошло событие В.
Событие А называется независимым от события В, если вероятность появления события А не зависит от того, произошло или не произошло событие В.
Произведением событий А и В называется событие АВ, состоящее в одновременном появлении этих событий: и события А и события В.
Теорема умножения вероятностей зависимых событий: вероятность совместного появления двух зависимых событий равна произведению вероятности одного из них на условную вероятность другого, вычисленную в предположении, что первое событие уже произошло Теорема умножения вероятностей независимых событий: вероятность совместного появления двух независимых событий равна произведению вероятностей этих событий:
Теорема (Формула полной вероятности): вероятность события А, которое может наступить лишь при условии появления одного из несовместных событий
Задача 13. В денежно-вещевой лотерее на серию в 1000 билетов приходится 120 денежных и 80 вещевых выигрышей. Какова вероятность какого-либо выигрыша на один лотерейный билет? Решение. Пусть событие А-денежный выигрыш на один лотерейный билет, событие В - вещевой выигрыш на этот же билет. Найдем вероятность этих событий: Пусть событие С–какой-либо выигрыш на один лотерейный билет. Очевидно, С=А+В, причем события А и В несовместны. Применяя теорему сложения вероятностей несовместимых событий, получим Р(С)=Р(А+В)=Р(А)+Р(В)=0,12+0,08=0,2.
Задача 14. Вероятность выживания одного организма в течение 20 минут Р=0,9. В пробирке с благоприятными для существования этих организмов условиями находятся только что родившиеся два организма. Какова вероятность того, что через 20 минут они будут живы? Решение. Пусть событие А- первый организм жив через 20 минут, событие В- второй организм жив через 20 минут. Будем считать, что между организмами нет внутривидовой конкуренции, т.е. события А и В независимы. Событие, что оба организма живы, есть событие С=АВ. По теореме умножения вероятностей независимых событий получим Задача 15. Студент знает 20 из 25 вопросов программы. Найти вероятность того, что студент знает предложенные ему экзаменатором два вопроса. Решение. Пусть событие А- студент знает первый предложенный ему вопрос; событие В- студент знает второй предложенный ему вопрос. Тогда вероятность того, что студент знает первый, предложенный ему вопрос, равна Вероятность того, что студент знает второй, предложенный ему вопрос при условии, что он знает и первый предложенный вопрос, равна Пусть событие С - студент знает оба предложенных ему вопроса. Событие С состоит в том, что наступит и событие А, и событие В, т.е. С=АВ. Т.к. события А и В зависимы, то по теореме умножения вероятностей зависимых событий получим Задача 16. Всхожесть семян одного вида растений оценивается вероятностью 0,8, другого вида растений - вероятностью 0,7. Посажено по одному семени каждого вида растений. Найти вероятность того, что взойдет хотя бы одно семя. Решение. Пусть событие А - взойдет семя первого вида растений, событие В- взойдет семя второго вида растений. По условию задачи Р(А)=0,8, Р(В)=0,7. Обозначим через С - событие, состоящее в том, что из посеянных семян взойдет хотя бы одно. Очевидно, С= А+В, причем события А и В – совместные и независимые. По теореме сложения вероятностей совместных событий получим
Вопросы для самопроверки 1. Что понимается под суммой двух событий? Приведите примеры. 2. Сформулируйте теорему сложения вероятностей для несовместных событий. 3. Что понимается под полной группой событий? Чему равна сумма вероятностей событий, составляющих полную группу? 4. Какие события называются противоположными? Чему равна сумма вероятностей противоположных событий? 5. Какие события называются независимыми, зависимыми? Приведите примеры. 6. Что называется условной вероятностью события? 7. Что понимается под произведением двух событий? Приведите примеры. 8. Сформулируйте теоремы умножения вероятностей для независимых и зависимых событий. 9. Сформулируйте теорему сложения вероятностей для совместных событий. 10. Приведите формулу полной вероятности.
Тема 11. Повторение испытаний Литература: (1), гл.V§1-4, упр.1-3, 5, 7, 8, гл.VI, §5, упр.4:(4).ч.II,гл.II, §5-8, упр.1-13.
Пусть проводится n независимых испытаний, в каждом из которых вероятность наступления события А одинакова и равна p, а значит, вероятность ненаступления события А в каждом испытании также одинакова и равна q=1-р. Тогда вероятность того, что в n испытаниях событие А наступит ровно к раз вычисляют по формуле Бернулли:
Если n велико
Значения этой функции затабулированы в приложении 1. Если же n большое число
При решении практических задач иногда важно определить вероятность того, что событие наступит не менее
Задача 22. Всхожесть семян данного сорта растений оценивается вероятностью а) пять всходов; б) не менее пяти всходов; в) не менее двух всходов.
Решение. а) По условию задачи n=6, k=5,
Подставим эти данные в формулу Бернулли:
б) Пусть событие А – из 6 семян будет не менее 5 всходов. Это событие А состоит из двух событий: 1) из 6 семян будет 5 всходов; 2) из 6 семян будет 6 всходов. По теореме вероятностей несовместных событий искомая вероятность будет равна: Первое слагаемое найдено в предыдущем пункте. Второе слагаемое тоже определим по формуле Бернулли: (при этом надо иметь в виду, что 0!=1).
Следовательно,
в) Пусть событие А - из 6 семян будет не менее 2 всходов, т. е. или 2 всхода, или 3 всхода, или 4 всхода, или 5 всходов, или 6 всходов. Тогда событием На основании теоремы сложения вероятностей не совместных событий: Вероятности
Значит, По свойству вероятности противоположных событий следовательно,
Задача 23. Вероятность прорастания семян данного сорта растений равна 0,75. Посеяно 300 семян. Найти наивероятнейшее число всходов. Решение. Наивероятнейшее число n - число всех испытаний; р - вероятность появления события в одном испытании; q - вероятность непоявления события в одном испытании. По условию задачи р=0,75; q=0,25; n=300. Тогда Так как
Задача 24. Завод сортовых семян выпускает гибридные семена кукурузы. Известно, что семена первого сорта составляют 90%. Определить вероятность того, что из взятых наудачу для проверки 400 семян 354 будут семенами первого сорта.
Решение. Если производится большое число n независимых испытаний в каждом из которых вероятность наступления события А постоянна и равна р, то вероятность Дано: Найдем Используя помещенное в таблице 1 приложение значений функции По формуле
Задача 25. Вероятность того, что зерно заражено вредителями, равна 0,002. Найти вероятность того, что из 2000 зерен окажется не более двух зараженных зерен. Решение. Пусть событие А – из 2000 зерен окажется не более двух зараженных зерен. Это событие состоит из трех событий: 1) Из 2000 зерен зараженных будет 2 зерна; 2) Из 2000 зерен зараженных будет 1 зерно; 3) Из 2000 зерен зараженных зерен не будет. По теореме сложения вероятностей не совместных событий искомая вероятность будет равна: Так как n=2000 достаточно велико, а вероятность наступления события в каждом из n независимых испытаний достаточно мала р=0,002, то вероятность
Задача 26. Принимая вероятность вызревания кукурузного стебля с тремя початками равной 0,8, найти вероятность того, что среди 2500 стеблей опытного участка число указанных стеблей будет от 1980 до 2030.
Решение.
Если вероятность наступления события А в каждом из n независимых испытаний постоянна и равна р, а число n достаточно велико, то вероятность того, что событие А в этих испытаниях наступит не менее По условию задачи n= 2500; р=0,8; q= 0,2;
Используя помещенное в таблице 2 приложение значений функции
Вопросы для самопроверки 1. Что понимается под последовательностью из n испытаний? 2. Напишите формулу Бернулли. При решении какого типа задач она применяется? 3. Что такое наивероятнейшее число наступления события? Как вычисляется это число? 4. Сформулируйте локальную теорему Лапласа. При каких условиях она применяется? 5. Напишите формулу Пуассона. При каких условиях она применяется? 6. Сформулируйте интегральную теорему Лапласа. 7. Напишите формулу для вычисления вероятности отклонения относительной частоты от вероятности появления события в независимых испытаниях.
Тема 12. Случайная величина и ее числовые характеристики Литература: (1), гл. VI, § 1-3, упр.1, гл. VII, § 1-3, упр. 1, гл. VIII, § 1-4, 7, упр.4, гл. XII,§ 2.5,7,8, гл. IV, § 1, 4 – 6., (4), ч. II, гл. III,§ 9-12, упр.1, 3, 4, 7, 9.
Понятие случайной величины - основное в теории вероятностей.
Случайной называют величину, которая в результате испытания примет одно и только одно возможное значение, наперед неизвестное и зависящее от случайных причин, которые заранее не могут быть учтены.
В этой теме рассматриваются два вида случайных величин: дискретные и непрерывные.
Дискретные – это величины, возможные значения которых представляют собой изолированные числа, то есть числа, отделенные промежутками не содержащими возможных значений.
Непрерывные – это величины, возможные значения которых сплошь заполняют некоторый промежуток.
Следует хорошо усвоить способы задания случайных величин дискретного и непрерывного типов. Обратите внимание на то, что интегральная функция служит для задания как непрерывной, так и дискретной случайной величины. Дифференциальная же функция применима лишь для величин непрерывных. Далее необходимо усвоить определение числовых характеристик случайных величин, уяснить их смысл (математическое ожидание характеризует среднее значение возможных значений случайной величины, а дисперсия и среднее квадратическое отклонение – рассеяние возможных значений вокруг математического ожидания). В эту тему входит изучение одного из важнейших распределений непрерывной случайной величины –нормального распределения. Широкое распространение нормального распределения объясняет теорема Ляпунова: закон распределения суммы достаточно большого числа независимых случайных величин с произвольными законами распределения близок к нормальному распределению. Необходимо научиться находить вероятность того, что нормально распределенная случайная величина примет значение, принадлежащее заданному интервалу и вероятность того, что отклонение нормально распределенной случайной величины от ее математического ожидания по абсолютной величине не будет превосходить заданного положительного числа. В заключение следует разобрать вопросы, относящиеся к закону больших чисел. Закон больших чисел выражается рядом теорем (Чебышева, Бернулли и др.), указывающих условия, при выполнении которых совокупное действие очень многих случайных причин приводит к результату, почти не зависящему от случая. Наибольшее внимание надо уделить теореме Чебышева и значению ее для практики. Это теорема обосновывает статистический метод оценки математического ожидания. Среднее арифметическое при большом числе испытаний можно принять за математическое ожидание случайной величины.
Задача 27. Задан закон распределения дискретной случайной величины:
Вычислить: 1) Математическое ожидание; 2) Дисперсию; 3) Среднее квадратическое отклонение. Решение. 1) Математическое ожидание дискретной случайной величины вычисляется по формуле: Подставляя данные задачи в эту формулу, получим:
2) Дисперсия дискретной случайной величины вычисляется по формуле:
Подставляя данные задачи в эту формулу, получим:
3) Среднее квадратическое отклонение дискретной случайной величины вычисляется по формуле:
Задача 28. Средняя длина листьев садовой земляники на некотором участке равна 7,4 см. Отдельные отклонения от этого значения случайные, распределены нормально со средним квадратическим отклонением 0.8 см. Наугад взят один лист. Найти вероятность того, что его длина: 1) будет в пределах от 7,0 см до 8,2 см; 2) отклонится от средней длины не более чем на 0,2 см.
|

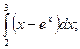 б)
б) 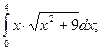 в)
в) 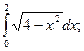
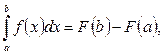 где F(x) – первообразная для функции f(x).
где F(x) – первообразная для функции f(x).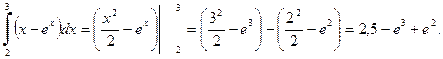
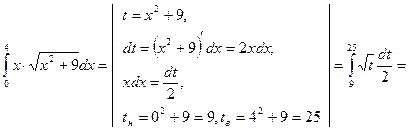
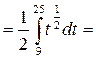
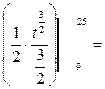


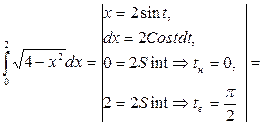


 и прямой
и прямой 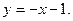
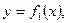 сверху кривой
сверху кривой 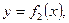 слева и справа соответственно прямыми x =a, х =в, вычисляется по формуле:
слева и справа соответственно прямыми x =a, х =в, вычисляется по формуле:  (***)
(***)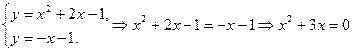
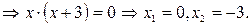

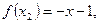
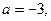
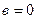 получим:
получим:

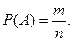

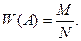
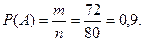
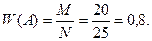
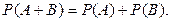
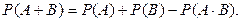
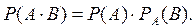
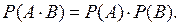
 образующих полную группу, равна сумме произведений вероятностей каждого из этих событий на соответствующую условную вероятность события А:
образующих полную группу, равна сумме произведений вероятностей каждого из этих событий на соответствующую условную вероятность события А: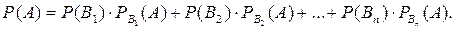
 т.к. число исходов, благоприятствующих событию А равно 120, а число всех исходов испытания n=1000.
т.к. число исходов, благоприятствующих событию А равно 120, а число всех исходов испытания n=1000. 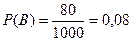 , т.к. число исходов, благоприятствующих событию В равно 80.
, т.к. число исходов, благоприятствующих событию В равно 80.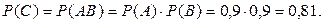
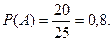

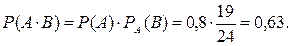
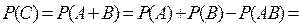
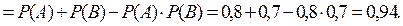
 где
где 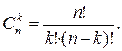
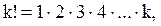
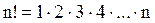
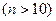 , то формула Бернулли требует громоздких вычислений, поэтому пользуются асимптотической формулой Лапласа:
, то формула Бернулли требует громоздких вычислений, поэтому пользуются асимптотической формулой Лапласа: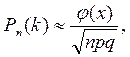 где
где 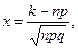
 -четная функция Лапласа, т.е.
-четная функция Лапласа, т.е. 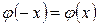 .
. , то используют формулу Пуассона:
, то используют формулу Пуассона: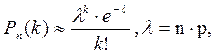
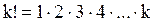
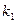 раз и не более
раз и не более 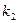 раз. Для определения этой вероятности служит интегральная теорема Лапласа:
раз. Для определения этой вероятности служит интегральная теорема Лапласа: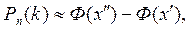 где
где 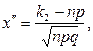
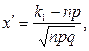

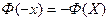 - нечетная функция Лапласа (см. приложение 2).
- нечетная функция Лапласа (см. приложение 2).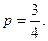 Посеяно 6 семян. Найти вероятность того, что будет:
Посеяно 6 семян. Найти вероятность того, что будет: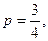 тогда
тогда 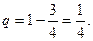
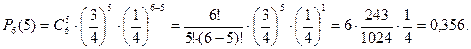
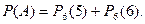
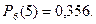
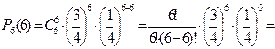
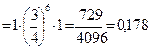
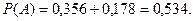
 , противоположным событию А, будет не более 1 всхода из 6 семян, т. е. или один всход, или ни одного.
, противоположным событию А, будет не более 1 всхода из 6 семян, т. е. или один всход, или ни одного.
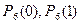 определяются по формуле Бернулли:
определяются по формуле Бернулли: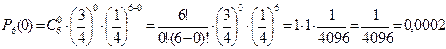
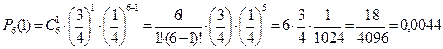
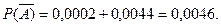


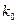 наступления события в независимых испытаниях определяется с помощью двойного неравенства
наступления события в независимых испытаниях определяется с помощью двойного неравенства 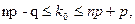 где
где
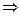
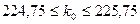

 вычисляется по локальной теореме Лапласа.
вычисляется по локальной теореме Лапласа.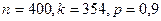 значит
значит 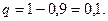

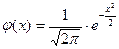 , найдем
, найдем 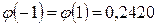
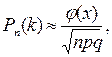 получим
получим 


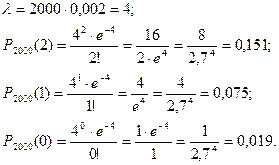
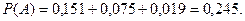
 раз и не более
раз и не более  раз вычисляется в силу интегральной теоремы Лапласа по приближенной формуле
раз вычисляется в силу интегральной теоремы Лапласа по приближенной формуле 

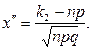
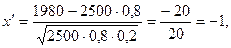
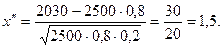
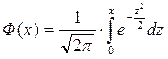 и, учитывая, что
и, учитывая, что 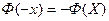 , получим
, получим