Показательный (экспоненциальный) закон распределения.Непрерывная случайная величина Х имеет показательный (экспоненциальный) закон распределения с параметром
Теорема. Функция распределения случайной величины Х, распределенной по показательному (экспоненциальному) закону распределения, есть Показательный закон распределения играет большую роль в теории массового обслуживания и теории надежности. Так, например, интервал времени Т между двумя соседними событиями в простейшем потоке имеет показательное распределение с параметром Показательный закон (и только он!) обладает важным свойством: Если промежуток времени Т, распределенный по показательному закону, уже длился некоторое время t, то это никак не влияет на закон распределения оставшейся части Т1 = Т – t промежутка, т.е. закон распределения Т1 остается таким же, как и всего промежутка Т.
Нормальный закон распределения наиболее часто встречается на практике. Главная особенность, выделяющая его среди других законов, состоит в том, что он является предельным законом, к которому приближаются другие законы распределения при весьма часто встречающихся типичных условиях. Непрерывная случайная величины Х имеет нормальный закон распределения (закон Гаусса) с параметрами а и Кривую нормального распределения называют нормальной, или гауссовой кривой. На рисунке приведены нормальная кривая и график функции распределения случайной величины Х, имеющей нормальный закон. Нормальная кривая симметрична относительно прямой х = а, имеет максимум в точке х = а, равный
Теорема. Математическое ожидание случайной величины Х, распределенной по нормальному закону, равно параметру а этого закона, т.е. М(Х) = а, а ее дисперсия – параметру Выясним, как будет меняться нормальная кривая при изменении параметров а и Нормальный закон распределения случайной величины с параметрами а = 0,
Геометрически функция распределения представляет собой площадь под нормальной кривой на интервале Свойства случайной величины, распределенной по нормальному закону: 10. Вероятность попадания случайной величины Х, распределенной по нормальному закону, в интервал [х1, х2], равна 20. Вероятность того, что отклонение случайной величины Х, распределенной по нормальному закону, от математического ожидания а не превысит величину Вычислим по формуле (63) вероятности При При При «Правило трех сигм»: Если случайная величина Х имеет нормальный закон распределения с параметрами а и Коэффициент асимметрии нормального распределения А = 0. Эксцесс нормального распределения равен нулю.
8. Логарифмически – нормальное распределение. Непрерывная случайная величина Х имеет логарифмически – нормальное (логнормальное) распределение, если ее логарифм подчинен нормальному закону. Так как при x> 0 неравенства X<x и lnX < ln x равносильны, то функция распределения логнормального распределения совпадает с функцией нормального распределения для случайной величины lnX, т.е.
Дифференцируя (64) по х, получим выражение плотности вероятности для логнормального распределения Логнормальное распределение широко используется для описания распределения доходов, банковских вкладов, цен активов, месячной заработной платы, посевных площадей под разные культуры, долговечности изделий в режиме износа и старения и др.
9. Распределение Хи – квадрат. Распределением Плотность вероятности где
|

 , если ее плотность вероятности имеет вид:
, если ее плотность вероятности имеет вид:  (57)
(57) Кривая распределения
Кривая распределения 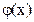 и график функции распределения F(x) случайной величины Х приведены на рисунке.
и график функции распределения F(x) случайной величины Х приведены на рисунке. ее математическое ожидание
ее математическое ожидание  , (т.е. ее среднему квадратическому отклонению
, (т.е. ее среднему квадратическому отклонению  ), а дисперсия
), а дисперсия  (58)
(58) - интенсивностью потока.
- интенсивностью потока. 7. Нормальный закон распределения.
7. Нормальный закон распределения. , если ее плотность вероятности имеет вид:
, если ее плотность вероятности имеет вид:  (59)
(59) , т.е.
, т.е. , и две точки перегиба
, и две точки перегиба  с ординатой
с ординатой  . В выражении плотности нормального распределения параметры обозначены буквами а и
. В выражении плотности нормального распределения параметры обозначены буквами а и  , и меняется параметр а, т.е. центр симметрии распределения, то нормальная кривая будет смещаться вдоль оси абсцисс, не меняя формы (см. рис.). Если а = const и меняется параметр
, и меняется параметр а, т.е. центр симметрии распределения, то нормальная кривая будет смещаться вдоль оси абсцисс, не меняя формы (см. рис.). Если а = const и меняется параметр  ), то меняется ордината точки максимума кривой. При увеличении
), то меняется ордината точки максимума кривой. При увеличении 

 Теорема. Функция распределения случайной величины Х, распределенной по нормальному закону, выражается через функцию Лапласа Ф(х) по формуле:
Теорема. Функция распределения случайной величины Х, распределенной по нормальному закону, выражается через функцию Лапласа Ф(х) по формуле: (61)
(61) (см. рис.). Как видим, она состоит из двух частей: первой, на интервале
(см. рис.). Как видим, она состоит из двух частей: первой, на интервале  , равной
, равной 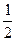 , т.е. половине всей площади под нормальной кривой, и второй, на интервале (а, х), равной
, т.е. половине всей площади под нормальной кривой, и второй, на интервале (а, х), равной  .
. , где
, где  (62)
(62) (по абсолютной величине), равна
(по абсолютной величине), равна  , где
, где  (63)
(63) при различных значениях
при различных значениях  , используя значения функции Лапласа:
, используя значения функции Лапласа:
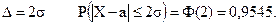

 . Нарушение «правила трех сигм», т.е. отклонение нормально распределенной случайной величины Х больше, чем на 3
. Нарушение «правила трех сигм», т.е. отклонение нормально распределенной случайной величины Х больше, чем на 3 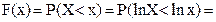
 . (64)
. (64)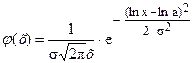 (65) Математическое ожидание случайной величины, распределенной по логнормальному закону, имеет вид:
(65) Математическое ожидание случайной величины, распределенной по логнормальному закону, имеет вид:  , дисперсия:
, дисперсия:  , мода
, мода  , медиана Ме (Х) = а. Очевидно, что чем меньше
, медиана Ме (Х) = а. Очевидно, что чем меньше  (хи – квадрат) с k степенями свободы называется распределение суммы квадратов k независимых случайных величин, распределенных по стандартному нормальному закону, т.е.
(хи – квадрат) с k степенями свободы называется распределение суммы квадратов k независимых случайных величин, распределенных по стандартному нормальному закону, т.е.  (66) где Zi (I = 1, 2, …, k) имеет нормальное распределение N(0; 1).
(66) где Zi (I = 1, 2, …, k) имеет нормальное распределение N(0; 1).
 – гамма - функция Эйлера (для целых положительных значений Г(у) = (у – 1)!). При k>30 распределение случайной величины Z близко к нормальному закону.
– гамма - функция Эйлера (для целых положительных значений Г(у) = (у – 1)!). При k>30 распределение случайной величины Z близко к нормальному закону.


