РАЗВЕТВЛЯЮЩИЙСЯ ВЫЧИСЛИТЕЛЬНЫЙ ПРОЦЕСС. В заданиях 1 - 13 требуется составить формулу, которая соответствует графику функции f(X)
В заданиях 1 - 13 требуется составить формулу, которая соответствует графику функции f(X). На основании этой формулы разработать алгоритм и программу, которая по введенному значению Х вычисляет и выводит на экран монитора значение Y = f(X). Привести столько исходных данных и результатов расчетов (прогонов программы), чтобы проверить работоспособность всех ветвей алгоритма.
В заданиях 14 - 20 требуется найти кратчайшее расстояние от произвольной точки M(X,Y) с координатами X и Yдо контура фигуры, точка может располагаться как внутри так и вне геометрической фигуры. Необходимо рассмотреть все возможные варианты и составить для них формулы. На основании этих формул разработать алгоритм и программу, которая по введенным с клавиатуры значениям Х и Y вычисляет расстояние и выводит результат на экран монитора.
21. а) б) координаты исследуемой
22. а) б) координаты исследуемой
23. а) б) координаты исследуемой точки: (0.2; 0.9).
б) координаты исследуемой
25. а)
26. а) б) координаты исследуемой
27. а) б) координаты исследуемой
28. а) б) координаты исследуемой
29. а) б) координаты исследуемой
б) координаты исследуемой
РАЗВЕТВЛЯЮЩИЙСЯ ВЫЧИСЛИТЕЛЬНЫЙ ПРОЦЕСС Разветвляющимся называется такой вычислительный процесс, в котором, в зависимости от выполнения некоторого условия, вычисления происходят по одной из нескольких заранее предусмотренных ветвей. Разветвление процесса обозначается в блок-схемах алгоритма условным блоком. Пример: По введенному значению
Формализуем условие задачи. Дано: Найти: Приведем таблицу имен объектов решаемой задачи.
Блок схема алгоритма решения задачи приведена на рис. 2.3. В разветвляющихся вычислительных процессах трассировку необходимо выполнять для каждой из возможных ветвей блок-схемы. Блок-схема рассмотренного примера содержит три ветви: · Для · для · для Для каждой ветви нужно подобрать соответствующее значение исходных данных и заполнить таблицу трассировки.
Рис. 2.3 Блок-схема разветвляющегося вычислительного процесса Таблица трассировки для
Таблица трассировки для
Таблица трассировки для
Поясним процесс программирования разветвляющегося вычислительного процесса. Блоку начала ставим в соответствие предложение PROGRAM – заголовок программы. Блоку описания – рубрику VAR декларативной части для описания используемых величин. Далее следует описания действия, объединенные в составной оператор, заключенный в операторные скобки BEGIN¼END и представляющий собой исполняемую часть. Блоку ввода ставим в соответствие оператор вызова процедуры вывода информации на экран дисплея WRITELN для вывода приглашения ко вводу и вызов процедуры ввода информации от клавиатуры READLN для ввода значения PROGRAM RAZV; VAR X,Y:REAL; BEGIN WRITELN('ВВЕДИ X'); READLN(X); IF X<=-1 THEN Y:=-1 ELSE IF X<=1 THEN Y:=X ELSE Y:=1; WRITELN('Y=', Y:10:4); END. Для программирования задач этого раздела необходимо использовать операторы IF … THEN … ELSE или CASE … OF. Оператор GOTO использовать запрещается! Для всех заданий этого раздела следует разработать алгоритм и программу.
|










 В заданиях 21 – 30 требуется при заданном значении x вычислить y(x), а также проверить принадлежность точки с координатами (x1, y1) заштрихованной области. Значения x, x1, y1 ввести с клавиатуры. Результаты вывести на экран монитора.
В заданиях 21 – 30 требуется при заданном значении x вычислить y(x), а также проверить принадлежность точки с координатами (x1, y1) заштрихованной области. Значения x, x1, y1 ввести с клавиатуры. Результаты вывести на экран монитора. при x = 4.741;
при x = 4.741;
 при x=2.312;
при x=2.312;
 при
при  24. а)
24. а) 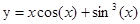 при x=32.872;
при x=32.872; при x = -2.6312;
при x = -2.6312; б) координаты исследуемой
б) координаты исследуемой
 при x=-0.387;
при x=-0.387;
 при x=4.352;
при x=4.352;
 при x=0.112;
при x=0.112;
 при x=-0.7129;
при x=-0.7129; 30. а)
30. а)  при x=-1.5;
при x=-1.5;
 вывести значение релейной функции
вывести значение релейной функции  , где
, где
 – значение релейной функции.
– значение релейной функции.

 выполняются блоки 1, 2, 6, 5, 8
выполняются блоки 1, 2, 6, 5, 8 выполняются блоки 1, 2, 3, 7, 5, 8
выполняются блоки 1, 2, 3, 7, 5, 8 выполняются блоки 1, 2, 3, 4, 5, 8
выполняются блоки 1, 2, 3, 4, 5, 8

 ,
,  .
.
 , да
, да

 ;
;  .
.
 , нет
, нет
 , нет
, нет

 ,
,  .
.
 , нет
, нет
 , нет
, нет




