Рассмотрим несколько простых случаев.1. Разность фаз равна нулю или четному числу π, то есть
так как
Рис. 2.3 2. Разность фаз равна нечетному числу π, то есть
На рис. 2.4 изображена амплитуда результирующего колебания А, равная разности амплитуд складываемых колебаний (колебания в противофазе).
Рис. 2.4 3. Разность фаз изменяется во времени произвольным образом:
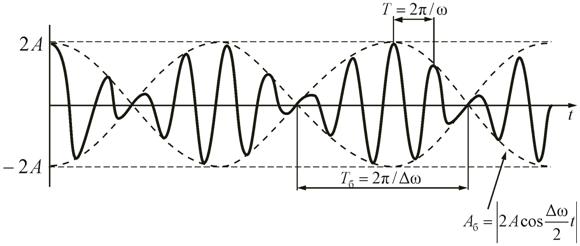
Из уравнения (2.2.6) следует, что Периодические изменения амплитуды колебания, возникающие при сложении двух гармонических колебаний с близкими частотами, называются биениями. Строго говоря, это уже не гармонические колебания. Пусть амплитуды складываемых колебаний равны А, а частоты равны ω и
Сложим эти выражения, пренебрегая
Результирующее колебание (2.2.7) можно рассматривать как гармоническое с частотой ω и амплитудой А б, которая изменяется по следующему периодическому закону:
Характер зависимости (2.2.8) показан на рис. 2.5, где сплошные жирные линии дают график результирующего колебания, а огибающие их – график медленно меняющейся по уравнению (2.2.7) амплитуды.
Рис. 2.5 Определение частоты тона (звука определенной высоты) биений между эталонным и измеряемым колебаниями – наиболее широко применяемый на практике метод сравнения измеряемой величины с эталонной. Метод биений используется для настройки музыкальных инструментов, анализа слуха и т.д. Вообще, колебания вида Любые сложные периодические колебания
Представление периодической функции в таком виде связывают с понятием гармонического анализа сложного периодического колебания, или разложения Фурье (то есть представление сложных модулированных колебаний в виде ряда (суммы) простых гармонических колебаний). Слагаемые ряда Фурье, определяющие гармонические колебания с частотами ω, 2ω, 3ω,..., называются первой (или основной), второй, третьей и т.д. гармониками сложного периодического колебания. | ||||||||||||||||||||
| Сложение взаимно перпендикулярных колебаний | ||||||||||||||||||||
Пусть некоторое тело колеблется и вдоль оси x, и вдоль оси y, т.е. участвует в двух взаимноперпендикулярных колебаниях:
Найдем уравнение результирующего колебания. Для простоты примем Разность фаз между обоими колебаниями равна: Чтобы получить уравнение траектории, надо исключить из этих уравнений время t. Упростим выражения, выбрав начало отсчета так, чтобы
Распишем второе уравнение через косинус суммы:
Отсюда Возведем обе части в квадрат:
Окончательное уравнение:
В результате мы получили уравнение эллипса, оси которого ориентированы относительно x и y произвольно (рис. 2.6).
Рис. 2.6 | ||||||||
| Фигуры Лиссажу | ||||||||
Рассмотрим некоторые частные случаи решений уравнения (2.3.2). 1. Начальные фазы колебаний одинаковы:
Тогда уравнение (2.3.2) примет вид:
отсюда получим уравнение результирующего колебания:
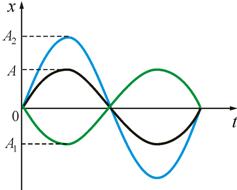
Это уравнение прямой, проходящей через начало координат (рис. 2.7, а). Следовательно, в результате сложения двух взаимно перпендикулярных колебаний с одинаковыми начальными фазами будут происходить колебания вдоль прямой, проходящей через начало координат.
Такие колебания называются линейно поляризованными. 2. Начальная разность фаз равна π. Тогда
Уравнение колебания в этом случае
То есть точка тоже будет колебаться вдоль прямой, проходящей через начало координат, но прямая лежит в других четвертях по сравнению с первым случаем (рис. 2.7, б). Амплитуда результирующего колебания в обоих случаях равна:
3. Начальная разность фаз равна π/2. Проанализируем уравнение (2.3.2), учитывая, что
Это уравнение эллипса с полуосями А 1 и А 2 (рис. 2.7, в). Случай эллиптически поляризованных колебаний. При 4. Все остальные разности фаз дают эллипсы с различным углом наклона относительно осей координат. Необходимо отметить, что все рассматриваемые случаи, все кривые – это эллипсы (даже прямая – частный случай эллипса). Фигуры, получаемые при сложении взаимно перпендикулярных колебаний разных частот, называются фигурами Лиссажу (Ж. Лиссажу (1822–1880) – французский физик). В простейших случаях можно сравнить частоты по виду фигур. В приведенных выше примерах рассматривались простейшие случаи, когда Таблица 1
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Свободные затухающие механические колебания | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Все реальные колебания являются затухающими. Энергия механических колебаний постепенно расходуется на работу против сил трения и амплитуда колебаний постепенно уменьшается (затухает).
 Во многих случаях в первом приближении можно считать, что при небольших скоростях силы, вызывающие затухание колебаний, пропорциональны величине скорости (например маятник). Тогда сила трения (или сопротивления)
Во многих случаях в первом приближении можно считать, что при небольших скоростях силы, вызывающие затухание колебаний, пропорциональны величине скорости (например маятник). Тогда сила трения (или сопротивления)
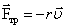 ,
где r – коэффициент сопротивления, ,
где r – коэффициент сопротивления,  – скорость движения.
Запишем второй закон Ньютона для затухающих прямолинейных колебаний вдоль оси x: – скорость движения.
Запишем второй закон Ньютона для затухающих прямолинейных колебаний вдоль оси x:
 ,
где kx – возвращающая сила, r υ x – сила трения. Это уравнение можно переписать: ,
где kx – возвращающая сила, r υ x – сила трения. Это уравнение можно переписать:
 , отсюда следует: , отсюда следует: 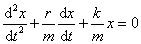 .
Введем обозначения: .
Введем обозначения: 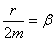 ; ;  .
Тогда однородное дифференциальное уравнение второго порядка, описывающее затухающее колебательное движение, запишем так: .
Тогда однородное дифференциальное уравнение второго порядка, описывающее затухающее колебательное движение, запишем так:
Решение уравнения (3.1.1) имеет вид (при
Здесь А 0 и φ0 определяются из краевых условий задачи (начальных и граничных), а β и ω – из самого уравнения. Найдем круговую частоту ω. Здесь она уже не равна Для этого найдем первую и вторую производные от x:
Подставим эти значения в (3.1.1) и сократим на
Сократим на
где ω0 – круговая частота собственных колебаний (без затухания); ω – круговая частота свободных затухающих колебаний. Из этого выражения ясно, почему решение (3.1.1) будет только при Для колебаний под действием различных сил (квазиупругих) значения ω, β, ω0 будут различными. Например, для колебаний под действием упругой силы
Затухающие колебания представляют собой непериодические колебания, так как в них не повторяется, например, максимальное значение амплитуды. Поэтому называть ω – циклической (повторяющейся, круговой) частотой можно лишь условно. По этой же причине и
называется условным периодом затухающих колебаний. | ||||||||
| Коэффициент затухания и логарифмический декремент затухания | ||||||||
Найдем отношение значений амплитуды затухающих колебаний в моменты времени t и  (рис. 3.1): (рис. 3.1):
 ,
где β – коэффициент затухания. ,
где β – коэффициент затухания.
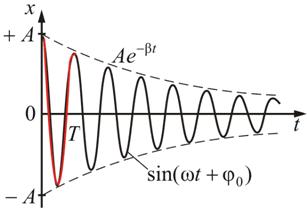 Рис. 3.1
Натуральный логарифм отношения амплитуд, следующих друг за другом через период Т, называется логарифмическим декрементом затухания χ:
Рис. 3.1
Натуральный логарифм отношения амплитуд, следующих друг за другом через период Т, называется логарифмическим декрементом затухания χ:
 ; ;
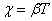 .
Выясним физический смысл χиβ.
Время релаксации τ – время, в течение которого амплитуда А уменьшается в e раз. .
Выясним физический смысл χиβ.
Время релаксации τ – время, в течение которого амплитуда А уменьшается в e раз.
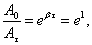 отсюда отсюда 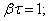  Следовательно, коэффициент затухания β есть физическая величина, обратная времени, в течение которого амплитуда уменьшается в е раз.
Пусть N число колебаний, после которых амплитуда уменьшается в e раз. Тогда
Следовательно, коэффициент затухания β есть физическая величина, обратная времени, в течение которого амплитуда уменьшается в е раз.
Пусть N число колебаний, после которых амплитуда уменьшается в e раз. Тогда
 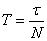 ; ; 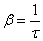 ; ;
 .
Следовательно, логарифмический декремент затухания χ есть физическая величина, обратная числу колебаний, по истечении которых амплитуда А уменьшается в e раз.
Если χ = 0,01, то N = 100.
При большом коэффициенте затухания происходит не только быстрое уменьшение амплитуды, но и заметно увеличивается период колебаний. Когда сопротивление становится равным критическому .
Следовательно, логарифмический декремент затухания χ есть физическая величина, обратная числу колебаний, по истечении которых амплитуда А уменьшается в e раз.
Если χ = 0,01, то N = 100.
При большом коэффициенте затухания происходит не только быстрое уменьшение амплитуды, но и заметно увеличивается период колебаний. Когда сопротивление становится равным критическому 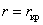 , а , а 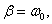 то круговая частота обращается в нуль ( то круговая частота обращается в нуль ( ), а ( ), а (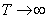 ), колебания прекращаются. Такой процесс называется апериодическим (рис. 3.2). ), колебания прекращаются. Такой процесс называется апериодическим (рис. 3.2).
 Рис. 3.2
Отличия в следующем. При колебаниях тело, возвращающееся в положение равновесия, имеет запас кинетической энергии. В случае апериодического движения энергия тела при возвращении в положение равновесия оказывается израсходованной на преодоление сил сопротивления, трения.
Рис. 3.2
Отличия в следующем. При колебаниях тело, возвращающееся в положение равновесия, имеет запас кинетической энергии. В случае апериодического движения энергия тела при возвращении в положение равновесия оказывается израсходованной на преодоление сил сопротивления, трения.
| |||
| Вынужденные механические колебания | |||
Рассмотрим систему, на которую, кроме упругой силы (– kx) и сил сопротивления (– r υ), действует добавочная периодическая сила F – вынуждающая сила. Для колебаний вдоль оси x запишем:
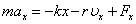 – основное уравнение колебательного процесса, или
– основное уравнение колебательного процесса, или
где fx = Fx / m – вынуждающая сила, изменяющаяся по гармоническому закону:
Через некоторое время после начала действия вынуждающей силы колебания системы будут совершаться с частотой вынуждающей силы ω.
Уравнение установившихся вынужденных колебаний:
Наша задача найти амплитуду А и разность фаз φ между смещением вынужденных колебаний и вынуждающей силой. Обратим внимание на то, что скорость на π/2 опережает смещение, а ускорение на π/2 опережает скорость (см. п. 1.3). Из (3.3.2) получим:
Преобразуем и (3.3.2) через косинус:
Обозначим Подставим (3.3.3), (3.3.4) и (3.3.5) в (3.3.1):
Каждое слагаемое последнего уравнения можно представить в виде соответствующего вращающегося вектора амплитуды:
Вектор амплитуды силы найдем по правилу сложения векторов:
Рис. 3.3 Из рис. 3.2 видно, что
Таким образом, При постоянных F 0, m и β амплитуда зависит только от соотношения круговых частот вынуждающей силы ω и свободных незатухающих колебаний системы ω0. Начальную фазу вынужденных колебаний можно найти из выражения
Из рис. 3.3 видно, что сила опережает смещение на угол, который определяется из выражения
Проанализируем выражение (3.3.7). 1)
– статическая амплитуда (колебания не совершаются). 2)
Рис. 3.4 3)
4ω ≠ 0, следовательно, выражение в скобках равно нулю:
где ωрез – резонансная частота. Явление возрастания амплитуды вынужденных колебаний при приближении частоты вынуждающей силы к ωрез называется резонансом. Для консервативной системы, т.е. С увеличением коэффициента затухания β явление резонанса проявляется все слабее и исчезает при | ||||||||||||||||||||||||||||||||
| Автоколебания | ||||||||||||||||||||||||||||||||
Наблюдая колебания листьев деревьев, дорожных знаков над проезжей частью улиц, полотнищ на ветру и др., мы понимаем, что во всех перечисленных случаях незатухающие колебания происходят за счет энергии постоянно дующего ветра. При этом сама колебательная система производит отбор энергии ветра в нужный момент времени и в количестве, требуемом для компенсации неизбежно присутствующих энергетических потерь. Колебания в этих системах начинаются самопроизвольно за счет начальных флуктуаций (дрожаний) колеблющихся предметов. Частота и амплитуда установившихся колебаний определяется как параметрами самой системы, так и параметрами ее взаимодействия с ветром. Такие колебания являются примерами автоколебаний, а сами системы – примерами автоколебательных систем.
Классическим примером автоколебательной системы служат механические часы с маятником и гирями. Эти часы периодически «черпают» энергию при опускании гирь, подвешенных к цепочке, перекинутой через шестерню часового механизма.
Принцип работы всех автоколебательных систем можно понять, обратившись к схеме, изображенной на рис. 3.5.
 Рис. 3.5
Периодическим поступлением энергии в колебательную систему от источника энергии по каналу АВ управляет сама колебательная система посредством обратной связи. Схематически это изображено в виде некоторого запирающего канал АВ устройства (ключа), который управляется самой системой. Так, в зависимости от положения и скорости колеблющегося листа на ветру будет различной мощность сил аэродинамического давления.
В конструкции часового механизма (рис. 3.6) присутствует специальное устройство – анкер, выполняющий роль ключа. Этот анкер, представляющий собой коромысло, приводится в колебание самим маятником часов. При определенных положениях он «отпирает» одну из шестерен часового механизма. В этот момент времени шестерня проворачивается за счет момента сил, приложенного со стороны натянутой цепи с грузом. Груз при этом опускается на небольшую величину. Количество энергии, поступающей в часовой механизм, равно по величине уменьшению потенциальной энергии груза в поле силы тяжести.
Рис. 3.5
Периодическим поступлением энергии в колебательную систему от источника энергии по каналу АВ управляет сама колебательная система посредством обратной связи. Схематически это изображено в виде некоторого запирающего канал АВ устройства (ключа), который управляется самой системой. Так, в зависимости от положения и скорости колеблющегося листа на ветру будет различной мощность сил аэродинамического давления.
В конструкции часового механизма (рис. 3.6) присутствует специальное устройство – анкер, выполняющий роль ключа. Этот анкер, представляющий собой коромысло, приводится в колебание самим маятником часов. При определенных положениях он «отпирает» одну из шестерен часового механизма. В этот момент времени шестерня проворачивается за счет момента сил, приложенного со стороны натянутой цепи с грузом. Груз при этом опускается на небольшую величину. Количество энергии, поступающей в часовой механизм, равно по величине уменьшению потенциальной энергии груза в поле силы тяжести.
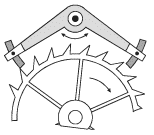 Рис. 3.6
Важно отметить, что любая автоколебательная система нелинейна. На схеме это отражено наличием в системе обратной связи нелинейного ограничителя сигнала, управляющего ключом. Нелинейность системы проявляется в том, что при начальном нарастании амплитуды колебаний, порожденных флуктуациями, поступление энергии в систему за каждый последующий период колебаний увеличивается нелинейно, т.е. прирост поступающей энергии становится все меньше и меньше. Естественно, что амплитуда колебаний достигнет такой установившейся величины, при которой приток энергии и ее потери будут равны.
Рис. 3.6
Важно отметить, что любая автоколебательная система нелинейна. На схеме это отражено наличием в системе обратной связи нелинейного ограничителя сигнала, управляющего ключом. Нелинейность системы проявляется в том, что при начальном нарастании амплитуды колебаний, порожденных флуктуациями, поступление энергии в систему за каждый последующий период колебаний увеличивается нелинейно, т.е. прирост поступающей энергии становится все меньше и меньше. Естественно, что амплитуда колебаний достигнет такой установившейся величины, при которой приток энергии и ее потери будут равны.
|

 , где
, где  . Тогда
. Тогда 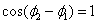 и
и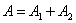 ,
,
 , т.е. амплитуда результирующего колебания А равна сумме амплитуд складываемых колебаний (колебания синфазны) (рис. 2.3).
, т.е. амплитуда результирующего колебания А равна сумме амплитуд складываемых колебаний (колебания синфазны) (рис. 2.3).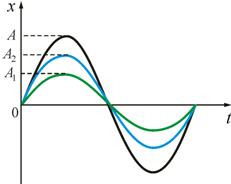
 , где
, где 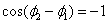 . Отсюда
. Отсюда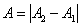 .
.

 и будет изменяться в соответствии с величиной
и будет изменяться в соответствии с величиной  . Поэтому при сложении некогерентных колебаний не имеет смысла говорить о сложении амплитуд, но в некоторых случаях наблюдаются вполне определенные закономерности. Для практики особый интерес представляет случай, когда два складываемых колебания одинакового направления мало отличаются по частоте. В результате сложения этих колебаний получаются колебания с периодически изменяющейся амплитудой.
. Поэтому при сложении некогерентных колебаний не имеет смысла говорить о сложении амплитуд, но в некоторых случаях наблюдаются вполне определенные закономерности. Для практики особый интерес представляет случай, когда два складываемых колебания одинакового направления мало отличаются по частоте. В результате сложения этих колебаний получаются колебания с периодически изменяющейся амплитудой. , причем
, причем  . Начало отсчета выбираем так, чтобы начальные фазы обоих колебаний были равны нулю:
. Начало отсчета выбираем так, чтобы начальные фазы обоих колебаний были равны нулю:

 , так как
, так как  .
.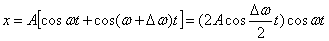 .
.
 ;
;
 .
.
 называются модулированными. Частные случаи: амплитудная модуляция и модулирование по фазе или частоте. Биение – простейший вид модулированных колебаний.
называются модулированными. Частные случаи: амплитудная модуляция и модулирование по фазе или частоте. Биение – простейший вид модулированных колебаний. можно представить в виде суперпозиции одновременно совершающихся гармонических колебаний с различными амплитудами, начальными фазами, а также частотами, кратными циклической частоте ω:
можно представить в виде суперпозиции одновременно совершающихся гармонических колебаний с различными амплитудами, начальными фазами, а также частотами, кратными циклической частоте ω: .
. ;
; 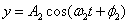 .
.
 .
.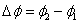 .
. , т.е.
, т.е.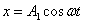 ;
;  .
. или
или  .
.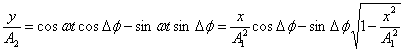 .
. .
. ;
;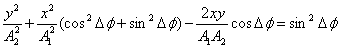 .
.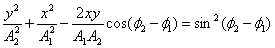 .
.


 т.е.
т.е. 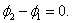
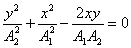 или
или 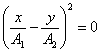 ;
;

 ,следовательно
,следовательно ;
;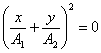 .
.
 .
.
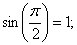
 .
.
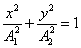 .
.
 получим уравнение окружности (циркулярно-поляризованные колебания).
получим уравнение окружности (циркулярно-поляризованные колебания). Если
Если  , то в результате будут получаться уже не эллипсы, а более сложные фигуры Лиссажу. В табл. 1 приведены несколько фигур Лиссажу для разных соотношений частот колебаний и заданной разности фаз.
, то в результате будут получаться уже не эллипсы, а более сложные фигуры Лиссажу. В табл. 1 приведены несколько фигур Лиссажу для разных соотношений частот колебаний и заданной разности фаз.



















 .
.
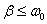 ):
):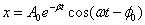 .
.
 .
. ,
,
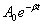 :
:
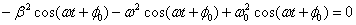 .
. и выразим ω:
и выразим ω: ,
, ,
, ;
;  ;
; 
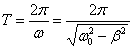
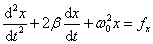 ,
,
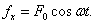
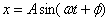 .
.
 ,
,
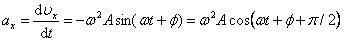 .
.
 .
.
 – угол между смещением и вынуждающей силой.
– угол между смещением и вынуждающей силой.
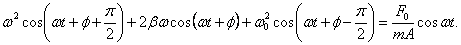
 – амплитуда ускорения;
– амплитуда ускорения; 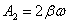 – а мплитуда скорости;
– а мплитуда скорости;  – амплитуда смещения;
– амплитуда смещения; 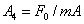 – амплитуда вынуждающей силы, причем
– амплитуда вынуждающей силы, причем 
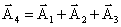 .
.
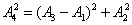 . Найдем амплитуду А:
. Найдем амплитуду А:
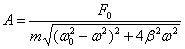 .
.
 и
и 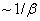 .
.
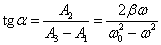 .
.
 (затухания нет). С увеличением ω (но при
(затухания нет). С увеличением ω (но при 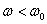 ) амплитуда растет и при
) амплитуда растет и при  резко возрастает (
резко возрастает ( ). Это явление называется резонанс. При дальнейшем увеличении ω (
). Это явление называется резонанс. При дальнейшем увеличении ω (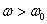 ) амплитуда опять уменьшается (рис. 3.4).
) амплитуда опять уменьшается (рис. 3.4).
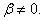 Амплитуда будет максимальна при минимальном значении знаменателя. Для нахождения точки перегиба возьмем первую производную по ω от подкоренного выражения (3.3.7) и приравняем ее к нулю:
Амплитуда будет максимальна при минимальном значении знаменателя. Для нахождения точки перегиба возьмем первую производную по ω от подкоренного выражения (3.3.7) и приравняем ее к нулю:
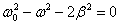 , отсюда
, отсюда ,
,
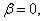 из (3.3.9) следует
из (3.3.9) следует  ; для диссипативной ωрез несколько меньше собственной круговой частоты ω0 (рис. 3.4).
; для диссипативной ωрез несколько меньше собственной круговой частоты ω0 (рис. 3.4). .
.


