С малой поверхностью и точечных испарителей
Для анализа распределения пленки по толщине используют, как правило, идеальную модель испарения и конденсации, которая предусматривает выполнение законов Ламберта-Кнудсена и формулы Лэнгмюра (2.1) для скоростей испарения, а также полную конденсацию паров испаренного вещества на подложке (коэффициент конденсации равен 1 независимо от материала подложки и интенсивности испаренного вещества). Процесс испарения происходит с зеркальной поверхности расплава. Распределение испаренного вещества описывается уравнениями (2.3) и (2.4), в зависимости от угла падения и расстояния от испарителя до подложки. Следовательно, профиль толщины пленки может быть выведен для любой формы площади подложки и любого положения подложки относительно испарителя. Однако обычно используют плоские подложки и располагают их параллельно эффективной плоскости испарения. Для того чтобы перейти от массы к толщине пленки, выделим малое количество вещества с массой dMr, которое занимает объем dArdпл. толщину пленки запишем в виде
где ρ – плотность материала подложки. Для плоскопараллельной подложки, отстоящей от испарителя на расстоянии h, угол падения θ равен углу испарения φ и cos θ = cos φ = h/r. Схематически система испаритель – подложка представлена на рис.2.3. Расстояние r от испарителя до элемента подложки dAr при данном h меняется с расстоянием l от центра подложки до элемента dAr по закону r2 = l2 + h2. если эти соотношения подставить в (2.3) и 2.4), то будем иметь: для испарителя с малой площадью
для точечного испарителя
Оба типа испарителя можно охарактеризовать с помощью величины отношения d/do, где do – толщина в центре подложки при l = 0 (рис.2.3.).
Тогда для испарителя с малой площадью
для точечного испарителя
2.4. Распределение пленки по толщине для кольцевого и дискового испарителей. На практике испарение осуществляют из испарителей, поверхность которых не является бесконечно малой. При использовании испарителей конечных размеров распределение пленок по толщине можно определить суммированием в данной точке по толщине вещества, испаренного из всех элементов dAe испарителя. При этом предполагается, что испарение происходит из всех точек испарителя с одной и той же скоростью.
Рассмотрим модель испарителя в виде круглого диска радиуса s поверхность испарения, которого параллельна плоской поверхности подложки. Следовательно, распределение испаренного вещества по подложке должно быть центрально-симметричным и описываться одной переменной, а именно, расстоянием от центра l. Схематично изображение системы испаритель - подложка приведено на рис.2.4. Дифференциальный элемент поверхности тонкого кольца можно представить в виде
Тройной интеграл возникает вследствие того, что необходимо рассмотреть полную испаренную массу Ме со всех элементов поверхности и их временную зависимость. После замены расстояния r на величины, характеризующие положение данной точки подложки относительно испарителя,
Отсюда легко получить окончательное выражение для d в случае бесконечно тонкого кольца, поскольку Таким образом, уравнение (2.11) для тонкого кольцевого испарителя принимает вид:
Однородность по толщине покрытия, получаемого от такого тонкого кольцевого испарителя, легко описать, используя толщину в центре подложки (при l = 0):
В этом случае параметром, характеризующим однородность по толщине, будет отношение d/d0. Помимо относительного расстояния от центра l/h уравнения (2.12) и (2.13) содержат также второй параметр - относительный радиус испарителя s/h. Рассмотрим теперь случай круглого дискового испарителя. Уравнение (2.11) следует проинтегрировать по величине радиуса диска s. После интегрирования по частям имеем
В этом случае полная масса испаренного вещества может быть представлена в виде
и
Следует отметить, что распределение по толщине, полученное от дискового или кольцевого испарителя, диаметр или ширина которых, конечны, но малы по сравнению с расстоянием испаритель - подложка, адекватно описываются формулами для источника с одним элементом поверхности и тонкого кольца. Преимущества испарителей с большой поверхностью заключается в первую очередь в том, что они при необходимых для испарения температурах имеют большую скорость испарения в соответствии с низким давлением паров. Следовательно, в таких испарителях вероятность химического взаимодействия между испаряемым веществом и материалом испарителя уменьшается.
|

 , (2.5)
, (2.5) , (2.6)
, (2.6) . (2.7)
. (2.7)
 , (2.8)
, (2.8) . (2.9)
. (2.9)
 , где α - угол между l и проекцией s на плоскость испарителя, то
, где α - угол между l и проекцией s на плоскость испарителя, то  . Подстановка этого соотношения, а также уравнения (2.5) в выражение (2.3) для испарителя с малой поверхностью приводит к следующему выражению для распределения по толщине от дискового испарителя
. Подстановка этого соотношения, а также уравнения (2.5) в выражение (2.3) для испарителя с малой поверхностью приводит к следующему выражению для распределения по толщине от дискового испарителя . (2.10)
. (2.10)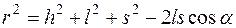 , может быть проведено интегрирование по α до 2π. После интегрирования имеем
, может быть проведено интегрирование по α до 2π. После интегрирования имеем . (2.11)
. (2.11) представляет собой полную массу испаренного вещества.
представляет собой полную массу испаренного вещества. . (2.12)
. (2.12) . (2.13)
. (2.13) . (2.14)
. (2.14) . Выражение для толщины в случае круглого диска может быть записано в следующем виде:
. Выражение для толщины в случае круглого диска может быть записано в следующем виде: (2.15)
(2.15) . (2.16)
. (2.16)


