Еквівалентна системаДля усунення першої суперечності в основній системі, тобто для усунення відмін у деформаціях, створимо еквівалентну систему, тобто надамо додатковим в’язям поки що невідомі переміщення – жорсткі вузли разом із «плаваючими» затисненнями повертаємо на кути, що дорівнюють дійсним кутам повороту вузлів системи від зовнішнього навантаження, а додатковим опорним стержням даємо поступальні переміщення, які до- рівнюють дійсним поступальним переміщенням вузлів вихідної системи. Таким чином, основними невідомими методу переміщень є кути повороту жорстких вузлів системи та незалежні поступальні переміщення її вузлів. Ці невідомі методу переміщень позначаються літерами Усунувши першу суперечність у деформаціях між вихідною розрахунковою схемою й основною системою створимо еквівалентну систему. Наприклад, для рами, що зображена на рис 1.1 (а) і 1.4 (а), яка тричі кінематично невизначувана, для усунення відмін у деформаціях вузлів надамо додатковим плаваючим в’язям (рис. 1.3, а, 1.4, б) невідомі кутові переміщення:
а) основна система; б) система з плаваючими в’язями; в) еквівалентна система Рисунок 1.4 – Отримання еквівалентної системи для рами 1
Для рами, що зображена на рис. 1.2 (а), 1.3 (б), 1.4 (а), яка тричі кінематично невизначувана, еквівалентна система показана на рис. 1.5 (в).
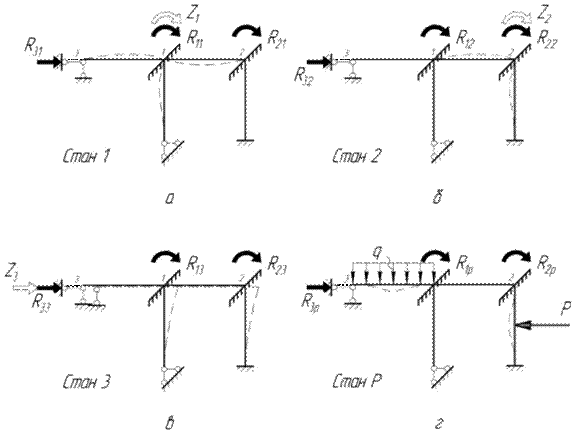
а) основна система; б) система з плаваючими в’язями; в) еквівалентна система Рисунок 1.5 – Отримання еквівалентної системи для рами 2 1.4 Розв’язувальні рівняння методу переміщень (канонічні рівняння) Для складання розв’язувальних рівнянь методу переміщень використовуємо другу суперечність між вихідною розрахунковою схемою та її основною системою. Вона полягає в тому, що в додаткових в’язях основної системи від зовнішнього навантаження виникають реактивні сили в додаткових опорних стержнях, а в «плаваючих» затисненнях жорстких вузлів – реактивні моменти, тобто виникають реакції, яких немає у вихідній системі через відсутність цих додаткових в’язей. Отже, необхідно скласти математичні умови рівності нулю відповідних реактивних сил у накладених додаткових в’язях у стані навантаження основної системи кутами повертання жорстких вузлів із «плаваючими» затисненнями, поступальними переміщеннями вузлів зі встановленим опорним стержнем у його напрямі та зовнішнім навантаженням. Так, наприклад, для рами (рис. 1.4), яка тричі кінематично невизначувана, розглянемо окремі стани основної системи (рис. 1.6), у кожному з яких на неї діє один фактор (рис. 1.6).
а) стан 1; б) стан 2; в) стан 3; г) стан Р Рисунок 1.6 – Окремі стани основної системи
У стані 1 (рис. 1.6, а) жорсткий вузол 1 повертається разом із «плаваючим» затисненням на кут, що дорівнює У кожному стані в усіх додаткових в’язях виникають реактивні сили. Вводимо для цих реактивних сил позначення На підставі принципу суперпозиції сумарний реактивний момент у першому (1) рухомому затисненні від усіх невідомих переміщень (
Сумарний реактивний момент у другому (2) затисненні від усіх невідомих переміщень (
Сумарна реакція в додатковому опорному стержні (третя додаткова в’язь) від усіх невідомих переміщень (
Але у вихідній рамі ці додаткові в’язі відсутні. Тому для еквівалентності напружено-деформованого стану основної системи і вихідної схеми рами прирівняємо до нуля сумарні реактивні сили у додаткових в’язях:
Реактивні сили у додаткових в’язях від невідомого переміщення, що дорівнює одиниці (
Перепишемо сумарні реактивні сили в усіх станах, з урахуванням одиничних реактивних сил для розглянутої рами:
Ця сукупність залежностей є розв’язувальними рівняннями методу переміщень і називаються системою канонічних рівнянь методу переміщень. Кількість отриманих рівнянь дорівнює кількості додаткових в’язей, тобто ступеню кінематичної невизначуваності системи, яка також дорівнює кількості основних невідомих методу переміщень ( Фізичний зміст кожного з цих рівнянь полягає в тому, що сумарна реактивна сила у відповідній додатковій в’язі основної системи від усіх невідомих переміщень та зовнішнього навантаження дорівнює нулю. Система розв’язувальних рівнянь методу переміщень може бути записана в матричному вигляді як:
де
Коефіцієнти Коефіцієнти Для визначення коефіцієнтів та вільних членів системи канонічних рівнянь необхідно мати епюри внутрішніх зусиль в основній системі методу переміщень в одиничних та вантажному станах.
|

 (і = 1, 2, 3…).
(і = 1, 2, 3…). ,
, 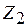 (кути повороту вузлів 1, 2), та
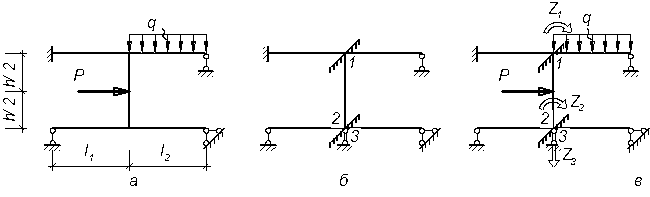
(кути повороту вузлів 1, 2), та 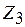 – поступальне переміщення цих вузлів при зовнішньому навантаженні вихідної системи, і одержимо еквівалентну систему (рис. 1.4, в).
– поступальне переміщення цих вузлів при зовнішньому навантаженні вихідної системи, і одержимо еквівалентну систему (рис. 1.4, в).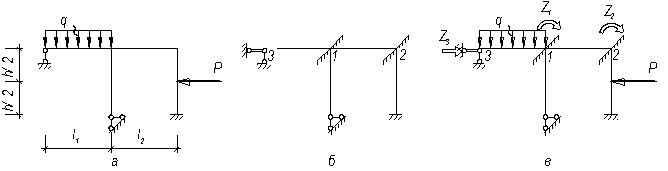
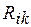 – перший індекс
– перший індекс  відповідає номеру додаткової в’язі, де виникає ця реакція, тобто номеру невідомого переміщення цієї в’язі, другий індекс
відповідає номеру додаткової в’язі, де виникає ця реакція, тобто номеру невідомого переміщення цієї в’язі, другий індекс  відповідає номеру стану, в якому виникає реакція. Наприклад
відповідає номеру стану, в якому виникає реакція. Наприклад  – реактивний момент вузла 2 у стані 3.
– реактивний момент вузла 2 у стані 3.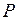 ) дорівнює сумі відповідних реактивних моментів в усіх станах (рис. 1.6):
) дорівнює сумі відповідних реактивних моментів в усіх станах (рис. 1.6):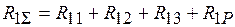 .
.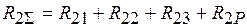 .
.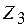 ) і зовнішнього навантаження (
) і зовнішнього навантаження (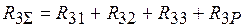 .
. ;
; 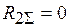 ;
; 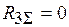 .
. ;
;  ;
;  ), називають одиничними реактивними силами. Позначимо їх
), називають одиничними реактивними силами. Позначимо їх  . Тоді має місце співвідношення:
. Тоді має місце співвідношення: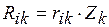 .
. ;
; ;
;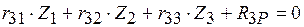 .
.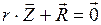 ,
,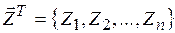 − вектор основних невідомих переміщень;
− вектор основних невідомих переміщень;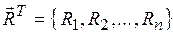 − вектор вантажних реакцій;
− вектор вантажних реакцій;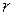 − матриця одиничних коефіцієнтів системи розв’язувальних рівнянь:
− матриця одиничних коефіцієнтів системи розв’язувальних рівнянь: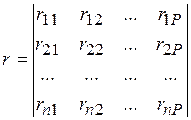 .
.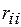
 , що розташовуються на головній діагоналі матриці коефіцієнтів системи рівнянь, називаються головними одиничними коефіцієнтами (реакціями). Їхні величини тільки додатні й не дорівнюють нулю.
, що розташовуються на головній діагоналі матриці коефіцієнтів системи рівнянь, називаються головними одиничними коефіцієнтами (реакціями). Їхні величини тільки додатні й не дорівнюють нулю.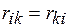 ).
).


