SOLUTIONS PRE-INTERMEDIATE
Вопрос № 202 $$1 Test the function of two variables on extreme points: (0;-2) min
Вопрос № 203 $$1 Test the function of two variables on extreme points: (2;-3)local min Вопрос № 204 $$1 Test the function of two variables on extreme points: (-4;-2)local max Вопрос № 205 $$1 Test the function of two variables on extreme points: (2;3) saddle point
1. $$1 Determine the domain of the function:
$$2
$$3
$$4
$$5
$$6
2. $$1 Find the limit of the function:
$$2 4
$$3 0
$$4
$$5 -4
$$6 2
3.
$$1 Take derivative of the function:
$$2
$$3
$$4
$$5
$$6
4. $$1 Find the interval where the function is increasing:
$$2
$$3
$$4
$$5 $$6
5. $$1 Find the extreme points of the function:
$$2 y(1)-max and y(3) -min
$$3 y(1)-min and y(3) -max
$$4 y(-1)-min and y(-3) -max
$$5 y(-1)-min and y(-3) -max
$$6 y(-4)-max and y(3) –min
6.
$$1 Find the interval where the function is concave:
$$2
$$3
$$4
$$5
$$6
7.
$$1 Find the points of inflection of the function:
$$2 y(2)
$$3 y(-2)
$$4 y(1) and y(3)
$$5 y(-3)
$$6 y(-3) and y(-1)
8.
$$1 Find the equations of the vertical asymptotes of the function:
$$2 x = -3 and x=3
$$3 x= 2
$$4 x= 2/9
$$5 y= -3 and y=3 $$6 y= 2x-3
9. $$1 Find the equations of the horizontal asymptotes of the function:
$$2 y=2
$$3 x= 2
$$4 y= 2/9
$$5 y= -3 and y=3
$$6 y= 2x-3
10. $$1 Find the partial derivative
$$2
$$3
$$4
$$5
$$6
11.
$$1 Evaluate the indefinite integral:
$$2
$$3
$$4
$$5
$$6
12.
$$1 Formula of Integration by parts is:
$$2
$$3
$$4
$$5
$$6
13.
$$1 What property of indefinite integrals is wrong:
$$2
$$3
$$4
$$5
$$6
14.
$$1 Find the area bounded between two curves:
$$2 32/3
$$3 2/9
$$4 4/3
$$5 1
$$6 -1/2
15.
$$1 Average value over interval (a; b) of continuous function is defined by integral: Find the average demand of the function: D(x) =
$$2 6
$$3 1
$$4 8
$$5 12/7
$$6 25/3
16.
$$1 Find the general solution of differential equation:
$$2
$$3
$$4
$$5
$$6
17.
$$1 Find general solution of differential equation:
$$2
$$3
$$4
$$5
$$6
18.
$$1 Evaluate the iterated integral:
$$2 23/3
$$3 2/5
$$4 15/4
$$5 1
$$6 ½
19. $$1 Reduce the double integral to iterated integral: D -region is depicted
$$2
$$3
$$4
$$5
$$6
20. $$1 Take the limit using L,Hopital,s rule:
$$2
$$3 1/3
$$4 5
$$5 7 $$6 5/3
21.
$$1 Take the limit using L,Hopital,s rule:
$$2
$$3 12
$$4 ln5
$$5 4/5
$$6 12/5
22.
$$1 Take the limit using L,Hopital,s rule:
$$2
$$3 2
$$4 3
$$5 6
$$6 3/2
23.
$$1 Take the indefinite integral:
$$2
$$3
$$4
$$5
$$6
24.
$$1 Take the indefinite integral:
$$2
$$3
$$4
$$5
$$6
25.
$$1 Take the indefinite integral:
$$2
$$3
$$4
$$5
$$6
26.
$$1 Take the indefinite integral:
$$2
$$3
$$4
$$5 $$6
27. $$1 Take the indefinite integral:
$$2
$$3
$$4
$$5
$$6
28.
$$1 Which of the following functions is inverse to the function:
$$2
$$3
$$4
$$5 $$6
29.
$$1 Which of the following functions are odd functions: a)
$$2 b) and c)
$$3 a)
$$4 e)
$$5 a) and c)
$$6 no one
30.
$$1 Take differential of the function:
$$2
$$3
$$4
$$5
$$6
31.
$$1 Test the function of two variables on extreme points: It is known that It is known that If at critical point: a) b) d)
$$2
$$3
$$4 $$5
$$6 test fails
32.
$$1 Find the general term of the number series:
$$2
$$3
$$4
$$5
$$6
33.
$$1 Let given two series: If for any n: un ≤ vn, then a) from convergence of b)from divergence of The test is known as:
$$2 Comparison test
$$3 Ratio test
$$4 Root test
$$5 Integral test
$$6 Necessary test for convergence
34.
$$1 Let for a) the series converges if b) the series diverges if c) the test fails if The test is known as:
$$2 Ratio test
$$3 Comparison test
$$4 Root test
$$5 Integral test
$$6 Necessary test for convergence
35.
$$1 Let for a) the series converges if b) the series diverges if c) the test fails if The test is known as:
$$2 Root test
$$3 Comparison test
$$4 Ratio test
$$5 Integral test
$$6 Necessary test for convergence
36.
$$1 Let un=f(n) (f(x) is continuous and positive). Then the The test is known as:
$$2 Integral test
$$3 Comparison test
$$4 Ratio test
$$5 Root test
$$6 Necessary test for convergence
37.
$$1 What series among harmonic series is/are convergent: a)
$$2 d)
$$3 a)
$$4 b)
$$5 c)
$$6 e)
38.
$$1 What series among harmonic series is/are divergent: a)
$$2 a)
$$3 d)
$$4 b)
$$5 c)
$$6 e)
39.
$$1 What series among following series is/are convergent: a)
$$2 b) and e)
$$3 a) and c)
$$4 b) and d)
$$5 c) and a) and d)
$$6 c) and d)
40.
$$1 What series among following series is/are divergent: a)
$$2 a) and c) and d)
$$3 b) and e)
$$4 b) and d)8
$$5 c) and e) and d)
$$6 c) and d)
41.
$$1 Determine the interval of convergence with radius
$$2
$$3
$$4
$$5 everywhere convergent
$$6 everywhere divergent
42.
$$1 Determine the interval of convergence with radius
$$2
$$3
$$4
$$5 everywhere convergent
$$6 everywhere divergent
43.
$$1 What series among following alternating series is/are divergent: a)
$$2 a) and c) and d)
$$3 b) and e)
$$4 b) and d)
$$5 c) and e) and d)
$$6 c) and d)
44.
$$1 What series among following alternating series is/are convergent absolutely: a)
$$2 b) and e)
$$3 a) and c) and d)
$$4 b) and c)and e)
$$5 c) and e) and d)
$$6 c) and d)
45.
$$1 What series among following alternating series is/are convergent conditionally: a)
$$2 a) and c)
$$3 a) and b) and c) and d)
$$4 b) and c)and e)
$$5 c) and e) and d)
$$6 e)
SOLUTIONS PRE-INTERMEDIATE
|



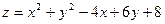

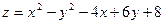






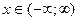


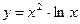
 2 x lnx + x
2 x lnx + x

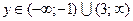











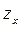 of the function of two variables:
of the function of two variables: 













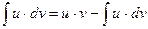






 if
if 

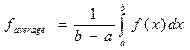 .
.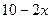 if x -output is changed:
if x -output is changed:  .
.


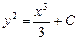

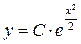







 .
.








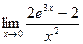







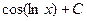








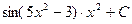
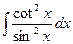





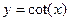
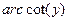




 ; b)
; b)  ; c)
; c)  d)
d)  e)
e) 
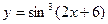
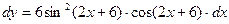





 - Heissian > 0 and
- Heissian > 0 and  =>
=> 
 =>
=>  ; c)
; c)  - saddle point;
- saddle point;





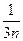



 and
and 
 , then
, then ;
; ;
; .
. , then
, then both are convergent or divergent.
both are convergent or divergent.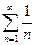 ; b)
; b)  ; c)
; c)  ; d)
; d)  ; e)
; e) 
 ; b)
; b) 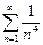 ; c)
; c)  ; d)
; d) 
 ; b)
; b)  ; c)
; c)  ; d)
; d)  ; e)
; e) 
 of the following power series:
of the following power series: 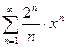



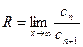 of the following power series:
of the following power series: 


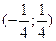
 ; b)
; b)  ; c)
; c)  ; d)
; d)  ; e)
; e) 
 ; d)
; d) 
 ; b)
; b)  ; c)
; c)  ; e)
; e) 



