Головна сторінка Випадкова сторінка
КАТЕГОРІЇ:
АвтомобіліБіологіяБудівництвоВідпочинок і туризмГеографіяДім і садЕкологіяЕкономікаЕлектронікаІноземні мовиІнформатикаІншеІсторіяКультураЛітератураМатематикаМедицинаМеталлургіяМеханікаОсвітаОхорона праціПедагогікаПолітикаПравоПсихологіяРелігіяСоціологіяСпортФізикаФілософіяФінансиХімія
Від чого помирає більша частина дітей при типі смертності немовлят А?
Дата добавления: 2014-12-06; просмотров: 687
|
|
Определение. Непрерывной называют случайную величину Х, функцию распределения которой F(x) можно представить в виде
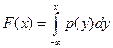
Функцию р(х) называют плотностью распределения (вероятностей) случайной величины X.
Плотность распределения случайной величины обычно является непрерывной (за исключением, быть может, конечного числа точек) функцией. Следовательно, функция распределения для непрерывной случайной величины является непрерывной на всей числовой оси и в точках непрерывности плотности распределения p(х) имеет место равенство
p(x) = F'(x)
что следует из свойств интеграла с переменным верхним пределом.
Теорема. Плотность распределения обладает следующими свойствами:
1) 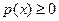 ;
;
2) 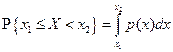 ;
;
3) 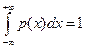 ;
;
4) 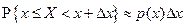 в точках непрерывности плотности распределения;
в точках непрерывности плотности распределения;
5) 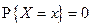 .
.
Доказательство. 1) Утверждение 1 следует из того, что плотность распределения является производной от функции распределения, в силу свойства 1 функции распределения она является неубывающей функцией, а производная неубывающей функции неотрицательна.
2) Второе утверждение следует из свойства 2 функции распределения и свойств несобственного интеграла
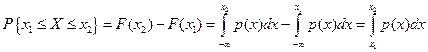 3) В частности, при
3) В частности, при 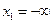 , , 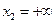 событие событие 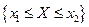 является достоверным, и поэтому справедливо утверждение 3.
4) является достоверным, и поэтому справедливо утверждение 3.
4) 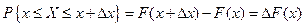 . Если . Если 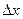 мало, то мало, то
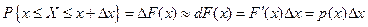 5) Поскольку в силу определения функция распределения случайной величины есть несобственный интеграл от плотности, то она является непрерывной, откуда следует утверждение 5.
5) Поскольку в силу определения функция распределения случайной величины есть несобственный интеграл от плотности, то она является непрерывной, откуда следует утверждение 5.
|
Примеры непрерывные случайных величин
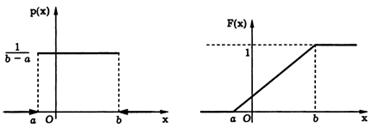
Равномерное распределение. Случайная величина имеет равномерное распределение на отрезке [а, b], если ее плотность распределения
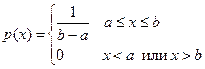 ,
, 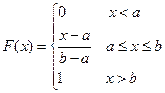
Вероятность попадания равномерно распределенной случайной величины в интервал (х1, x2), лежащий внутри отрезка [a, b], равна F(x2) − F(x1) = (x2 − x1)/(b − а), т.е. пропорциональна длине этого интервала. Таким образом, равномерное распределение реализует схему геометрической вероятности при бросании точки на отрезок [a, b].
Экспоненциальное распределение. Случайная величина распределена по экспоненциальному (показательному) закону, если она имеет плотность распределения
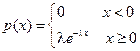 ,
, 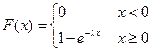
где λ > 0 − параметр экспоненциального распределения.
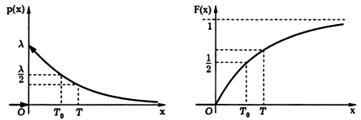
Экспоненциально распределенная случайная величина может принимать только положительные значения. Примером случайной величины, имеющей экспоненциальное распределение, является время распада радиоактивных элементов.
Экспоненциально распределенная случайная величина X обладает весьма важным свойством, которое естественно назвать отсутствием последействия. Трактуя X как время распада атома, рассмотрим событие
A = {xi < X < х1 + x2}
и найдем условную вероятность этого события при условии выполнения события В = {X > х1}. В соответствии с определением условной вероятности P(A|B) = P(AB)/P(B). Но событие AB,как нетрудно понять, совпадает с событием А. Поэтому P(A|B) = P(A)/P(B). Далее, используя свойство 4 функции распределения, имеем: 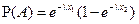 , , 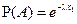 . Значит, . Значит, 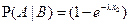 , то есть вероятность распада атома за время х2 при условии, что перед этим он уже прожил время х1, совпадает с безусловной вероятностью распада того же самого атома за время x2. Именно это свойство и представляет собой отсутствие последействия. Допуская некоторую вольность речи, отсутствие последействия можно трактовать как независимость остаточного времени жизни атома от того времени, которое он уже прожил. Можно показать и обратное: если случайная величина X обладает свойством отсутствия последействия, то она обязательно должна быть распределена по экспоненциальному закону. Таким образом, отсутствие последействия является характеристическим свойством экспоненциально распределенных случайных величин. , то есть вероятность распада атома за время х2 при условии, что перед этим он уже прожил время х1, совпадает с безусловной вероятностью распада того же самого атома за время x2. Именно это свойство и представляет собой отсутствие последействия. Допуская некоторую вольность речи, отсутствие последействия можно трактовать как независимость остаточного времени жизни атома от того времени, которое он уже прожил. Можно показать и обратное: если случайная величина X обладает свойством отсутствия последействия, то она обязательно должна быть распределена по экспоненциальному закону. Таким образом, отсутствие последействия является характеристическим свойством экспоненциально распределенных случайных величин.
|
Нормальное распределение. Случайная величина распределена по нормальному (или гауссову) закону, или имеет нормальное (гауссово) распределение, если ее плотность
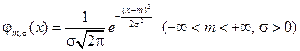
Нормальное распределение зависит от двух параметров: m, называемого математическим ожиданием или средним значением, и σ, называемого средним квадратичным отклонением.
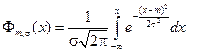
Если m = 0 и σ = 1, то такой нормальный закон называют стандартным и его функцию распределения обозначают Ф(x), а плотность распределения − φ(х). С плотностью и функцией стандартного нормального распределения мы уже встречались в локальной и интегральной формулах Муавра−Лапласа.