Консультативні фірми

Дата добавления: 2015-08-17; просмотров: 698

Задняя поверхность призматических фасонных резцов представляет собой цилиндрическую поверхность, образующие которой параллельны базе крепления, а направляющей служит режущая кромка, лежащая в передней поверхности. Для вывода уравнения задней поверхности призматического резца расположим систему координат S₂ так, чтобы оси z₀ и z₂ совпадали, ось у₀ совпадала с образующей задней поверхности в базовой точке, ось х₂ была перпендикулярна осям у₂ и z₂. При таком расположении система S₂ повернута вокруг оси z₂ на угол α+γ относительно S₀ (рис. 13).

Рис. 13. К выводу уравнений профиля

призматического резца

Уравнения задней поверхности призматического резца:

(1.14)

Профилем фасонного резца называют линию сечения задней поверхности плоскостью, перпендикулярной ее образующим. Поскольку образующие параллельны оси у₂, то любое сечение задней поверхности плоскостью у₂ = const определяет профиль резца. Полагая, что у₂=0, для определения координат профиля получаем уравнения:

(1.15)

Решая совместно уравнения (1.13), (1.11), (1.12), и (1.15) при переменных значениях R_i и 1_i, определяют размеры профиля призматического резца. Задняя поверхность круглого радиального фасонного резца представляет собой поверхность вращения. Образование ее можно представить следующим образом.

Передняя поверхность резца (плоскость П, в которой расположена режущая кромка) отстоит от оси резца на расстоянии Н =R sin (α + γ) (рис. 14). Если на переднюю поверхность опустить перпендикуляр S₂A, жестко связанный с ней в точке А, то при вращении его вокруг оси резца режущая кромка 1, лежащая в плоскости П, опишет заднюю поверхность. Передняя поверхность П круглого фасонного резца в любом ее положении будет касательной к цилиндру радиусом Н. Это свойство используется при заточке резца.

Рис. 14. К выводу уравнений профиля круглого резца

Угол τ, определяющий положение перпендикуляра S₂A в системе координат S₂, является параметром вращения.

Семейство поверхностей детали в системе S₂ получим, преобразовав уравнения (1.11):

(1.16)

Уравнение связи параметров точек профиля круглого резца получаем, рассекая уравнение семейства (1.16) плоскостью, проходящей через ось z₂. Приняв в качестве секущей плоскость у₂ =0, из второго уравнения системы (1.16) получим

(1.17)

Уравнения (1.16) примут вид

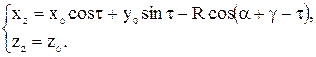(1.18)

Решая совместно уравнения (1.13), (1.11), (1.12), и (1.18) при переменных значениях R_i и 1_i, определяют координаты точек профиля круглого резца.