
Головна сторінка Випадкова сторінка
КАТЕГОРІЇ:
АвтомобіліБіологіяБудівництвоВідпочинок і туризмГеографіяДім і садЕкологіяЕкономікаЕлектронікаІноземні мовиІнформатикаІншеІсторіяКультураЛітератураМатематикаМедицинаМеталлургіяМеханікаОсвітаОхорона праціПедагогікаПолітикаПравоПсихологіяРелігіяСоціологіяСпортФізикаФілософіяФінансиХімія
Білет № 9
Дата добавления: 2015-08-17; просмотров: 664
|
|
Тема 5. Производная и дифференциал
[2] гл. IX, § 1—5; [3] № 907, 908, 910;
[2] гл. X; [3] № 850, 857, 875, 888, 945, 956
[2] гл. XII; [3] № 1067, 1075, 1077.
Разберите решение задачи 8 данного пособия.
Задача 8. Найдите производные функции:
а)у=In (2+sin 3х) ; б) у=(3  +1)
+1)  ;
;
в) cos (ху 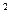 )-3у
)-3у 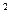

Решение: а) Последовательно применяя правилодифференцирования сложной функции, правила и формулы дифференцирования, имеем:
у'=  '=
'=  '=
'=  '+(sin3х)'
'+(sin3х)' 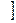 =
= 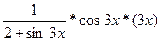 '=
'=  ;
;
б)у'=  '=4(3
'=4(3  +1)
+1) 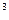 *(3
*(3  +1)'=4(3
+1)'=4(3  +1)
+1) 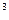 *3
*3  *In3*(arctg
*In3*(arctg 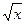 )'=
)'=
=4(3  +1)
+1) 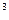 * 3
* 3  *In3*
*In3*  *
*  '=
'=  *3
*3  *(3
*(3  +1)
+1) 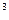 ;
;
в) В данном случае функциональная зависимость задана в неявном виде. Для нахождения производнойу' нужно продифференцировать по переменнойх обе части уравнения, считая при этому функцией отх, а затем полученное уравнение разрешить относительноу':
-sin (ху 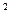 )*(ху
)*(ху 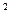 )'-6уу'+4=0,
)'-6уу'+4=0,
-sin (ху 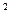 )*(у
)*(у 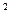 +2хуу')-6уу'+4=0,
+2хуу')-6уу'+4=0,
-у 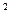 sin (ху
sin (ху 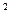 )-2хуу' sin (ху
)-2хуу' sin (ху 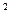 )-6уу'+4=0.
)-6уу'+4=0.
Из последнего уравнения находиму':
2уу'  х sin (ху
х sin (ху 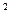 )+3
)+3 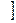 =4- у
=4- у 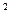 sin (ху
sin (ху 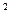 ),
),
у'= 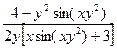 .
.
Вопросы для самопроверки
- Что называется производной функции?
- Каков геометрический, физический смысл производной?
- Как взаимосвязаны непрерывность функции и ее дифференцируемость в точке?
- Напишите основные правила дифференцирования функций.
- Напишите формулы дифференцирования основных элементарных функций.
- Сформулируйте правило дифференцирования сложной функции.
- Что называется дифференциалом функции?
- Каков геометрический смысл дифференциала функции.
- Перечислите основные свойства дифференциала функции.
- Напишите формулу, позволяющую находить приближенное значение функции при помощи ее дифференциала.
- Как найти производную второго, третьего, n-го порядков?
- Как найти дифференциал второго порядка от данной функции?
| <== предыдущая лекция | | | следующая лекция ==> |
| Білет № 8 | | | Р-н NaCl, |