
Головна сторінка Випадкова сторінка
КАТЕГОРІЇ:
АвтомобіліБіологіяБудівництвоВідпочинок і туризмГеографіяДім і садЕкологіяЕкономікаЕлектронікаІноземні мовиІнформатикаІншеІсторіяКультураЛітератураМатематикаМедицинаМеталлургіяМеханікаОсвітаОхорона праціПедагогікаПолітикаПравоПсихологіяРелігіяСоціологіяСпортФізикаФілософіяФінансиХімія
Р-н NaCl,
Дата добавления: 2015-08-17; просмотров: 618
|
|
[2] гл. XXVI § 3.
Задача 23. Предприятие имеет возможность приобрести не более 20 трехтонных и не более 18 пятитонных автомашин. Отпускная цена трехтонного грузовика 4000 руб., пятитонного - 5000 руб. Сколько нужно приобрести автомашин каждой марки, чтобы их суммарная грузоподъемность была максимальной, если для приобретения автомашин выделено 150 тысяч рублей? Задачу решить графическим и аналитическим методами.
Решение. Пусть приобретено х1 трехтонных и х2 пятитонных автомашин. Из условия задачи имеем
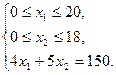 (1)
(1)
Суммарная грузоподъемность приобретенных грузовиков равна
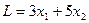 (2)
(2)
Задача состоит в нахождении такого решения системы (1), при котором линейная форма (целевая функция) (2) принимает наибольшее значение
Графический метод решения
В прямоугольной системе координат 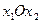 построим многоугольник ОАВСD, образованный прямыми
построим многоугольник ОАВСD, образованный прямыми 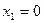 (OD),
(OD), 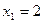 (АВ),
(АВ), 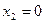 (АО),
(АО), 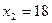 (СD) ,
(СD) , 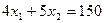 (ВС) и прямую
(ВС) и прямую 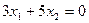 (L) (рис.9).
(L) (рис.9).
Системе (1) удовлетворяют координаты точек, лежащих на пятиугольнике ОАВСD и внутри него. Так как прямые (L) и ВС не параллельны, то для нахождения оптимального решения системы (1), для которого линейная форма (2) принимает наибольшее значение, достаточно найти значения этой формы в точках А, В, С, D и из полученных чисел выбрать наибольшее. В нашей задаче эти точки имеют следующие координаты: А(20; 0), В(20; 14), С(15; 18), D(0; 18). Подставляя координаты этих точек в (2), получим:
L(A)=L(20;0)=60; L(В)=L(20;14)=130;
L(С)=L(15;18)=135; L(D)=L(0;18)=90.

|
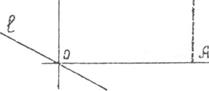 Р и с. 9
Р и с. 9
|
Следовательно, Lmax=L(15;18)=135, то есть предприятию
следует приобрести 15 трехтонных и 18 пятитонных автомашин.
Аналитический метод решения
В систему (1) введем дополнительные неизвестные х3 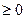 и х4
и х4 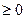 , чтобы она приняла следующий вид:
, чтобы она приняла следующий вид:
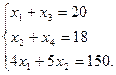 (3)
(3)
Система (3) имеет 3 уравнения и 4 неизвестные. Примем, например,х1 , х2, х3 за базисные неизвестные, а х4 — за свободное неизвестное и выразим из системы (3) неизвестные х1 , х2, х3 через х4. Тогда
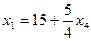 ,
, 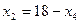 ,
, 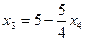 и
и
L= 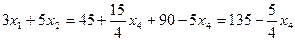 .
.
Из последнего выражения следует, что L принимает наибольшее значение при х4 =0 (так как х4 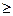 0). При х4 = 0 имеем:
0). При х4 = 0 имеем:
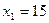 ,
, 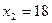 и L(15;18)=135.
и L(15;18)=135.
Следовательно, предприятие должно приобрести 15 трехтонных и 18 пятитонных автомашин при их общей грузоподъемности 135 тонн.
Вопросы для самопроверки
1. Сформулируйте основную задачу линейного программирования. Приведите примеры.
2. Дайте геометрическую интерпретацию основной задачи линейного программирования.
3. В чем суть симплекс-метода решения задач линейного программирования?
| <== предыдущая лекция | | | следующая лекция ==> |
| ВИДІЛЕННЯ З БАЗИ | | | ПР НАВИЧКИ КРОВООБІГ |