Words and word-combinations

Дата добавления: 2015-08-17; просмотров: 557

В рассматриваемом примере требуется построить сечение цилиндра плоскостью общего положения α, определить натуральную величину сечения и построить полную развертку усеченной части цилиндра.

Как и в ранее рассмотренных примерах, преобразуем чертеж так, чтобы плоскость α стала проецирующей. Используем способ
замены плоскостей проекций.

x₁₂ x₁₄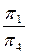

π₄┴π₁; π₄┴ α x₁₄┴ h₁

Сечение боковой поверхности цилиндра представляет собой эллипс. На плоскости проекций π₄ проекция сечения вырождается в от­резок прямой, принадлежащей следу плоскости απ₄. Найдем опорные точки сечения: концы большой и малой осей эллипса, точке видимости. Поскольку ось цилиндра перпендикулярна горизонталь­ной плоскости проекций, то проекция его боковой поверхности вырождается на плоскость π₁ в окружность. Горизонтальная проекция фигуры сечения (эллипс) совпадает с вырожденной проекци­ей боковой поверхности цилиндра на плоскости π₁. Фронтальную проекцию сечения строим по принадлежности его точек образующим цилиндра.

Большая ось эллипса – сечения (отрезок-15) располагается на линии ската плоскости α, малая ось (отрезок-37) – на го­ризонтали этой плоскости. Точки видимости 2 и 6 лежат на очерковых образующих цилиндра. Находим их проекции сначала в систе­ме плоскостей 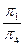, а затем строим их фронтальные проекции по принадлежности соответствующим образующим цилиндра.

Натуральную величину фигуры сечения определяем способом плоскопараллельного перемещения. Построение эллипса по большой и малой оси показано в приложении 4.

Для построения развертки боковой поверхности цилиндра в не­го вписана восьмигранная прямая призма. Затем выполнена разверт­ка этой призмы методом нормального сеченая, так как ребра её перпендикулярны плоскости π₁, а основание представляет собой натуральную величину нормального сечения.

На прямой откладываем отрезки, равные хордам дуг [1₁ 2₁], [2₁ 3₁] … [1₁ 8₁] через полученные точки проводим перпендикуляры и откладываем на них отрезки, равные высоте точек 1,2…8 над плоскостью π₁ (высота точки берется с фронтальной плоскости проекций). Полученные точки соединяются плавной кривой (синусоидой), используя лекало. Достраиваем верхнее и нижнее основания усеченной части цилиндра.