ЗАТВЕРДЖЕНО

Дата добавления: 2015-08-17; просмотров: 671

Использование метода сил для расчета систем с высокой степенью статической неопределимости связано с решением совместной системы большого количества линейных уравнений. Даже самый экономичных метод решения таких систем – алгоритм Гаусса – требует 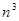вычислительных операций (где n – число уравнений, т.е. степень статической неопределимости системы), при условии, что все коэффициенты системы отличны от нуля. 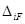В связи с этим нужно стремиться так выбрать основную систему, чтобы возможно большее число побочных единичных перемещений и свободных членов обратилось в ноль.

Основным средством для достижения этой цели является использование симметрии. Стержневая система является симметричной, если симметричны не только оси и опорные закрепления (геометрическая симметрия), но и жесткости (упругая симметрия). При этом внешняя нагрузка может быть и несимметричной.

При выборе основной системы лишние неизвестные следует выбирать в виде симметричных и обратно симметричных усилий. Симметричные неизвестные создают симметричные эпюры моментов, а обратно симметричные неизвестные – кососимметричные эпюры. Такие эпюры обладают свойством взаимной ортогональности, т.е. результат их перемножения равен нулю:

(3.14)

Ортогонализация эпюр может достигаться различными способами:

1) выбор симметричной основной системы; 2) выбор симметричных и обратносимметричных неизвестных; 3) группировка неизвестных; 4) устройство жестких консолей (способ упругого центра); 5) использование статически неопределимой основной системы; 6) разложение произвольной нагрузки на симметричную и обратносимметричную составляющие.

Использование большинства этих способов будет рассмотрено ниже на конкретных примерах, здесь же охарактеризуем только способ, заключающийся в применении статически неопределимой основной системы. Для расчета статически неопределимой системы можно отбрасывать не все лишние неизвестные, а одно или несколько. При этом уменьшается число канонических уравнений. Так, рассчитывая n раз статически неопределимую систему, можно не решать n уравнений, если в качестве основной системы применять систему со степенью статической неопределимости n -1. Для определения усилия в i-ой удаленной связи достаточно решить лишь одно уравнение:

где и 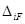- перемещения по направлению 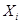в основной, (n-1) раз статически неопределимой системе, вызываемые усилием 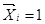и внешней нагрузкой соответственно.

Следовательно, рассматриваемый способ требует, чтобы предварительно были вычислены все необходимые перемещения в статически неопределимой основной системе. Для этого необходимо заранее иметь эпюры внутренних усилий от действия на статически неопределимую основную систему единичных неизвестных и заданной внешней нагрузки. Если же таких эпюр нет, то расчет не только не упростится, но даже может усложниться. Это обстоятельство резко ограничивает практическую область применения рассмотренного способа.