
Головна сторінка Випадкова сторінка
КАТЕГОРІЇ:
АвтомобіліБіологіяБудівництвоВідпочинок і туризмГеографіяДім і садЕкологіяЕкономікаЕлектронікаІноземні мовиІнформатикаІншеІсторіяКультураЛітератураМатематикаМедицинаМеталлургіяМеханікаОсвітаОхорона праціПедагогікаПолітикаПравоПсихологіяРелігіяСоціологіяСпортФізикаФілософіяФінансиХімія
МІНІСТЕРСТВО ОХОРОНИ ЗДОРОВЯ УКРАЇНИ
Дата добавления: 2015-08-29; просмотров: 671
|
|
«Уравнение Бернулли имеет чрезвычайно важное значение в гидравлике, позволяя по двум известным элементам их трех ( 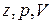 ) определить третий. Нередко это уравнение является наиболее действительным средством как для исследования различных теоретических вопросов гидравлики, так и для решения многих практических задач, выдвигаемых инженерной практикой, а поэтому его можно считать фундаментальным для гидравлики уравнением движения», - так определил значение уравнения Бернулли академик Н.Н.Павловский.
) определить третий. Нередко это уравнение является наиболее действительным средством как для исследования различных теоретических вопросов гидравлики, так и для решения многих практических задач, выдвигаемых инженерной практикой, а поэтому его можно считать фундаментальным для гидравлики уравнением движения», - так определил значение уравнения Бернулли академик Н.Н.Павловский.
С помощью уравнения Бернулли легко объяснить ряд явлений, наблюдаемых в технике и повседневной жизни. Так, например, очень легко установить характер распределения давлений в горизонтальной трубе переменного сечения (рис. II.06). Действительно, применяя уравнение неразрывности к двум сечениям, показанным на рисунке, устанавливаем, что в узкой части поток обладает большими средними скоростями, чем в широкой части:  и
и  , поэтому
, поэтому  .
.
Запишем уравнение Бернулли для этих же сечений потока. Это воз  можно сделать, так как движение вблизи выбранных сечений удовлетворяет условиям плавно изменяющегося движения. Труба расположена горизонтально, и если выбрать для определения величин
можно сделать, так как движение вблизи выбранных сечений удовлетворяет условиям плавно изменяющегося движения. Труба расположена горизонтально, и если выбрать для определения величин  и
и 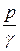 в сечениях 1-1 и 2-2 частицы жидкости, расположенные на ее оси. То для этих частиц значения
в сечениях 1-1 и 2-2 частицы жидкости, расположенные на ее оси. То для этих частиц значения 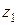 и
и 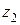 будут одинаковыми
будут одинаковыми  . пренебрегая величиной потерь на участке потока 1-2 (
. пренебрегая величиной потерь на участке потока 1-2 (  ) и неравномерностью распределения скоростей в сечениях (
) и неравномерностью распределения скоростей в сечениях (  ), запишем уравнение Бернулли в следующем виде:
), запишем уравнение Бернулли в следующем виде:
 .
.
Отсюда найдем:
 . (II.28)
. (II.28)
Но ранее было установлено, что  , поэтому разность
, поэтому разность  , и, следовательно, давление
, и, следовательно, давление  .
.
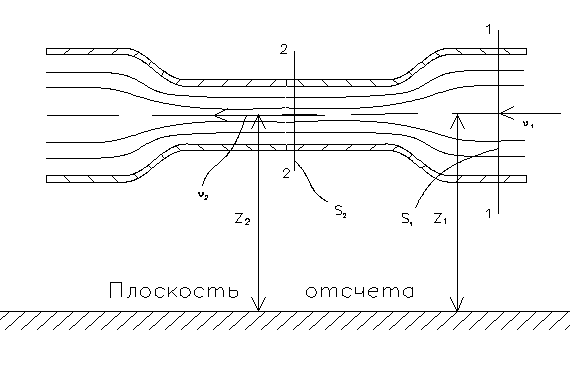
Рис. II.06.
Полученный результат подчеркивает специфическую особенность жидкостей преобразовывать кинетическую энергию давления (и наоборот), что очень хорошо используется в технике и находит самые разнообразные применения. Так, например, пропуская жидкость с большими скоростями через суженные сечения, можно значительно понизить в этом сечении давление и создать благоприятные условия для всасывания жидкости. Этот принцип используется для создания различных струйных аппаратов (водоструйных и пароструйных насосов и т.п.). Очень широко используется тот же принцип в измерительной технике для определения установившихся расходов жидкости и скоростей ее движения.
Рассмотрим так называемый водомер Вентури, который служит для измерения расхода жидкости и представляет собой короткий двухконусный патрубок, сначала суживающийся, а затем расширяющийся (рис. II.06.), вмонтированный в короткий трубопровод.
Записывая уравнение Бернули для сечений 1 и 2, получим при тех же предположениях, что и выше, зависимость (11.29), которую перепишем в виде:

Здесь h – разность уровней в пьезометрических трубках, присоединяемых к сечениям  и
и  .
.
Из уравнения неразрывности следует, что скорости в сечении 1 и 2 обратно пропорциональны площадям  и
и  , то есть
, то есть
 . (II.30)
. (II.30)
Представим выражение (11.30) таким образом:
 (II.31)
(II.31)
Отсюда


или с учетом (11.31),

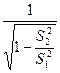

Рис. II.07.
Следовательно,
 (II.32)
(II.32)
Здесь k – константа водомера, постоянная для водомера заданной конструкции и размеров.
Скорость течения жидкости может быть измерена весьма простым прибором, называемым трубкой Пито. Этот прибор представляет собой согнутую под прямым углом трубку, открытый конец которой направляется против течения так, чтобы ее ось совпала с направлением вектора скорости. Если в точке потока, в которой измеряется скорость, предварительно измерить пьезометрический напор 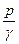 , а затем измерить гидродинамическое давление трубкой Пито, то тогда легко вычислить и величину скорости. Посмотрим, на какой уровень поднимется жидкость в трубке Пито. Составим уравнение Бернули для сечений вдали от трубки Пито и для ее открытого конца (рис. II.08.):
, а затем измерить гидродинамическое давление трубкой Пито, то тогда легко вычислить и величину скорости. Посмотрим, на какой уровень поднимется жидкость в трубке Пито. Составим уравнение Бернули для сечений вдали от трубки Пито и для ее открытого конца (рис. II.08.):

 (II.33)
(II.33)
Но скорость частиц жидкости, набегающих на неподвижную жидкость в конце трубки Пито, падает до нуля ( 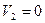 ), и они оказывают на жидкость в трубке Пито дополнительное давление, соответствующее потерянной кинетической энергии
), и они оказывают на жидкость в трубке Пито дополнительное давление, соответствующее потерянной кинетической энергии  . Действительно, из выражения (II.33) получим:
. Действительно, из выражения (II.33) получим:
 .
.

Рис. II.08.
Так как при получении зависимостей (II.31) для водомера Вентури и (II.33) для трубки Пито не учитывались потери напора, то результаты вычислений по этим формулам должны давать несколько завышенные, по сравнению с действительными, значения искомых величин. Поэтому в эти формулы обычно вводятся поправочные коэффициенты, находимые опытным путем.
Составитель Русинова Н.Г
| <== предыдущая лекция | | | следующая лекция ==> |
| Завдання 1. Вивчити патологічні та компенсаторні реакції організму при перегріванні. | | | Завдання 1. Вивчити патологічні та компенсаторні реакції організму при перегріванні. |