
Головна сторінка Випадкова сторінка
КАТЕГОРІЇ:
АвтомобіліБіологіяБудівництвоВідпочинок і туризмГеографіяДім і садЕкологіяЕкономікаЕлектронікаІноземні мовиІнформатикаІншеІсторіяКультураЛітератураМатематикаМедицинаМеталлургіяМеханікаОсвітаОхорона праціПедагогікаПолітикаПравоПсихологіяРелігіяСоціологіяСпортФізикаФілософіяФінансиХімія
СУТНІСТЬ ОРГАНІЗАЦІЇ ЗАРОБІТНОЇ ПЛАТИ
Дата добавления: 2015-08-30; просмотров: 544
|
|
Коэффициент асимметриипоказывает «скошенность» ряда распределения относительно центра:
 , (6.68)
, (6.68)
где 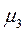 – центральный момент третьего порядка;
– центральный момент третьего порядка;
 – куб среднего квадратического отклонения.
– куб среднего квадратического отклонения.
Для данного метода расчета: если  , в распределении наблюдается правосторонняя (положительная асимметрия), если
, в распределении наблюдается правосторонняя (положительная асимметрия), если  , в распределении наблюдается левосторонняя (отрицательная асимметрия)
, в распределении наблюдается левосторонняя (отрицательная асимметрия)
Кроме центрального момента расчет асимметрия можно провести, используя моду или медиану:
 либо
либо  , (6.69)
, (6.69)
Для данного метода расчета: если 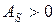 , в распределении наблюдается правосторонняя (положительная асимметрия), если
, в распределении наблюдается правосторонняя (положительная асимметрия), если  , в распределении наблюдается левосторонняя (отрицательная асимметрия) (рис. 4).
, в распределении наблюдается левосторонняя (отрицательная асимметрия) (рис. 4).

Рис. 4. Асимметричные распределения
Величина, показывающая «крутость» распределения, называется коэффициентом эксцесса:
 , (6.70)
, (6.70)
Если  , в распределении наблюдается островершинность – эксцесс положительный, если
, в распределении наблюдается островершинность – эксцесс положительный, если  , в распределении наблюдается плосковершинность – эксцесс отрицательный (рис. 5).
, в распределении наблюдается плосковершинность – эксцесс отрицательный (рис. 5).

Рис. 5. Эксцессы распределения
Пример 5.Имеются данные о количестве овец  по хозяйствам района (табл. 9).
по хозяйствам района (табл. 9).
Таблица 9
| № |  тыс.голов. тыс.голов.
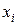
| № |  тыс.голов. тыс.голов.
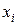
| № |  тыс.голов. тыс.голов.
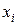
|
| 2,0 | 3,0 | 5,5 | |||
| 2,5 | 4,0 | 6,0 | |||
| 2,5 | 5,5 | 6,5 | |||
| 3,0 | 5,5 | 7,0 |
Рассчитать.
1. Среднее количество овец в расчете на одно хозяйство.
2. Моду.
3. Медиану.
4. Показатели вариации
· дисперсию;
· стандартное отклонение;
· коэффициент вариации.
5. Показатели асимметрии и эксцесса.
Решение.
1. Так как значение варианты  в совокупности повторяется по несколько раз, с определенной частотой
в совокупности повторяется по несколько раз, с определенной частотой  для расчета среднего значения используем формулу среднюю арифметическую взвешенную:
для расчета среднего значения используем формулу среднюю арифметическую взвешенную:

2. Данный ряд является дискретным, поэтому модой будет варианта с наибольшей частотой –  .
.
3. Данный ряд является четным, в этом случае медиану для дискретного ряда находят по формуле:

То есть, половина хозяйств в исследуемой совокупности имеют количество овец до 4,75тыс.голов. а половина свыше данной численности.
4. Для расчета показателей вариации составим таблицу 10, в которой рассчитаем отклонения  , квадраты данных отклонений
, квадраты данных отклонений  , расчет можно провести как по простым, так и по взвешенным формулам расчета (в примере используем простую):
, расчет можно провести как по простым, так и по взвешенным формулам расчета (в примере используем простую):
Таблица 10
| № | 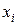
| 
| 
|
| 2,00 | -2,42 | 5,84 | |
| 2,50 | -1,92 | 3,67 | |
| 2,50 | -1,92 | 3,67 | |
| 3,00 | -1,42 | 2,01 | |
| 3,00 | -1,42 | 2,01 | |
| 4,00 | -0,42 | 0,17 | |
| 5,50 | 1,08 | 1,17 | |
| 5,50 | 1,08 | 1,17 | |
| 5,50 | 1,08 | 1,17 | |
| 6,00 | 1,58 | 2,51 | |
| 6,50 | 2,08 | 4,34 | |
| 7,00 | 2,58 | 6,67 | |
| Итого | 53,00 | 0,00 | 34,42 |
| В среднем | 4,4167 |
Рассчитаем дисперсию:

Рассчитаем стандартное отклонение:

Рассчитаем коэффициент вариации:

5. Для расчета показателей асимметрии и эксцесса построим таблицу 11, в которой рассчитаем  ,
,  ,
, 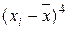
Таблица 11
| № | 
| 
| 
| 
|
| 2,00 | -2,42 | -14,11 | 34,11 | |
| 2,50 | -1,92 | -7,04 | 13,50 | |
| 2,50 | -1,92 | -7,04 | 13,50 | |
| 3,00 | -1,42 | -2,84 | 4,03 | |
| 3,00 | -1,42 | -2,84 | 4,03 | |
| 4,00 | -0,42 | -0,07 | 0,03 | |
| 5,50 | 1,08 | 1,27 | 1,38 | |
| 5,50 | 1,08 | 1,27 | 1,38 | |
| 5,50 | 1,08 | 1,27 | 1,38 | |
| 6,00 | 1,58 | 3,97 | 6,28 | |
| 6,50 | 2,08 | 9,04 | 18,84 | |
| 7,00 | 2,58 | 17,24 | 44,53 | |
| Итого | 53,00 | 0,00 | 0,11 | 142,98 |
| В среднем | 4,4167 |
Асимметрия распределения равна:
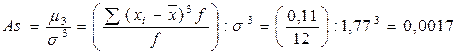
То есть, наблюдается левосторонняя асимметрия, так как  , что подтверждается и при расчете по формуле:
, что подтверждается и при расчете по формуле: 

В этом случае  , что для данной формулы так же указывает на левостороннюю асимметрию
, что для данной формулы так же указывает на левостороннюю асимметрию
Эксцесс распределения равен:

В нашем случае эксцесс отрицательный, то есть наблюдается плосковершинность.
Пример 6. По хозяйству представлены данные о заработной плате работников (табл. 12)
Рассчитать моду и медиану.
Решение.
Для интервального вариационного ряда мода рассчитывается по формуле:

где модальный интервал – интервал с наибольшей частотой, в нашем случае 3600-3800, с частотой 
 - минимальная граница модального интервала (3600);
- минимальная граница модального интервала (3600);
 - величина модального интервала (200);
- величина модального интервала (200);
 - частота интервала предшествующая модальному интервалу (25);
- частота интервала предшествующая модальному интервалу (25);
 - частота следующего за модальным интервалом (29);
- частота следующего за модальным интервалом (29);
 - частота модального интервала (68).
- частота модального интервала (68).
Таблица 12
Интервал по заработной плате, руб./чел.
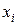
| Количество работников

| Кумулятивная частота |
| 3000-3200 | ||
| 3200-3400 | ||
| 3400-3600 | ||
| 3600-3800 | ||
| 3800-4000 | ||
| Итого | - |
Для интервального вариационного ряда медиана рассчитывается по формуле:

где медианный интервал это интервал, кумулятивная (накопленная) частота которого равна или превышает половину суммы частот, в нашем примере это 3600-3800.
 - минимальная граница медианного интервала (3600);
- минимальная граница медианного интервала (3600);
 - величина медианного интервала (200);
- величина медианного интервала (200);
 - сумма частот ряда (154);
- сумма частот ряда (154);
 - сумма накопленных частот, всех интервалов, предшествующих медианному (57);
- сумма накопленных частот, всех интервалов, предшествующих медианному (57);
 – частота медианного интервала (125).
– частота медианного интервала (125).
Пример 7. По трем хозяйствам одного района имеются сведения о фондоемкости продукции (количество затрат основных фондов на 1руб. произведенной продукции): I – 1,29 руб., II – 1,32 руб., III – 1,27руб. Необходимо рассчитать среднюю фондоемкость.
Решение. Так как фондоемкость обратный показатель оборота капитала используем формулу среднюю гармоническую простую.

Пример 8. По трем хозяйствам одного района имеются данные о валовом сборе зерновых  и средней урожайности (табл. 13).
и средней урожайности (табл. 13).
Таблица 13
| Хозяйство | Валовой сбор ц.

| Урожайность ц/га.

|
| I | ||
| II | ||
| III |
Необходимо рассчитать среднюю урожайность по хозяйствам.
Решение. Расчет средней урожайности по средней арифметической невозможен, так как отсутствуют сведения о количестве посевных площадей  , поэтому используем формулу средней гармонической взвешенной:
, поэтому используем формулу средней гармонической взвешенной:

Пример 9.Имеются данные о средней урожайности картофеля на отдельных участках и количестве окучиваний (табл. 14)
Таблица 14
| № участка | число окучиваний | урожайность ц./га | № | число окучиваний | урожайность ц./га | |
Проведем группировку данных (табл. 15):
Таблица 15
Группировка участков по признаку «число прополок»
| Количество прополок | Число участков | Урожайность, ц./га. | Групповая средняя 
|
| 63, 68, 69, 65, 67 | 66,4 | ||
| 72, 74, 70, 74, 68, 72, 73 | 71,8571 |
1. Рассчитаем общую дисперсию выборки (табл. 16):
Таблица 16
| № | Урожайность, ц./га 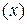
| 
| 
|
| -6,58333 | 43,3402 | ||
| -1,58333 | 2,5069 | ||
| 2,41667 | 5,8403 | ||
| 4,41667 | 19,5070 | ||
| 0,41667 | 0,1736 | ||
| -0,58333 | 0,3403 | ||
| -4,58333 | 21,0069 | ||
| -1,58333 | 2,5069 | ||
| 4,41667 | 19,5070 | ||
| -2,58333 | 6,6736 | ||
| 2,41667 | 5,8403 | ||
| 3,41667 | 11,6736 | ||
| В среднем | 69,58333 | ||
| Итого | 0,00000 | 138,9167 |

2. Рассчитаем дисперсию для каждой группы:
I. Группа с числом окучиваний - 1(табл. 17)
Таблица 17
| № | Урожайность, ц./га.  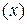
| 
| 
|
| -3,40 | 11,56 | ||
| 1,60 | 2,56 | ||
| 2,60 | 6,76 | ||
| -1,40 | 1,96 | ||
| 0,60 | 0,36 | ||
| В среднем | 66,4 | ||
| Итого | 23,20 |

II. Группа с числом окучиваний равным 2 (табл. 18)
Таблица 18.
| № | Урожайность, ц./га.  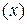
| 
| 
|
| 0,1429 | 0,02 | ||
| 2,1429 | 4,59 | ||
| -1,8571 | 3,45 | ||
| 2,1429 | 4,59 | ||
| -3,8571 | 14,88 | ||
| 0,1429 | 0,02 | ||
| 1,1429 | 1,31 | ||
| В среднем | 71,8571 | ||
| Итого | 28,86 |

3. Рассчитаем среднюю внутригрупповую дисперсию:
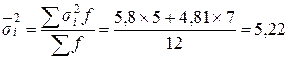 .
.
4. Найдем межгрупповую дисперсию. В соответствии с законом сложения дисперсии:
,  отсюда
отсюда

5. Рассчитаем корреляционное отношение:
 .
.
То есть, фактор, положенный в основу группировки (число окучиваний) оказывает среднее влияние на результат (урожайность).
| <== предыдущая лекция | | | следующая лекция ==> |
| Та компенсаційних виплат | | | ОСНОВНІ ПРИНЦИПИ ОРГАНІЗАЦІЇ ЗАРОБІТНОЇ ПЛАТИ |