News 56

Дата добавления: 2015-08-30; просмотров: 562

1. Факторы должны быть количественно соизмеримы. Качественные показатели переводят в количественную форму, например, выражая их в баллах.

2. Факторы, включаемые в модель множественной регрессии, не должны быть:

· интеркоррелированны – теснота связи между какими-то факторами больше, чем теснота связи между данными факторами и результативным признаком (например, ).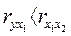

· коллинеарные – считается, что две переменные коллинеарные (находятся в линейной зависимости), если 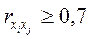, и тем более мультиколлинеарные – более чем два фактора находятся в линейной зависимости.

Значимость уравнения регрессии оценивается при помощи критерия Фишера (F-критерия).

В данном случае, при существенности уравнения регрессии, критерий Фишера фактический (берется из результатов, полученных при компьютерном расчете или рассчитывается самостоятельно) должен быть больше теоретического F-критерия (берется из таблицы «Значение критерия Фишера-Снедекора»).

Фактический F-критерий для уравнения парной регрессии в целом рассчитывается как:

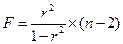, (10.21)

Оценку существенности уравнения регрессии проводят, сравнивая полученное значение F-критерия ( 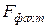) с табличным значением ( 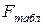), которое берут из таблиц критических значений F-отношений при определенном уровне значимост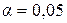и или 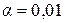, и числе свободы: 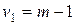, 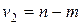(таблицы Снедекора-Фишера – приложение 2).

Фактический F-критерий для уравнения множественной регрессии в целом рассчитывается как:

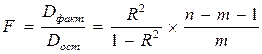, (10.22)

где 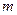- число параметров при переменных x;

n - число наблюдений;

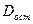- остаточная сумма квадратов на одну степень свободы;

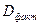- факторная сумма квадратов на одну степень свободы;

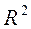- коэффициент (индекс) множественной детерминации.

Частный F-критерий для фактора 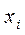определяется как:

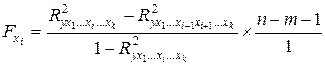, (10.23)

Если 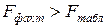то уравнение регрессии значимо, если меньше незначимо.

Значимость параметров уравнения 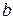и коэффициента корреляции 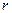парной модели проверяют при помощи критерия Стьюдента – .

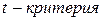Для парной линейной модели.

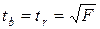, (10.24)

Полученные фактические значения критерия Стьюдента сравнивают с табличными значениями при определенном уровне значимост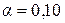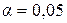и , или 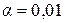, и числе степеней свободы 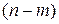(приложение 1), где - число единиц наблюдения, 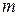- число параметров уравнения регрессии.

Значимость коэффициентов регрессии и корреляции множественной модели регрессии оценивается при помощи критерия Стьюдента ( 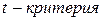). В данном случае, при существенности коэффициентов регрессии, критерий Стьюдента фактический (берется из результатов, полученных при компьютерном расчете или рассчитывается самостоятельно) должен быть больше теоретического 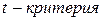(берется из таблиц 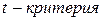Стьюдента при уровне значимости 0,10, 0,05, 0,01).

Фактический 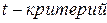для коэффициента регрессии при i-м факторе рассчитывается как:

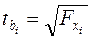, (10.25)

Фактический 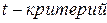для коэффициентов корреляции рассчитывается как:

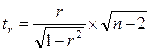, (10.26)

Если фактическое значение 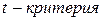больше табличного соответствующий коэффициент статистически значим.

Пример 24.Имеются данные о величине средней урожайности зерновых ц./га. и затратах на минеральные удобрения руб./на 1га. пашни по хозяйствам района (табл. 38).

Необходимо:

1. Рассчитать коэффициент парной линейной корреляции, парной линейной детерминации, сделать выводы по каждому коэффициенту.

2. Построить уравнение парной линейной регрессии, спрогнозировать 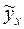при различных значениях фактора, то есть рассчитать:

· максимально возможную величину ;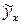

· минимальную ;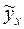

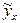· для средних значений фактора.

3. Провести статистическую оценку:

· уравнения регрессии;

· параметров уравнения регрессии и коэффициент корреляции.

Таблица 38

№	Исходные данные	Расчетные данные
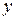
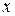
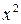
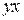
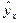
А
	9,49			635,83	10,93
	7,57			401,21	8,53
	9,95			696,50	11,45
	9,23			470,73	8,18
	11,97			718,20	9,73
	8,56			479,36	9,04
	11,18			503,10	7,15
	7,93			452,01	9,21
	15,75			1401,75	14,71
	13,61			1007,14	12,14
	2,99			164,45	8,87
	12,57			1093,59	14,37
	10,93			710,45	10,59
	9,86			532,44	8,70
	7,39			354,72	7,67
	9,23			563,03	9,90
	15,4			1216,60	13,00
	13,14			1116,90	14,03
	12,12			981,72	13,34
	10,27			657,28	10,42
	9,12			501,60	8,87
	13,42			966,24	11,79
	10,29			710,01	11,28
	14,55			1193,10	13,51
	15,26			1327,62	14,37
Итого	271,7800			18855,58	х
В среднем	10,87	66,64	х	754,22	х
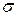
	2,9261	13,1602	х	х	х

Решение.

1. Рассчитаем коэффициент парной линейной корреляции:

,

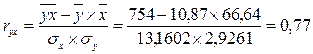Коэффициент парной линейной корреляции показывает, что затраты на минеральное уравнение оказывают сильное влияние на величину урожайности зерновых.

Коэффициент парной линейной детерминации рассчитывается как квадрат коэффициента парной линейной корреляции;

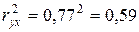
Показывает, что 59% всей вариации результативного признака обусловлено включенным в модель фактором.

2. Уравнение парной линейной регрессии имеет вид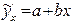

При расчете параметров уравнения при помощи МНК необходимо решить систему из двух нормальных уравнений.

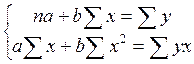
Рассчитаем все возможные значения в таблицу 38 и подставим в систему;

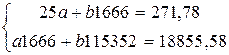
Разделим первое уравнение на 25, а второе на 1666

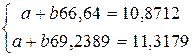
Вычтем из второго уравнение первое

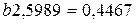
Отсюда

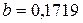
Подставим в первое уравнение систему 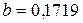и рассчитаем :

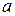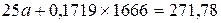
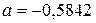
Получили уравнение парной линейной регрессии:

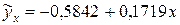
Параметр 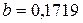, называется коэффициентом регрессии. В примере он показывает, что при увеличении затрат на минеральные удобрения на 1руб./га. пашни средняя урожайность зерновых, в среднем, возрастет на 0,1719ц/га.

Подставляя в уравнение значение фактора 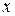рассчитаем 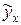табл.38.

Рассчитаем максимально возможную величину 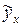. Коэффициент регрессии 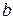положителен, поэтому возьмем максимальное значение фактора 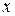(при отрицательном значении 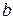берем минимальное значение фактора ).

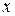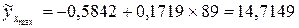
Рассчитаем минимально возможную величину 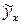. Коэффициент регрессии 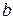положителен, поэтому возьмем минимальное значение фактора 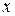(при отрицательном значении 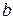берем максимальное значение фактора ).

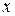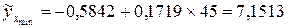
Рассчитаем величину 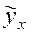при средних значениях фактора .

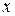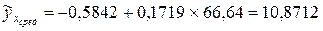
3. Проведем статистическую оценку уравнения регрессии его параметров и коэффициента корреляции.

Статистическую значимость уравнения регрессии определяют при помощи критерия Фишера ( ).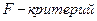

Рассчитаем фактическое значения критерия Фишера:

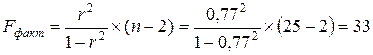
Теоретическое значение берем таблицы 5%-го уровня распределения F (приложение 3) .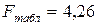

Так как 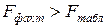, уравнение регрессии признается статистически значимым.

Статистическую значимость параметра 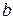и коэффициента корреляции 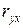определяют при помощи критерия Стьюдента ( ).

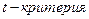Для парной линейной модели фактическое значения .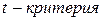

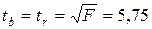
Табличное значение 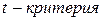берем из таблицы «Значение критерия t Стьюдента при уровне значимости 0,10, 0,05 и 0,01» (приложение 2) .

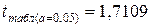Так как, фактические значения критерия Стьюдента больше табличных коэффициент регрессии и корреляции следует признать статистически значимым.

Общие положения по выполнения контрольной работы

Задание для контрольной работы согласовывается с преподавателем, ему же по выполнении она представляется для проверки. По результатам преподаватель выставляет оценку (зачет), или количество заработанных балов.