The Scope of Parental Rights and Duties

Дата добавления: 2015-08-30; просмотров: 612

Определение. Линейной функцией называется функция, которую можно задать формулой у = х + в, где и в – некоторые действительные числа, х и у – переменные.

Свойства функции:

1. Область определения:

2. Множество значений:

3. Линейная функция:

если в = 0 (функция имеет вид у = кх) нечетная f (-x) =- f(x);

если к = 0 (функция имеет вид у = в) – четная;

если в ≠ 0, к ≠ 0 – ни четная, ни нечетная.

4. Линейная функция:

если к = 0 – постоянная (у = в);

если к > 0 – возрастающая;

если к < 0 – убывающая.

Доказательство:

Возьмем два значения аргумента х₁ и х₂ из области определения функции такие, что х₁ < х₂, тогда х₂ - х₁ > 0 и запишем соответствующие им значения функции:

у₁ = кх₁ + в и у₂ = кх₂ + в.

Сравним у₁ и у₂ : у₂ – у₁ = (кх₂ + в) – (кх₁ + в) = к(х₂ - х₁)

Поскольку по условию х₂ - х₁> 0, то знак разности у₂ – у₁ зависит от знака к.

Если к > 0, то у₂ – у₁ > 0, значит у₂ > у₁, поэтому согласно определения возрастающей функции, линейная функция возрастающая на всем множестве действительных чисел R.

Если К < 0, то у₂ – у₁ < 0, значит у₂ < у₁, поэтому согласно определения убывающей функции, линейная функция убывающая на всем множестве действительных чисел R.

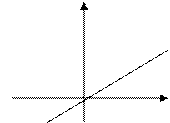
5. Графиком линейной функции является прямая:

	К > 0	К = 0	К < 0
в > 0
в = 0
в < 0