
Головна сторінка Випадкова сторінка
КАТЕГОРІЇ:
АвтомобіліБіологіяБудівництвоВідпочинок і туризмГеографіяДім і садЕкологіяЕкономікаЕлектронікаІноземні мовиІнформатикаІншеІсторіяКультураЛітератураМатематикаМедицинаМеталлургіяМеханікаОсвітаОхорона праціПедагогікаПолітикаПравоПсихологіяРелігіяСоціологіяСпортФізикаФілософіяФінансиХімія
Визначення помилки засобом середнього.
Дата добавления: 2015-09-15; просмотров: 765
|
|
Состояние окружающей среды и окружающая обстановка могут усиливать или ослаблять опасность поражения электротоком в электроустановках. Так, сырость, токопроводящая пыль, едкие пары и газы, разрушающе действуют на изоляцию и создают условия перехода напряжения на металлические нетоковедущие части оборудования (корпусы, станины, ограждения, металлические ручки и т. п.), к которым может прикасаться человек в ходе работы.
В зависимости от тех или иных условий, повышающих опасность воздействия тока на человека, разным помещениям присуща разная степень опасности поражения током - одним большая, другим - меньшая.
Согласно Правил устройства электроустановок (ПУЭ) помещения делятся по степени опасности поражения электротоком на три группы (см. рис. 8):
- помещения без повышенной опасности;
- помещения с повышенной опасностью;
- особо опасные помещения.

Рисунок 8 - Классификация помещений по степени опасности поражения электротоком
Помещения без повышенной опасности не содержат ни одного из признаков повышенной или особой опасности.
Помещения с повышенной опасностью характеризуются наличием одного из условий, создающих повышенную опасность:
- сырости или токопроводящей пыли. Сырыми считаются помещения, в которых относительная влажность воздуха длительно превышает 75% (потолок и стены не покрыты влагой). Токопроводящей пылью считается пыль, способная оседать на проводах и проникать вовнутрь машин и аппаратов. Различают помещения с токопроводящей пылью (графитная, угольная, металлическая и др.) и нетокопроводящей пылью (пыль абразивных материалов, древесная, цементная и др.). В пыльных помещениях по условиям производства выделяется технологическая пыль, способная оседать на проводах и проникать вовнутрь машин и аппаратов. Различают помещения с токопроводящей пылью (графитная, угольная, металлическая и др.) и нетокопроводящей пылью (пыль абразивных материалов, древесная, цементная и др.);
- токопроводящих полов (металлические, земляные, железобетонные, кирпичные и т. д.);
- высокой температуры. Это помещения, в которых температура воздуха длительно (более 1 сут.) превышает 35  С.
С.
- возможности одновременного прикосновения человека к соединенным с землей металлоконструкциям зданий, технологическим аппаратам, механизмам и т. д., с одной стороны, и к металлическим корпусам электрооборудования - с другой.
Особо опасные помещения характеризуются наличием хотя бы одного из условий, создающих особую опасность:
- особой сырости. В особо сырых помещениях относительная влажность воздуха близка к 100% (потолок, стены, пол и предметы покрыты влагой);
- химически активной или органической среды. Это помещения с длительным содержанием агрессивных паров, газов, отложений и плесени, разрушающих изоляцию и токоведущие части электрооборудования.
- одновременно двух и более признаков повышенной опасности.
Приведенная классификация лежит в основе мер, применяемых в защитных целях. Так например, в помещениях «без повышенной опасности» требуется применение мер защиты от косвенного прикосновения при переменном напряжении более 50 В, а при постоянном напряжении - более 120 В (защитное заземление, автоматическое отключение питания, уравнивание потенциалов, защитное разделение сетей ). А в помещениях «с повышенной опасностью» и в «особо опасных» помещениях эти меры требуются уже при переменном напряжении 25 В (при постоянном напряжении 60 В). А в отдельных случаях, по требованиям ПУЭ и отдельных нормативов, – при переменном напряжении 12 В и постоянном 30 В.
Важным условием электробезопасности является строгое соблюдение паспортных требований по эксплуатации электрооборудования, в которых обычно указываются группы помещения.
ВСТУП
Наш світ влаштований набагато складніше чим можемо собі уявити. Але не дивлячись на це, навіть той потік інформації, яка людина може сприйняти і обробити за певну одиницю часу, неймовірно великий. Чого тільки коштує одна графіка? Що говорити про окремі випадки, коли цей потік збільшується (гіпноз, медитація, магічна дія на навколишній світ).
Але це в ідеалі. Сліпа людина позбавлена графічного потоку, паралізований — позбавлений дотикової інформації, і так далі. Тобто, в принципі, інтелект може функціонувати в замкнутому просторі, не реагуючи на зовнішні чинники. І для цього вже не потрібна та обчислювальна потужність, якої потребує здорова людина. Для створення її вже достатньо обчислювальної потужності сучасних комп’ютерів. Але необхідна особлива структура оперативної пам’яті, відмінна від ємнісної.
Що є, звична для користувача комп’ютера, оперативна пам’ять? Це мікросхеми, чіпи, побудовані із ємнісних комірок. Кожна комірка має свою адресу (координати). Заповнена комірка – заряджена ємність (1), порожня, – розряджена (0). На обробку кожної комірки, запис, стирання, зчитування процесор виділяє окремі цикли. Тобто так він (комп’ютер) і працює: зчитує, рахує, записує результат.
А чи так само працює думка (людська оперативна пам’ять)? Адже не так! Людина не виділяє для її обслуговування циклів. Поява, зміна і знищення інформації в ній, звичайно, пов’язана з часом. Але обчислювальна потужність процесора, тобто робота мозку, направлена на обробку зовнішніх дій, і пошук інформації в статичній пам’яті при цьому проблем із ресурсами не має. Одиниці в нашій оперативній пам’яті не піддаються обчислювальному процесу. Вони видозмінюються під впливом зовнішніх чинників безпосередньо, «проїхала червона машина», «заболіла спина», «треба відповісти на лист від друга». У машинному коді ці думки займають різний бітовий простір пам’яті. У людському – один блок. У такому ж блоковому вигляді вони зберігаються в статичній пам’яті. Різний рівень інтелектуальних здібностей у людей, мабуть, пов’язаний з розмірами цього блока. Більше, блок – легше осмислення великого масиву інформації, швидший пошук в збереженій пам’яті [1].
Всі вже, напевно, чули про електромеханічних собак в Японії, які можуть впізнавати господаря в обличчя, виконувати деякі прості команди і мають деяку здібність до навчання. Чули і про холодильники з виходом в Інтернет і про впровадження Microsoft в майбутні версії Windows елементів штучного інтелекту.
У подібному розвитку області штучного інтелекту немає нічого незвичайного. Тут доречно привести гіпотезу про зустрічну еволюцію людини і комп’ютера: людина спочатку вчиться бачити, ходити, розмовляти, а вже потім розвиває здібності до обчислень і логічних висновків. Комп’ютер же навпаки, народжується як обчислювальна система, що базується на формальній логіці, в процесі розвитку набуває здібностей до розпізнавання образів, синтезу мови і управління в реальному часі [2].
В наш час розрізняють два основні підходи до моделювання штучного інтелекту (AI – artificial intelligence): машинний інтелект, який полягає в строгому завданні результату функціонування, і штучний розум, направлений на моделювання внутрішньої структури системи. Розділення робіт зі штучного інтелекту на два напрями пов’язане з існуванням двох точок зору на питання, яким чином будувати системи штучного інтелекту.
Свою нішу в системах штучного інтелекту займають екстремальні задачі комбінаторного типу, які об’єднують широке коло задач дискретної оптимізації. До цих задач відносяться задачі теорії розкладів, календарного планування, цілочисельного програмування, задачі про комівояжера та інші [1].
Дані задачі мають багато практичних застосувань, наприклад, при проектуванні інформаційних систем та обчислювальних комплексів, у задачах маршрутизації в системах масового обслуговування та комп’ютерних мережах. У цьому плані найбільший інтерес представляє відома “задача комівояжера”, суть якої полягає в знаходженні найкоротшого замкнутого шляху обходу вершин графа (міст, станів певної системи і т. п.), які задані своїми координатами [2].
Відомо, що задачі такого типу в загальному випадку мають багато екстремальний характер і є NP-повними [1, 2]. Наприклад, при розв’язанні задачі комівояжера, як правило, використовуються лише наближені алгоритми розв’язання. Вони мають достатньо високу швидкодію та поліноміальну часову складність, але дають лише наближені до точних результати. Точні методи типу простого перебору, гілок та границь дозволяють ефективно розв’язувати такі задачі, але мають експоненціальну складність, що не дозволяє використовувати їх для задач великої розмірності.
Сучасний підхід до розв’язання такого класу задач пов’язують з використанням методів штучного інтелекту — нейроподібних мереж та еволюційних алгоритмів випадково-детермінованого пошуку, серед яких найбільш поширеними є генетичні [3]. Відомо, що такі структури моделюють роботу кори мозку людини та еволюційний процес розвитку живої природи, мають можливість паралельної обробки даних, і, за рахунок цього, забезпечують суттєвий виграш часу при розв’язанні задач великої розмірності.
У даному курсовому проекті ставиться завдання розв’язання задачі комівояжера за допомогою генетичного алгоритму.
Таким чином, предметом дослідження є генетичний алгоритм за допомогою якого буде розв'язуватися поставлена задача.
Об’єктом дослідження в даному курсовому проекті є генетичні процеси, які нагадують біологічну еволюцію та інтерпретуються як складові компоненти алгоритму під час програмування.
Метою курсового проекту є розв’язання задачі комівояжера за допомогою генетичного алгоритму.
АНАЛІЗ ПРЕДМЕТНОЇ ОБЛАСТІ
Слід зауважити, що існує ряд простих методів розв'язання задачі комівояжера: повний лексичний перебір, жадібні алгоритми(метод найближчого сусіда), метод включення найближчого міста, метод найдешевшого включення, метод мінімального кістяка дерева. На практиці застосовують різні модифікації ефективніших методів, серед яких:метод гілок і меж, метод генетичних алгоритмів, а також алгоритм мурашиної колонії.
Всі ефективні (такі, що скорочують повний перебір) методи розв'язання задачі комівояжера — евристичні. У більшості евристичних методів знаходиться не найефективніший маршрут, а наближений розв'язок.
Задача комівояжера (комівояжер — подорожуючий торговець; англ. Travelling Salesman Problem, TSP; нім. Problemdes Handlungsreisenden) полягає у знаходженні найвигіднішого маршруту, що проходить через вказані міста хоча б по одному разу. В умовах завдання вказуються критерій вигідності маршруту (найкоротший, найдешевший, сукупний критерій тощо) і відповідні матриці відстаней, вартості тощо. Зазвичай задано, що маршрут повинен проходити через кожне місто тільки один раз, в такому випадку розв'язок знаходиться серед гамільтонових циклів.
Невідомо, коли проблему комівояжера було досліджено вперше. Однак, відома книжка, що видана в 1832 році з назвою “Комівояжер — як він має поводитись і що має робити для того, аби доставляти товар та мати успіх в своїх справах — поради старого Кур'єра», в якій описано проблему, але математичний апарат для її розв'язання не застосовується. Натомість, в ній запропоновано приклади маршрутів для деяких регіонів Німеччини та Швейцарії [4].
Генетичні алгоритми в різних формах застосовуються до вирішення багатьох наукових і технічних проблем. Генетичні алгоритми використовуються при створенні інших обчислювальних структур, наприклад, автоматів або мереж сортування. У машинному навчанні вони використовуються при проектуванні нейронних мереж або керуванні роботами. Вони також застосовуються при моделюванні розвитку в різних предметних областях, включаючи біологічні (екологія, імунологія і популяційна генетика) та соціальні (такі як економіка і політичні) системи.
Проте, можливо, найбільш популярне застосування генетичних алгоритмів - оптимізація багато параметричних функцій. Багато реальних задач можуть бути сформульовані як пошук оптимального значення, де значення - складна функція, що залежить від певних вхідних параметрів. У деяких випадках, потрібно знайти ті значення параметрів, при яких досягається найкраще точне значення функції. В інших випадках, коли точний оптимум не потрібний - рішенням може вважатися будь-яке значення, краще за певну задану величину. У цьому випадку, генетичні алгоритми - часто найбільш прийнятний метод для пошуку "прийнятних" значень. Сила генетичного алгоритму полягає в його здатності маніпулювати одночасно багатьма параметрами, що використовується в сотнях прикладних програм, включаючи проектування літаків, налаштування параметрів алгоритмів і пошуку стійких станів систем нелінійних диференціальних рівнянь [5].
Генетичні алгоритми є ефективною процедурою пошуку, що конкурує з іншими процедурами. Ефективність генетичних алгоритмів значно залежить від таких деталей, як метод кодування рішень, операторів, налаштування параметрів, окремих критеріїв успіху. Теоретична робота, подана в літературі, присвяченої генетичним алгоритмам, не дає підстав говорити про вироблення певних строгих механізмів для чітких передбачень.
1.1 Основні поняття теорії графів для задачі комівояжера
Нехай G – неорієнтований граф. Геометрично граф можна представити як набір вершин (точок), певні пари яких з'єднані лініями. Наприклад, мережа доріг, що з'єднують міста Е1, Е2, Е3, Е4, Е5, можна представити у вигляді графа таким чином. Міста позначені крапками (вершинами), а дороги - неорієнтованими лініями (рис. 1.1).

Рисунок 1.1 – Неорієнтований граф
Неорієнтовані лінії означають наявність двостороннього руху між відповідною парою міст. Перетин ліній не вважається вершиною. При зображенні графа не має значення розташування вершин на площині, кривизна і довжина ребер (рис. 1.2).
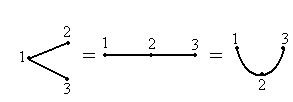
Рисунок 1.2 – Властивість зображення графа
Вершини графів позначаються буквами або натуральними числами. Ребра графа – пари чисел. Графічні представлення - наочні відображення досліджуваної системи чи процесу явища на площині: малюнки, креслення, схеми і блок-схеми, діаграми, графи. На мові теорії графів формуються і вирішуються багато технічних завдань, завдання з області економіки, соціології, менеджменту і т.д. Графи використовуються для наочного представлення об'єктів і зв'язків між ними.
Маршрутом G називається така кінцева або нескінченна послідовність ребер, в якій кожні два сусідніх ребра мають кінцеву точку.
Циклічним маршрутом називається такий маршрут, початкова та кінцева точки якого збігаються.
Ланцюгом називають маршрут, в якому кожне його ребро зустрічається не більше одного разу; вершини в ланцюзі можуть повторюватися не більше одного разу. Будь-яка ділянка ланцюга є ланцюгом. Нециклічні ланцюги є простими ланцюгами, якщо в них ніяка вершина не повторюється.
Граф називається зв'язним, якщо між парою його вершин існує така послідовність елементів (дуг або ребер, або ж і дуг, і ребер), що будь-які сусідні елементи в цій послідовності мають загальну вершину. Очевидно, що будь-який сильно зв'язний граф є зв'язним. Зв'язний неорієнтований граф називається деревом, якщо він не має циклів. У дереві будь-які дві вершини зв'язані єдиним ланцюгом [6].
1.2 Формулювання і деякі властивості рішень задачі комівояжера
Комівояжер (подорожуючий торговець) повинен вийти з першого міста, відвідати по разу в невідомому порядку міста 2, 1, 3 .. n і повернутися в перше місто. Відстані між містами відомі.
У якому порядку слід обходити міста, щоб замкнутий шлях (тур) комівояжера був найкоротшим?
Щоб привести завдання до наукового формулювання, введемо деякі терміни. Міста пронумеровані числами jÎТ=(1,2,3..n). Тур комівояжера може бути описаний циклічною перестановкою t = (j1, j2, ..,jn, j1), слід зауважити, що всі j1..jn - різні номера міст; повторюваний на початку і в кінці j1, показує, що перестановка зациклена. Відстані між парами вершин Сij утворюють матрицю С.
Завдання полягає в тому, щоб знайти такий тур t:
| (1.1) |
 .
.
Щодо математичного формулювання задачі комівояжера доречно зробити декілька зауважень.
1) У постановці Сij означали відстані, тому вони повинні бути невід'ємними, тобто для всіх jÎТ [6]:
Сij³0; Cjj=∞. (1.2)
Остання рівність означає заборону петель в турі, тобто для всіх i, j:
Сij=Сji (1.3)
і задовольняти нерівність трикутника, тобто для всіх:
Сij+Сjk³Cik. (1.4)
У математичній постановці йдеться про довільну матрицю. Зроблено це тому, що існує багато прикладних задач, які описуються основною моделлю, але всі умови (1.2) – (1.4) не задовольняють. Особливо часто порушується умова (1.3) (наприклад, якщо Сij - не відстань, а плата за проїзд: часто в одну сторону квиток коштує певну ціну, а назад - інакшу). Тому будемо розрізняти два варіанти задачі комівояжера: симетричну задачу, коли умова (1.3) виконується, і несиметричну - в іншому випадку. Умови (1.2) – (1.4) за замовчуванням будемо вважати такими що виконуються.
2) У несиметричній задачі комівояжера всі тури t = (j1, j2, .., jn, j1) і t '= (j1, jn, .., j2, j1) мають різну довжину і повинні враховуватися обидва. Різних турів очевидно (n-1)! [6].
Зафіксуємо на першому та останньому місці в циклічній перестановці номер j1, а номера, що залишилися, їх кількість рівна n-1 переставимо усіма (n-1)! можливими способами. В результаті отримаємо всі несиметричні тури. Симетричних турів буде у два рази менше, тому що кожен зарахований двічі: як t і як t'. Можна представити, що С складається тільки з одиниць і нулів. Тоді С можна інтерпретувати, як граф, де проведено ребро (i, j), якщо Сij = 0 і ребро відсутнє, якщо Сij = 1. Таким чином, якщо існує тур довжиною 0, то він пройде по циклу, який включає всі вершини по одному разу. Такий цикл носить назву гамільтонового циклу. Незамкнутий гамільтонів цикл називається гамільтоновим ланцюгом (гамільтонів шлях).
У термінах теорії графів симетричну задачу комівояжера можна сформулювати так: “Дано повну мережу з n вершинами, довжина ребра (i, j) = Сij. Знайти гамільтонів цикл мінімальної довжини. У несиметричній задачі про комівояжера замість “цикл” слід вживати слово “контур”, а замість “ребра”–“дуги” або “стрілки”.
Деякі прикладні задачі формулюються як задачі про комівояжера, але в них потрібно мінімізувати довжину не гамільтонового циклу, а гамільтонового ланцюга. Такі задачі називаються незамкненими. Деякі моделі зводяться до задачі про декілька комівояжерів, але тут їх розглядати не будемо.
1.3 Постановка задачі комівояжера як завдання на графі
Формулювання задачі. Є деяка множина міст А={a1,…,ai,…,an}. Відстань між містами i та j – ρ(аi, aj). П – множина перестановок елементів А, перестановка, отже
 , (1.5)
, (1.5)
де
 ,
,  . (1.6)
. (1.6)
Якщо містам поставити у відповідність вершини графа, а дорогам що їх з’єднують – дуги, то в термінах теорії графів задача полягає у визначенні гамільтонового контуру мінімальної довжини (рис. 1.3).
Гамільтоновим контуром називається шлях, що проходить через усі вершини графа, у якого початкова вершина збігається з кінцевою. Тут під довжиною контуру розуміють не кількість дуг, що входять в контур, а суму їх довжин. Довжина відповідної дороги - вага ребра. Граф повинен бути повним, тобто в ньому повинні бути всі можливі ребра. Якщо ж граф не є повним, то його можна доповнити відсутніми ребрами з вагою рівною ∞ [6].

Рисунок 1.3 – Графічна інтерпретація розв’язку задачі комівояжера
1.4 Аналіз даних для задачі комівояжера
Перш за все проаналізуємо основні дані (вхідні та вихідні), які будуть використовуватись при подальшому розв’язанні задачі комівояжера.
Вхідні дані:
- кількість міст, які розглядаються при розв’язанні задачі;
- вартість шляху між кожними двома містами, які мають між собою сполучення;
- кількість ітерацій на протязі яких буде здійснюватись пошук оптимального шляху.
Щодо кількості міст, які повинні розглядатися при розв’язанні поставленої задачі, то тут слід зауважити, що генетичний алгоритм, який буде застосований при розв’язані задачі про комівояжера найбільш ефективний коли кількість міст, які повинен відвідати комівояжер перевищує, принаймні, 100. Проте в даному курсовому проекті будемо розглядати варіанти задач в яких дана кількість становить кілька десятків – цей фактор зумовлений певними програмними обмеженнями, які будуть зауважені в наступних розділах.
Вартість шляху між кожними двома містами, які мають між собою сполучення будемо задавати довільно цілими числами з певного інтервалу числової прямої.
Кількість ітерацій – один із основних показників, який характеризує точність остаточного результату. Загальновідома істина: “Чим більша кількість ітерацій – тим вища ефективність”. Тобто якщо кількість ітерацій буде прямувати до безкінечності – то похибка результату буде прямувати до нуля. В курсовому проекті обмежимось кількома сотнями ітерацій, що ефективно для декількох десятків міст.
Вихідні дані:
- вартість оптимального шляху;
- оптимальний шлях.
Оптимальний шлях – це деяка впорядкована множина міст, вартість шляху між якими найменша серед усіх розглянутих алгоритмом маршрутів, що обмежені показником ітерацій.
Вартість оптимального шляху – це числовий показник, який враховує сумарну вартість шляху між містами, які пройде комівояжер обходячи найефективніший маршрут.
Таким чином, пошук розв’язку задачі про комівояжера в курсовому проектуванні здійснюється при використанні генетичного алгоритму, що повністю відповідає темі курсового проекту. Слід зауважити про ефективність даного алгоритму для розв’язання задач такого типу [5]. Саме за допомогою генетичного алгоритму в повній мірі буде знайдено ефективний розв’язок задачі, який не завжди можна знайти за допомогою стандартних алгоритмів, які використовуються під час розв’язання задачі про комівояжера. Серед таких методів є: метод гілок та меж [4], метод оціночної функції [2] та інші.
| <== предыдущая лекция | | | следующая лекция ==> |
| Методи апаратного та програмного захисту інформації. Антивірусне програмне забезпечення. Програмне забезпечення для стиску та архівації файлів даних. | | | Зауваження. |