ХІД ВИКОНАННЯ РОБОТИ

Дата добавления: 2015-09-15; просмотров: 702

Задача дисконтирования формулируется следующим образом: требуется определить начальную сумму А₀ через время t по её конечной величине A(t) при процентной ставке p.

Пусть A(t) – конечная сумма, полученная за t лет, А₀ – начальная сумма. Если проценты простые, то в конце каждого года t сумма A(t) в сбербанке по сравнению с прошлым годом (t - 1) увеличивается на p % от начальной суммы А₀:

A(t) = A(t- 1) + 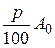, или A(t) = .

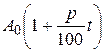Откуда дисконтированная сумма вычисляется по формуле:

.

При начислении сложных процентов конечная сумма вычисляется по формуле

A(t) = ,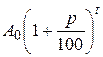

откуда дисконтированная (начальная) сумма к моменту времени t:

.

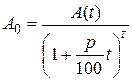При непрерывном начислении процентов конечная сумма вычисляется по формуле

A(t) = ,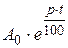

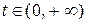
откуда дисконтированная сумма к моменту времени t: .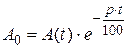

Если предположить, что деньги вкладываются в банк постоянно, образуя денежный поток, который выражается непрерывной функцией А₀(t). Тогда общую сумму 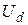, вложенную в банк за период времени [0, T], можно вычислить по формуле

,

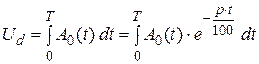где A(t) – ежегодно поступающий доход.

Величина 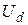(Т) называется дисконтной суммой (от английского discount - скидка) за период времени [0, T].

Контрольные вопросы:

1. В чем заключается экономический смысл определённого интеграла?

2. Что называется коэффициентом Джини? Как он рассчитывается?

3. В чем заключается задача дисконтирования?

Литература:

1. Высшая математика для экономистов: Учебник для вузов / Н.Ш. Кремер, Б.А. Путко, И.М. Тришин, М.Н.Фридман. Под ред. Н.Ш. Кремера. – М.: ЮНИТИ, 2005. – 471 с.

2. Общий курс высшей математики для экономистов: Учебник. / Под ред. В.И. Ермакова. –М.: ИНФРА-М, 2006. – 655 с.

3. Сборник задач по высшей математике для экономистов: Учебное пособие / Под ред.В.И. Ермакова. М.: ИНФРА-М, 2006. – 574 с.

4. Данко П.Е., Попов А.Г., Кожевникова Т.Я. Высшая математика в упражнениях и задачах. Ч. 1, 2. – М.: Оникс 21 век: Мир и образование, 2005. – 304 с. Ч. 1; – 416 с. Ч. 2.

5. Математика в экономике: Учебник: В 2-х ч. / А.С. Солодовников, В.А. Бабайцев, А.В. Браилов, И.Г. Шандара. – М.: Финансы и статистика, 2006.

6. Шипачев В.С. Высшая математика: Учебник для студ. вузов – М.: Высшая школа, 2007. – 479 с.