Графічне розв’язування нерівностей та систем нерівностей.

Дата добавления: 2015-09-15; просмотров: 848

б) статистическое оценивание неизвестных параметров модели

в) формулировка вида модели, состава и формы входящих в нее связей

г) сбор необходимой статистической информации

д) статистическое оценивание неизвестных параметров модели

59. Укажите условие для наблюдаемого значения критерия Дарбина-Уотсона, при котором, автокорреляция остатков считается положительной

А)

Б)

В)

Г)

Д)

Тема 4 Модель множественной линейной регрессии

60. На основании рядов данных для переменных X и Y построено уравнение регрессии: . Какое из следующих высказываний является верным:

а) Оценка коэффициента β=1,25 означает, что если значение переменной Х увеличится в среднем на 1,25, то значение переменной Y при прочих равных условиях увеличится на 1 единицу.

б) Оценка коэффициента β=1,25 означает, что если значение переменной Y увеличится на 1 единицу, то значение переменной X при прочих равных условиях увеличится в среднем на 1,25.

в) Форма уравнения регрессии показывает, что переменные Х и Y линейно зависят друг от друга.

г) Если при прочих равных условиях значение переменной Х удвоится, то значение переменной Y возрастет в среднем на 25%.

д) Константа в уравнении регрессии равна 1,25

61. Эластичность показывает:

а) На сколько единиц изменится фактор x_k при изменении результирующего показателя y на 1 единицу.

б) На сколько единиц изменится результирующий показатель y при изменении фактора x_k на 1 единицу.

в) На сколько % изменится фактор x_k при изменении результирующего показателя y на 1 % .

г) На сколько % изменится результирующий показатель y при изменении фактора x_k на 1 %.

д) Меру реакции одного фактора при неизменном состоянии другого.

62. Пусть Y — товарооборот магазина, млн. тенге, Х₁ — торговая площадь, тыс.кв.м, Х₂ — среднее количество посетителей в день, тыс. чел.

Каков будет товарооборот магазина, если он находится в относительно оживленном месте с количеством посетителей 20000 и имеет торговую площадь 1000 кв. м?

а) 8242,168 млн. тенге

б) 8,243 млн. тенге

в) 7,411 млн. тенге

г) 3,911 млн. тенге

д) 4,743 млн. Тенге

63. Число степеней свободы при расчете t-статистики в случае множественной регрессии равно:

а) n, где n – число наблюдений

б) k, где k - количество независимых переменных Х

в) n – k

г) n – (k + 1)

д) n – (k + 2)

64. Достоинства рассчитанной линии парной регрессии нельзя оценить с помощью:

а) оценки статистической значимости коэффициентов регрессии по t-критерию Стьюдента

б) дисперсионного анализа и F-критерия Фишера

в) построения доверительных интервалов коэффициентов регрессии

г) проверки существенности выборочного коэффициента корреляции

д) теста Вальда

65. Оценки â и ,полученные МНК, являются:

а) несмещенными и неэффективными

б) смещенными и неэффективными

в) несмещенными и эффективными

г) смещенными и эффективными

д) несмещенными

66. При расчете F-статистики для парной регрессии число степеней свобода k₁ равно:

а) 0

б) 1

в) 2

г) 3

д) 4

67. При расчете F-статистики для парной регрессии число степеней свобода k₂ равно:

а) 0

б)1

в) n-1

г) n-2

д) n-3

68. О значимости уравнения парной регрессии свидетельствует значение вероятности (probability) при F-статистике:

а) равное 1

б) меньше 1

в) больше 0

г) меньше 0,05

д) меньше 0,5

69. Высокое значение линейного коэффициента корреляции свидетельствует о:

а) Y является причиной Х

б) Х является причиной Y

в) Х не является причиной Y

г) Х и Y тесно связаны

д) Х и Y не связаны

70. Коэффициент уравнения регрессии показывает

а) На сколько % изменится результат при изменении фактора на 1 %.

б) На сколько % изменится фактор при изменении результата на 1 %.

в) На сколько единиц изменится результат при изменении фактора на 1 единицу.

г) На сколько единиц изменится фактор при изменении результата на 1 единицу.

д) Во сколько раз изменится результат при изменении фактора на 1 единицу.

71. Стандартизованный коэффициент уравнения a_к^s применяется

а) При проверке статистической значимости k-го фактора.

б) При проверке экономической значимости k-го фактора.

в) При отборе факторов в модель.

г) При проверке на гомоскедастичность.

д) При проверке важности фактора по сравнению с остальными факторами

72. Стандартизированные коэффициенты регрессии показывают:

а) стандартную ошибку

б) стандартное отклонение

в) на сколько σ изменится в среднем Y при изменении Х_j на одну σ при неизменном среднем уровне других Х

г) наиболее типичные коэффициенты для данного уравнения множественной регрессии

д) наличие гетероскедастичности

73. Парная регрессия представляет собой модель вида:

а) y=f(x)+ε

б) y=f(x₁,x₂,…x_к) +ε

в) y=f(y _t-1) +ε

г) y=f(y _t+1) +ε

д) y=f(x²) +ε

74. Величина коэффициента регрессии показывает:

а) среднее изменение Y с изменением X на одну единицу

б) среднее изменение Y с изменением X на один процент

в) изменение Y в процентах с изменением X на один процент

г) изменение Y в процентах в результате среднего изменения X

д) среднее изменение Х

75. Суть МНК состоит в:

а) минимизации суммы квадратов коэффициентов регрессии

б) минимизации суммы квадратов значений зависимой переменной

в) минимизации суммы квадратов отклонений точек наблюдений от уравнения регрессии

г) минимизации суммы квадратов отклонений точек эмпирического уравнения регрессии от точек теоретического уравнения регрессии

д) минимизации суммы квадратов значений независимой переменной

76. Чему равно количество степеней свободы для множественной линейной регрессии y=f(x1,x2,x3) с 20 наблюдениями?

А) 18;

Б) 16;

В) 19;

Г) 22;

Д) 20.
77. Коэффициент эластичности показывает:

а) на сколько единиц изменится фактор при изменении результата на 1 единицу

б) на сколько единиц изменится результат при изменении фактора на 1 единицу

в) во сколько раз изменится результат при изменении фактора на одну единицу

г) на сколько % изменится результат при изменении фактора на 1 %

д) на сколько %изменится фактор при изменении результата на 1%

78. Не является предпосылкой классической модели предположение:

а) факторы экзогенны

б) длина исходного ряда данных больше, чем количество факторов

в) матрица факторов содержит все важные факторы, влияющие на результат

г) регрессоры являются случайными величинами

д) математическое ожидание ошибки равно нулю

79. На основании наблюдений за 100 домохозяйствами построено эмпирическое уравнение регрессии У=145,65+0,825*х, где у-потребление, х –доход. Коэффициент равен:

а) 145,65

б) 0,825

в) 146,475

г) 144,825

д) 1

Тема 5 Классическая модель множественной линейной регрессии.

80. Классический подход к оцениванию коэффициентов регрессии основан на:

а) графической оценке

б) методе максимального правдоподобия

в) методе наименьших квадратов

г) методе моментов

д) аналитическом методе

81. Гипотеза о значимости коэффициента регрессии принимается, если рассчитанное значение t-статистики:

а) больше табличного значения t-статистики

б) меньше табличного значения t-статистики

в) равно табличному значению t-статистики

г) больше 0

д) меньше 0

82. Критерий Фишера показывает

а) Долю изменчивости зависимой переменной, объясненную влиянием факторов, включенных в модель.

б) Тесноту связи между фактическими и расчетными значениями результирующего показателя.

в) Статистическую значимость модели в целом на основе совокупной достоверности всех ее коэффициентов.

г) Экономическую значимость модели в целом.

д) Статистическую значимость коэффициентов регрессии.

83. Табличное значение критерия Фишера зависит

а) Только от уровня доверительной вероятности.

б) Только от числа факторов, включенных в модель.

в) Только от длины исходного ряда.

г) Только от уровня доверительной вероятности и числа факторов, включенных в модель.

д) От числа факторов, включенных в модель и от длины исходного ряда.

84.Модель в целом статистически значима, если:

а) F_расч. < F_табл .

б) ç F_расч. ç< F_табл .

в) F_расч. > F_табл .

г) F_расч. = F_табл .

д) F_расч≠F_табл .

85. При расчете t-статистики для коэффициентов парной регрессии число степеней свободы принимается равным:

а) 0

б) 1

в) n (n – число наблюдений)

г) n – 1 (n – число наблюдений)

д) n – 2 (n – число наблюдений)

86. В классической линейной модели множественной регрессии принимаются следующие основные гипотезы:

а) Е (u_i) ≠ 0

б) Е (u_i, u_j) ≠

в) Х₁, Х₂, …, Х_k –случайные переменные

г) Е (u_i) = 0

д) Е (u_i) = 1

87. МНК-оценки β_j, полученные для классической линейной модели множественной регрессии являются:

а) несмещенными и неэффективными

б) смещенными и неэффективными

в) несмещенными и эффективными

г) смещенными и эффективными

д) несмещенными

88. Коэффициент детерминации R²:

а) равен 0

б) лежит в интервале [0; 1]

в) лежит в интервале [-1; 0]

г) равен 1

д) лежит в интервале [-1; 1]

89. Дисперсионный анализ применяется для расчета:

а) F-критерия Фишера

б) t-статистики

в) R²

г) скорректированного R²

д) коэффициента корреляции

90. Число степеней свободы k₁ при расчете F-критерия для случая множественной регрессии равно:

а) n, где n – число наблюдений

б) k, где k - количество независимых переменных Х

в) n – k

г) n – (k + 1)

д) n – (k + 2)

91. Уравнение множественной регрессии значимо, если рассчитанное значение F-критерия:

а) больше 0

б) больше 1

в) больше F-табличного

г) равен F-табличному

д) меньше F-табличного

92. Критерий Стьюдента предназначен для:

а) Определения экономической значимости каждого коэффициента уравнения

б) Определения статистической значимости каждого коэффициента уравнения

в) Проверки модели на автокорреляцию остатков

г) Определения экономической значимости модели в целом

д) Проверки на гомоскедастичность

93. Если коэффициент уравнения регрессии (b_k) статистически значим, то:

а) b_k > 1.

б)|b_k | > 1.

в) b_k ¹ 0

г) b_k > 0

д) 0 < b_k < 1.

94. Критерий Фишера предназначен для:

а) Определения экономической значимости каждого коэффициента уравнения

б) Определения статистической значимости каждого коэффициента уравнения

в) Проверки модели на автокорреляцию остатков

г) Определения статистической значимости модели в целом

д) Проверки на гомоскедастичность

95. Зависимость между коэффициентами множественной детерминации (R²) и корреляции (r) описывается следующей формулой:

а) R² = 1–r².

б) R²=1–r.

в) r= .

г) R²= .

д) R² = 1+r².

96. Корреляционная зависимость между текущими уровнями некоторой переменной и уровнями этой же переменной, сдвинутыми на несколько периодов времени назад называется:

А) гомоскедастичность

Б) мультиколлинеарностъ

В) автокорреляция

Г) гетероскедастичность;

Д) коллинеарность.
97. Что минимизируется согласно методу наименьших квадратов:

а)

б)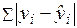

в)

г)

д)

98 Графический метод подбора вида уравнения регрессии основан на:

а) изучении дисперсии остатков

б) изучении коэффициента корреляции

в) сравнении величины остаточной дисперсии при разных моделях

г) изучении поля корреляции

д) изучении априорной информации об экономической сущности анализируемой зависимости

99. Найдите предположение, не являющееся предпосылкой классической модели.

а) Случайное отклонение имеет нулевое математическое ожидание

б) Случайное отклонение имеет постоянную дисперсию

в) Отсутствует автокорреляция случайных отклонений

г) Случайное отклонение независимо от объясняющих переменных

д) Случайное отклонение не обладает нормальным распределением

100. По результатам бюджетного обследования пяти семей записано следующее уравнение регрессии накоплений (регрессоры – доход и имущество, тыс. тенге) y=0,279+0,123x₁-0,029 x_2. Спрогнозируйте накопление семьи, имеющей доход 40 тыс. тенге и имущество стоимостью 25 тыс. тенге:

а) 4,474

б) 3,78

в) 5,06

г) 5,47

д) 5,24

101. Модель вида Y_i = β₀ + β₁X_1i + β₂X_2i + u_i, i = 1, …, n служит примером:

а) парной регрессии

б) множественной регрессии

в) простой регрессии

г) временного ряда

д) истинной модели

102. В уравнении множественной регрессии y = 2,35 + 15Х₁ + 3Х₂ + 34Х₃ коэффициент β₀ равен:

а) 0

б) 2,35

в) 3

г) 15

д) 34

103. В уравнении множественной регрессии y = 20 + 5Х₁ + 25Х₂ + 4Х₃ коэффициент β₁ равен:

а) 0

б) 20

в) 5

г) 25

д) 4

104. В уравнении множественной регрессии y = 50 + 1,05Х₁ + 17,2Х₂ + 34Х₃ коэффициент β₂ равен:

а) 0

б) 50

в) 1,05

г) 17,2

д) 34

105. В уравнении множественной регрессии y = 500 + 105Х₁ + 25Х₂ + 0,34Х₃ коэффициент β₃ равен:

а) 0

б) 500

в) 105

г) 25

д) 0,34

106. В уравнении множественной регрессии y = 5 + 105Х₁ + 25Х₂ + 34Х₃ константа равна:

а) 0

б) 5

в) 105

г) 25

д) 34

107. Число включаемых переменных Х₁, …, Х_k в модель множественной регрессии должно быть:

а) равно числу наблюдений

б) меньше числа наблюдений

в) больше числа наблюдений

г) больше числа наблюдений в 2-3 раза

д) меньше числа наблюдений в 5-6 раз

Тема 6 Коэффициент детерминации

108. Коэффициент детерминации характеризует:

а) соотношение факторной и остаточной дисперсий

б) долю остаточной дисперсии в общей дисперсии Y

в) долю остаточной дисперсии

г) долю дисперсии Х в общей дисперсии Y

д) дисперсию Y

109. Коэффициент детерминации может принимать значение:

а) положительное

б) отрицательное

в) нулевое

г) в интервале [-1; 1]

д) в интервале [0; 1]

110. Для определения доли дисперсии Y, объясненной линейной зависимостью от Х, используют:

а) t-статистику

б) F-статистику

в) дисперсионный анализ

г) коэффициент детерминации

д) коэффициент корреляции

111. Число степеней свободы k₂ при расчете F-критерия для случая множественной регрессии равно:

а) n, где n – число наблюдений

б) k, где k - количество независимых переменных Х

в) n – k

г) n – (k + 1)

д) n – (k + 2)

112. Коэффициенты множественной регрессии значимо отличаются от нуля, если:

а) t-статистика больше t-табличного

б) t-статистика меньше t-табличного

в) t-статистика равно t-табличного

г) t-статистика больше F-критерия

д) t-статистика меньше F-критерия

113. Для расчета совместного влияния факторов Х₁, …, Х_k на результат (Y) используется:

а) коэффициент парной корреляции

б) коэффициент частной корреляции

в) как парной, так и частной корреляции

г) множественный коэффициент корреляции

д) коэффициент детерминации

114. Коэффициент детерминации R² свидетельствует о:

а) размере стандартной ошибки

б) размере стандартного отклонения

в) качестве регрессионной модели

г) эффективности оценок коэффициентов

д) неэффективности оценок коэффициентов

115. Суть коэффициента детерминации 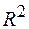состоит в следующем:

а) коэффициент определяет долю общего разброса значений 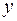, объясненного уравнением регрессии

б) коэффициент свидетельствует о значимости коэффициентов регрессии

в) коэффициент определяет тесноту связи между признаками

г) коэффициент свидетельствует о наличии автокорреляции

д) коэффициент свидетельствует об отсутствии автокорреляции

116. Добавление новой объясняющей переменной:

а) уменьшает значение коэффициента детерминации до нуля

б) редко уменьшает значение коэффициента детерминации

в) никогда не уменьшает значение коэффициента детерминации

г) иногда уменьшает значение коэффициента детерминации

д) не оказывает влияния на значение коэффициента детерминации

117. Укажите верное утверждение о скорректированном коэффициенте детерминации:

а) скорректированный коэффициент детерминации меньше или равен обычному коэффициенту детерминации для к>1

б) скорректированный коэффициент детерминации больше обычного коэффициента детерминации для к>1

в) скорректированный коэффициент детерминации равен обычному коэффициенту детерминации для к>1

г) скорректированный коэффициент детерминации меньше обычного коэффициента детерминации для к>1

д) скорректированный коэффициент детерминации равен 0 для к>1

118. Уравнение множественной регрессии является качественным, если:

а) коэффициент детерминации меньше 0,8

б) t-статистики, F-статистика, DW-статистика высокие

в) t-статистики, F-статистика, DW-статистика низкие

г) t-статистики, F-статистика больше критических значений, предпосылки МНК соблюдены

д) F-статистика больше критического значения

119. Множественный коэффициент корреляции используется для проверки наличия в модели:

а) автокорреляции остатков

б) гетероскедастичности

в) мультиколлинеарности

г) линейной зависимости между зависимой и независимой переменными

д) фиктивной переменной

120. Когда целесообразно добавление новой объясняющей переменной в модель?

а) при росте R²

б) если в модели мало переменных

в) в любом случае

г) если модель не соответствует экономической теории

д) при росте скорректированного R²

121. В уравнении множественной регрессии y = 5.3 + 13Х₁ + 0,2Х₂ + 3Х₃ коэффициент β₀ равен:

а) 5.3

б) 13

в) 0,2

г) 3

д) 0

122. В уравнении множественной регрессии y = 225 + 0.5Х₁ + 0,2Х₂ + 3Х₃ коэффициент β₁ равен:

а) 225

б) 0.5

в) 0,2

г) 3

д) 0

123. В уравнении множественной регрессии y = 225 + 13Х₁ + 0,2Х₂ + 0.3Х₃ коэффициент β3 равен:

а) 225

б) 13

в) 0,2

г) 0.3

д) 0

Тема 7 Спецификация переменных. Частная корреляция.

124. Выбор формы связи между переменными называется:

а) идентифицируемостью

б) верификацией

в) спецификацией

г) индентификацией

д) информатизацией

125. В случае если пропущены важные переменные в модели, оценки коэффициентов регрессии:

а) смещенные, но обладают меньшей дисперсией

б) смещенные, но обладают большей дисперсией

в) несмещенные, но обладают меньшей дисперсией

г) несмещенные, но обладают большей дисперсией

д) неэффективные

126. В случае если включены «лишние» переменные в модель регрессии оценки коэффициентов регрессии:

а) смещенные, но обладают меньшей дисперсией

б) смещенные, но обладают большей дисперсией

в) несмещенные, но обладают меньшей дисперсией

г) несмещенные, но обладают большей дисперсией

д) неэффективные

127. Для расчета «чистой» корреляции между двумя переменными в классической линейной модели множественной регрессии используется коэффициент:

а) парной корреляции

б) частной корреляции

в) как парной, так и частной корреляции

г) множественной корреляции

д) детерминации

128. Использование парной регрессии вместо множественной регрессии является примером ошибки:

а) выборки

б) спецификации

в) измерения

г) стандартной

д) нестандартной

129. Автокорреляция остатков – это:

а) зависимость между значениями случайных ошибок

б) непостоянство дисперсии случайной ошибки

в) постоянство дисперсии случайной ошибки

г) отклонения коэффициентов регрессии от среднего значения

д) сильная взаимосвязь между регрессорами

130. Применение обыкновенного МНК к модели с автокорреляцией остатков приведет к следующим последствиям:

а) выборочные дисперсии оценок коэффициентов будут неэффективными

б) стандартные ошибки коэффициентов будут оценены неправильно

в) прогнозы по модели эффективные

г) прогнозы по модели неэффективные

д) выборочные дисперсии оценок коэффициентов будут неэффективными, стандартные ошибки коэффициентов будут оценены неправильно, прогнозы по модели неэффективные

131. Простейшим способом проверки наличия автокорреляции является:

а) графическое изображение остатков

б) тест Уайта

в) теста Бреуша-Пагана

г) тест Гольдфельда-Куандта

д) критерий однородности дисперсии Бартлетта

132. Для проверки существования автокорреляции используется:

а) t-статистика

б) критерий Дарбина-Уотсона

в) тест Уайта

г) тест Гольдфельда-Куандта

д) F-статистика

133. Критерий знаков используется для проверки наличия в модели:

а) автокорреляции остатков

б) гетероскедастичности

в) мультиколлинеарности

г) линейной зависимости между зависимой и независимой переменными

д) фиктивной переменной

134. Критерий Дарбина-Уотсона используется для проверки наличия в модели:

а) автокорреляции остатков

б) гетероскедастичности

в) мультиколлинеарности

г) линейной зависимости между зависимой и независимой переменными

д) фиктивной переменной

135. При проверке нулевой гипотезы о гомоскедастичности с помощью тесты Уайта, она будет отвергнута, если Probability (вероятность) меньше:

а) 0,04

б) 0,05

в) 0,06

г) 0,07

д) 0,08

136. Для оценки однородности двух разных выборок данных используется:

а) тест Уайльда

б) тест Уайта

в) тест Гольфреда-Куандта

г) тест Чоу

д) тест Дарбина-Уотсона

137. Включение в совокупность единиц с “выбросами” данных является примером ошибки:

а) выборки

б) спецификации

в) измерения

г) стандартной

д) нестандартной

138. Заниженная балансовая прибыль в отчетности является примером ошибки:

а) выборки

б) спецификации

в) измерения

г) стандартной

д) нестандартной

Тема 8 Нелинейные эконометрические модели

139. Система одновременных уравнений – это:

а) система взаимозависимых уравнений

б) система независимых уравнений

в) приведенная форма модели

г) система взаимозависимых уравнений или структурная форма модели

д) два взаимосвязанных уравнения

140. Внешние факторы, не поддающиеся учету и регистрации, воздействующие на временные ряды, называются:

а) циклическими

б) случайными

в) неслучайными

г) сезонными

д) долговременными

141. Факторы, формирующие в длительной перспективе общую тенденцию анализируемого признака, называются:

а) циклическими

б) случайными

в) неслучайными

г) сезонными

д) долговременными

142. Если при выборе функции тренда примерно одинаковы цепные абсолютные приросты Δ_t (первые разности уровней ряда), то следует выбрать:

а) линейную функцию

б) параболу второго порядка

в) экспоненту

г) гиперболу

д) полином

143. Если при выборе функции тренда примерно одинаковы абсолютные ускорения уровней ряда Δ_Δ (вторые разности ряда), то следует выбрать:

а) линейную функцию

б) параболу второго порядка

в) экспоненту

г) гиперболу

д) полином

144. Если при выборе функции тренда примерно одинаковы цепные коэффициенты роста k_t, то следует выбрать:

а) линейную функцию

б) параболу второго порядка

в) экспоненту

г) гиперболу

д) полином

145. Для определения порядка аппроксимирующего полинома используется:

а) метод последовательных разностей членов временного ряда

б) метод расчета цепных абсолютных приростов

в) метод расчета абсолютных ускорений уровней ряда

г) метод расчета цепных коэффициентов роста

д) метод наименьших квадратов

146. Модель авторегрессии порядка 1 описывают:

а) стационарные ряды

б) нестационарные ряды

в) случайные ряды

г) неслучайные ряды

д) сезонные ряды

147. Если значение t-статистики, рассчитанное для коэффициента регрессии, больше по модулю критического (табличного значения), это означает, что коэффициент:

а) верный

б) неверный

в) значимый

г) незначимый

д) наилучший

148 Одновременное формирование спроса Q^d и предложения Q^s товара в зависимости от его цены служит примером:

а) парной регрессии

б) множественной регрессии

в) временных рядов

г) системы одновременных уравнений

д) эконометрической модели

149. Суть МНК состоит в:

а) Минимизации суммы квадратов коэффициентов регрессии

б) Минимизации суммы квадратов значений зависимой переменной

в) Минимизации суммы квадратов отклонений точек наблюдений от уравнения регрессии

г) Минимизации суммы квадратов отклонений точек эмпирического уравнения регрессии от точек теоретического уравнения регрессии.

д) Минимизации дисперсии случайного члена.

150. Идентификация уравнения эконометрической модели – это:

а) статистическое оценивание неизвестных параметров модели

б) формулировка вида модели, состава и формы входящих в нее связей

в) сбор необходимой статистической информации

г) статистическое оценивание неизвестных параметров модели

д) проверка точности модельных данных

151. Аналитический метод подбора вида уравнения регрессии основан на:

а) изучении дисперсии остатков

б) изучении коэффициента корреляции

в) сравнении величины остаточной дисперсии при разных моделях

г) изучении поля корреляции

д) изучении априорной информации об экономической сущности анализируемой зависимости

152. Оценка значимости уравнения регрессии в целом дается с помощью:

а) коэффициента детерминации

б) F-критерия Фишера

в) стандартной ошибки регрессии

г) коэффициента корреляции

д) критерия Стьюдента

153. Если фактор не оказывает влияния на результат, то линия регрессии на графике:

а) параллельна оси оу

б) является биссектрисой первой четверти декартовой системы координат

в) параллельна оси ох

г) перпендикулярна оси ох

д) выпукла к началу координат

154. По выборке данных можно построить так называемое:

а) любое уравнение регрессии

б) теоретическое уравнение регрессии

в) значимое уравнение регрессии

г) незначимое уравнение регрессии

д) эмпирическое уравнение регрессии

Тема 9 Мультиколлинеарность

155. Мультиколлинеарность – это:

а) линейная взаимосвязь между Y и X

б) непостоянство дисперсии случайных отклонений

в) постоянство дисперсии случайных отклонений

г) взаимосвязь между случайными отклонениями

д) сильная линейная взаимосвязь двух или нескольких объясняющих переменных

156. Признаком мультиколлинеарности является:

а) высокое значение F-статистики

б) высокое значение статистики DW

в) высокое значение t-статистики

г) высокие коэффициент детерминации и частные коэффициенты корреляции

д) низкое значение статистики DW

157. Мультиколлинеарность – это:

а) сильная взаимосвязь между Y и Х_j, j = 1, …, k

б) сильная взаимосвязь между Х_j j = 1, …, k

в) сильная взаимосвязь между Y_i , i = 1, …, n

г) слабая взаимосвязь между Y и Х_j

д) слабая взаимосвязь между Х_j j = 1, …, k

158. Признаками мультиколлинеарности не являются:

а) большие стандартные ошибки коэффициентов регрессии

б) неправильные с точки зрения экономической теории знаки при коэффициентах регрессии

в) незначимость коэффициентов регрессии при значимости уравнения регрессии в целом

г) небольшие стандартные ошибки коэффициентов регрессии

д) большие коэффициенты корреляции между Х_j j = 1, …, k

159. К методам устранения мультиколлинеарности не относится:

а) удаление из модели одного или нескольких факторов

б) преобразование факторов, при котором уменьшается корреляция между ними

в) использование в модели ридж-регрессии

г) объединение факторов, при котором уменьшается корреляция между ними

д) корректировка гетероскедастичности остатков

160. F-критерий характеризует:

а) долю факторной дисперсии в общей дисперсии Y

б) соотношение факторной и остаточной дисперсий

в) долю факторной дисперсии в общей дисперсии X

г) долю остаточной дисперсии в общей дисперсии Y

д) дисперсию Х

161. Имеется уравнение, полученное МНК:

(2,14) (0,0034) (3,42) (0,009). В скобках указаны ошибки. Значимым является коэффициент:

а) β₁

б) β₂

в) β₃

г) β₁ и β₃

д) β₁ и β₂

162. Чем скорректированный R² отличается от обычного:

а) скорректированный R² не связан с обычным R²

б) скорректированный R²содержит поправку на число степеней свободы для получения несмещенных оценок дисперсии

в) скоректированный R² больше, чем обычный R²

г) скорректированный R² вычисляется намного проще, чем обычный R²

д) скоректированный R² равен обычному R²

163. По результатам бюджетного обследования пяти семей записано следующее уравнение регрессии накоплений (регрессоры – доход и имущество, тыс. тенге) y=0,279+0,123x₁-0,029x_2. Оцените, как возрастут накопления семьи, если ее доход вырос на 10 тыс. тенге, а стоимость имущества не изменилась?

а) 10,123

б) 10,0

в) 12,3

г) 0,123

д) 1,23

164. Какая программа используется при эконометрическом моделировании:

а) EViews

б) Power Point

в) Word

г) Power Point

д) Access.

165. С увеличением числа наблюдений n дисперсии оценок а и b:

а) не изменяются

б) увеличиваются

в) уменьшаются

г) становятся значимыми

д) становятся незначимыми

166. В результате увеличения объема выборки:

а) точность прогноза по модели не изменяется

б) увеличивается точность оценок

в) уменьшается коэффициент детерминации

г) уменьшается точность прогноза по модели

д) уменьшается точность оценок

167. Множественный коэффициент корреляции Rух₁x₂=0,8. Определите, какой процент дисперсии зависимой переменной у объясняется влиянием х₁ и x_2.

а) 64%

б) 80%

в) 28%

г) 32%

д) 20%

168. Какое значение не может принять множественный коэффициент корреляции:

а) 1

б) 1,2

в) 0

г) 0.5

д) 0,3

169. Коэффициент детерминации показывает

а) Долю изменчивости зависимой переменной, объясненную влиянием факторов, включенных в модель.

б) Тесноту связи между фактическими и расчетными значениями результирующего показателя в базисном периоде.

в) Статистическую значимость модели в целом на основе определения совокупной достоверности всех ее коэффициентов.

г) Экономическую значимость модели в целом.

д) Эконометрическую значимость модели в целом.

Тема 10 Гетероскедастичность

170. Гетероскедастичность – это:

а) непостоянство дисперсии случайной ошибки

б) постоянство дисперсии случайной ошибки

в) отклонения коэффициентов регрессии от среднего значения

г) большие стандартные ошибки коэффициентов регрессии

д) сильная взаимосвязь между регрессорами

171. Гомоскедастичность подразумевает:

а)

б)

в)

г) Х₁…Х_к - неслучайные переменные

д)

172. Тест Гольдфельда-Куандта используется для проверки наличия в модели:

а) автокорреляции остатков

б) гетероскедастичности

в) мультиколлинеарности

г) линейной зависимости между зависимой и независимой переменными

д) фиктивной переменной

173. Тест Уайта используется для проверки наличия в модели:

а) автокорреляции остатков

б) гетероскедастичности

в) мультиколлинеарности

г) линейной зависимости между зависимой и независимой переменными

д) фиктивной переменной

174. Критерий однородности дисперсии Барлетта используется для проверки наличия в модели:

а) автокорреляции остатков

б) гетероскедастичности

в) мультиколлинеарности

г) линейной зависимости между зависимой и независимой переменными

д) фиктивной переменной

175. Укажите тест, используемый для оценки гетероскедастичности:

А) Фишера;

Б) Дарбина-Уотсона;

В) Стьюдента;

Г) Пирсона;

Д) Гольдфельда-Квандта.

176. Основное последствие гетероскедастичности:

а) неэффективные оценки МНК

б) небольшие стандартные ошибки коэффициентов регрессии

в) эффективные оценки МНК

г) небольшие дисперсии оценок

д) высокое значение F-статистики.

177. Для проверки выборки на гетероскедастичность не может быть использован тест:

а) критерия однородности дисперсии Бартлетта

б) Гольдфельда-Куандта

в) Уайта

г) Бреуша-Пагана

д) Вальда

178. Какое из утверждений верно применительно к гетероскедастичности:

а) оценки вследствие гетероскедастичности перестают быть состоятельными;

б) оценки и дисперсии оценок остаются несмещенными

в) выводы по статистикам являются ненадежными (применительно к гетероскедастичности)

г) гетероскедастичность проявляется через низкое значение статистики DW

д) гетероскедастичность не сказывается на статистиках

179. В чем суть гетероскедастичности:

а) случайные отклонения взаимно коррелированы

б) дисперсии случайных отклонений изменяются

в) дисперсии случайных отклонений постоянны

г) случайные отклонения равны для всех наблюдений

д) случайные отклонения некоррелированы

180. Какое из утверждений о гетероскедастичности не верно:

а) проблема гетероскедастичности обычно характерна для перекрестных данных

б) выводы по t –статистикам и F-статистике при гетероскедастичности являются ненадежными

в) не существует общего теста для анализа гетероскедастичности

г) гетероскедастичность проявляется через низкое значение статистики Дарбина – Уотсона

д) гетероскедастичность делает ненадежными статистические тесты

181. Для регрессии за период 1971-1998 гг. получены следующие результаты (для данных 1971-1980 гг.), ( для данных 1989-1998 гг.). Сделайте вывод о постоянстве дисперсии отклонений:

а) дисперсия отклонений непостоянна

б) дисперсия отклонений постоянна

в) дисперсия отклонений составляет 35

г) дисперсия отклонений не влияет на качество регрессии

д) дисперсия отклонений равна 65

182. Какие требования в линейной модели множественной регрессии предъявляются к математическому ожиданию и дисперсии случайных отклонений:

а)

б)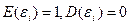

в)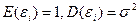

г)

д)

183. Для обнаружения автокорреляции применяют:

а) тест Глейзера

б) критерий DW

в) тест Голдфелда-Квандта

г) тест Спирмена

д) тест Уайта

184. Переменные, определяемые из уравнений модели, называются:

а) независимые

б) предопределенные

в) определенными

г) зависимые

д) стандартными

185. Переменные, задаваемые «из вне», в определенной степени управляемые (планируемые), называются:

а) экзогенные

б) эндогенные

в) предопределенные

г) лаговые

д) зависимые

186. Пространственные данные фиксируются:

а) по нескольким объектам за период времени

б) по одному объекту за период времени

в) в один и тот же момент времени по нескольким объектам

г) по одному объекту в определенный момент времени

д) по нескольким объектам , находящимся в некотором пространстве

Тема 11 Временные ряды в эконометрике

187. Временной ряд – это:

а) пространственные данные

б) выборка наблюдений разных объектов в один и тот же момент времени

в) последовательность наблюдений одного и того же объекта без учета моментов времени

г) упорядоченная во времени последовательность наблюдений

д) данные поперечного среза

188. Временной ряд, полученный в результате наблюдения одной характеристики исследуемого объекта, называется:

а) стационарным

б) дискретным

в) случайным

г) детерминированным

д) одномерным

189. Временной ряд с равноотстоящими моментами времени называется:

а) стационарным

б) дискретным

в) случайным

г) детерминированным

д) одномерным

190. Временной ряд, полученный как реализация случайной величины, называется:

а) стационарным

б) дискретным

в) случайным

г) детерминированным

д) одномерным

191. Ряд y(t) (t – момент времени) с дисперсией, ковариацией и средним, не зависящим от t, называется:

а) стационарным

б) дискретным

в) случайным

г) детерминированным

д) одномерным

192. Временной ряд, полученный как значение некоторой неслучайной функции, называется:

а) стационарным

б) дискретным

в) случайным

г) детерминированным

д) одномерным

193. Выберите характеристику наблюдений, соответствующую временным рядам:

а) порядок наблюдений несущественен

б) статистически независимы

в) количество наблюдений, как правило, большое

г) распределены одинаково

д) часто встречается автокорреляция

194. Факторы, формирующие периодически повторяемые в определенное время года колебания анализируемого признака, называются:

а) циклическими

б) случайными

в) неслучайными

г) сезонными

д) долговременными

195. Факторы, формирующие изменения анализируемого признака в результате воздействия циклов различной природы, называются:

а) циклическими

б) случайными

в) неслучайными

г) сезонными

д) долговременными

196. Уровень временного ряда может содержать:

а) тренд, циклические, сезонные колебания, случайные колебания

б) тренд и сезонные колебания

в) сезонные и случайные колебания

г) любое сочетание тренда, циклических, сезонных, случайных колебаний

д) циклические и сезонные колебания

197. Если коэффициент уравнения регрессии (β _k ) статистически значим, то

а) β _k > 1.

б) |β _k | > 1.

в) β _k ¹ 0.

г) β_k > 0.

д) 0 < β_k < 1.

198. Регрессионный анализ не является инструментом решения следующих основных задач:

а) построение для любых значений объясняющей переменной X наилучших по некоторому критерию оценок для неизвестной функции f(X)

б) построение по заданным критериям объясняющей переменной X наилучшего по некоторому критерию прогноза для неизвестной функции Y(X)

в) построение наилучшей оценки для неизвестного параметра θ, от которого зависит f(X, θ)

г) оценка удельного веса влияния каждой переменной X наY

д) определение теоретических экономических концепций

199. Эконометрическая модель описывает:

а) функциональные связи между переменными

б) стохастические связи между переменными

в) набор цифровых данных

г) состав переменных

д) статистические данные

200. Функция вида y(t)=T(t)+ξ_t, где t–время, T(t) – временной тренд заданного параметрического вида, ξ – случайная компонента является:

а) моделью тренда

б) моделью сезонности

в) регрессионной моделью с одним уравнением

г) моделью тренда и сезонности

д) моделью с одной переменной

201. Функция вида y(t)= S(t)+ξ_t, где t–время, S(t) – периодическая (сезонная) компонента, ξ – случайная компонента является:

а) моделью тренда

б) моделью сезонности

в) регрессионной моделью с одним уравнением

г) моделью тренда и сезонности

д) моделью с одной переменной

202. Функция вида y(t)=T(t)+S(t)+ξ_t, где t–время, T(t) – временной тренд заданного параметрического вида, S(t) – периодическая (сезонная) компонента, ξ – случайная компонента является:

а) моделью тренда

б) моделью сезонности

в) регрессионной моделью с одним уравнением

г) аддитивной моделью тренда и сезонности

д) мультипликативной моделью тренда и сезонности

203. Функция вида y(t)= T(t)S(t)+ξ_t, где t–время, T(t) – временной тренд заданного параметрического вида, S(t) – периодическая (сезонная) компонента, ξ – случайная компонента является:

а) моделью тренда

б) моделью сезонности

в) регрессионной моделью с одним уравнением

г) аддитивной моделью тренда и сезонности

д) мультипликативной моделью тренда и сезонности