Головна сторінка Випадкова сторінка
КАТЕГОРІЇ:
АвтомобіліБіологіяБудівництвоВідпочинок і туризмГеографіяДім і садЕкологіяЕкономікаЕлектронікаІноземні мовиІнформатикаІншеІсторіяКультураЛітератураМатематикаМедицинаМеталлургіяМеханікаОсвітаОхорона праціПедагогікаПолітикаПравоПсихологіяРелігіяСоціологіяСпортФізикаФілософіяФінансиХімія
Теоретичні відомості
Дата добавления: 2015-09-18; просмотров: 601
|
|
1.Изолирование и уточнения корня
Изолируем корни с помощью графического метода.
Для построения графика составляем таблицу для нескольких точек и строим график функции f(x)=x3-11x+4
| х | -5 | -4,5 | -4 | -3,5 | -3 | -2,5 | -2 | -1,5 | -1 | -0,5 | |
| у | -66 | -37,625 | -16 | -0,375 | 15,875 | 17,125 | 9,375 |
| х | 0,5 | 1,5 | 2,5 | 3,5 | 4,5 | |||||
| у | -1,375 | -6 | -9,125 | -10 | -7.875 | -2 | 8,375 | 45,625 |
Из данного графика видно, что интересующий нас корень уравнения принадлежит промежутку x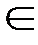 
[2,5;3,5]
По теореме Коши проверяем истинность корня:
f(2,5)=-7,875 f(3,5)=8,375 f(2,5)*f(3,5)<0
f '(x)=3x2-11
f '(2,5)=7,75–m1 f'(3,5)=25,75–M1 f'(2,5)*f'(3,5)>0
f "=6x
f "(2,5)=15 f"(3,5)=21 f"(2,5)* f"(3,5)>0
2. Решение уравнения
2.1 Метод простой итерации
М1=25,75 начальное приближение х0=2,5
хi=хi-1-f(xi-1)/M1 Для х1=2,5-(2,53-11*2,5+4)/25,75
| i | xi | xi-xi-1 |
| 2,5 | ||
| 2,805825 | 0,305825243 | |
| 2,991254 | 0,185428455 | |
| 3,074331 | 0,083077787 | |
| 3,103868 | 0,029536272 | |
| 3,113184 | 0,009316454 | |
| 3,115992 | 0,002808025 | |
| 3,116826 | 0,000834013 | |
| 3,117073 | 0,000246608 | |
| 3,117146 | 7,28224E-05 | |
| 3,117167 | 2,14957E-05 | |
| 3,117174 | 6,34438E-06 | |
| 3,117175 | 1,87245E-06 | |
| 3,117176 | 5,52622E-07 |
Решение с точностью ε=10-4 было достигнуто на 9 итерации, с точностью ε=10-6 на 13
α 
=1-7,75/25,75=0,699029
при 
Δх= 
=0,000169
при 
Δх= 
=1,28351E-06
х=3,117±0,0002 х=3,11717±1*10-6
2,2 Метод Ньютона
Условие f(x)*f "(x)<0, тогда х0=3,5
xi=хi-1-f(xi-1)/f'(xi-1) Для х1=3,5-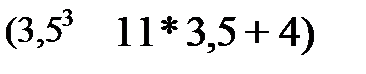 
/(6*3,52-11)
| i | xi | xi-xi-1 |
| 3,5 | ||
| 3,174757282 | 0,325242718 | |
| 3,118807783 | 0,055949499 | |
| 3,117177547 | 0,001630236 | |
| 3,117176177 | 1,36977E-06 | |
| 3,117176177 | 9,66338E-13 |
Решение с точностью ε=10-4 было достигнуто на 4 итерации, с точностью ε=10-6 на 5.
при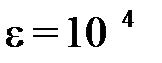 
Δх 
=2,26319E-12
при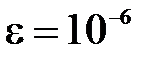 
Δх 
=0
x=3,117176177±2*10-12 x=3,117176177
2.3. Метод хорд
Условие f(x)*f"(x)>0, тогда х0=2,5 координата и значение функции в неподвижном конце промежутка 
=3,5; 
=8,375
Для х1=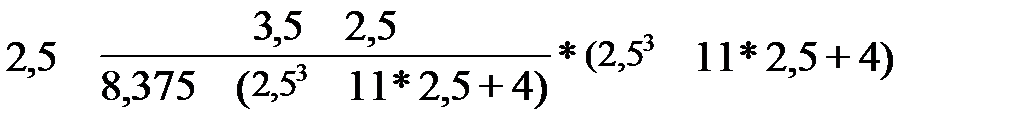 
| i | xi | xi-xi-1 |
| 2,5 | ||
| 2,984615385 | 0,484615385 | |
| 3,093527163 | 0,108911779 | |
| 3,113114926 | 0,019587763 | |
| 3,116483415 | 0,003368489 | |
| 3,117058143 | 0,000574728 | |
| 3,11715607 | 9,79271E-05 | |
| 3,117172752 | 1,66818E-05 | |
| 3,117175594 | 2,84163E-06 | |
| 3,117176078 | 4,84048E-07 |
Решение с точностью ε=10-4 было достигнуто на 6 итерации, с точностью ε=10-6 на 9
при 
Δх 
=4,70895E-05
при 
Δх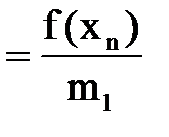 
=2,32751E-07
x=3,1172±5*10-5 x=3,117176±2*10-7
Вывод. Построение графика функции и расчеты производились в MS Excel.
В ходе выполнения данной практической работы ознакомились с итерационными методами численного решения нелинейных уравнений. Уяснили сущность задачи и метода её решения. Корни во всех методах получились одинаковы.
Наиболее точный метод – метод Ньютона,
метод простой итерации: 
Δх=2*10-4;
Δх=1*10-6
метод Ньютона Δх=2*10-12;
Δх=0
метод хорд Δх=5*10-5
Δх=2*10-7
| <== предыдущая лекция | | | следующая лекция ==> |
| Завдання на лабораторну роботу | | | Завдання на лабораторну роботу |