
Головна сторінка Випадкова сторінка
КАТЕГОРІЇ:
АвтомобіліБіологіяБудівництвоВідпочинок і туризмГеографіяДім і садЕкологіяЕкономікаЕлектронікаІноземні мовиІнформатикаІншеІсторіяКультураЛітератураМатематикаМедицинаМеталлургіяМеханікаОсвітаОхорона праціПедагогікаПолітикаПравоПсихологіяРелігіяСоціологіяСпортФізикаФілософіяФінансиХімія
ПРАКТИЧНА РОБОТА №3
Дата добавления: 2015-09-19; просмотров: 883
|
|
Перед тем, как решать игру m×n, нужно, прежде всего, попытаться ее упростить, избавившись от лишних стратегий. Это делается подобно тому, как мы когда-то отбрасывали заведомо невыгодные решения в §6. Введем понятие «доминирования». Стратегия Аi игрока А называется доминирующей над стратегией Ak, если в строке Аi стоят выигрыши не меньшие, чем в соответствующих клетках строки Ak, и из них по крайней мере один действительно больше, чем в соответствующей клетке строки Ak. Если все выигрыши строки Ai равны соответствующим выигрышам строки Ak то стратегия Аi называется дублирующей стратегию Ak. Аналогично определяются доминирование и дублирование для стратегий игрока В: доминирующей называется та его стратегия, при которой везде стоят выигрыши не большие, чем в соответствующих клетках другой, и по крайней мере один из них действительно меньше; дублирование означает полное повторение одного столбца другим. Естественно, что если для какой-то стратегии есть доминирующая, то эту стратегию можно отбросить; также отбрасываются и дублирующие стратегии.
Поясним сказанное примером. Пусть игра 5×5 задана матрицей таблицы 27.1.
Таблица 27.1

Прежде всего заметим, что в ней стратегия А5 дублирует стратегию А2, поэтому любую из них можно отбросить. Отбрасывая А5, замечаем, что в строке А1 все выигрыши больше (или равны) соответствующим выигрышам строки А4, значит А1 доминирует над A4. Отбросим А4 и получим матрицу 3×5 (таблица 27.2).
Но это еще не все! Приглядевшись к таблице 27.2, замечаем, что в ней некоторые стратегии игрока В доминируют над другими: например, B3 над B4 и B5, а В1 — над стратегией В2 (не забудьте, что В стремится отдать поменьше!). Отбрасывая столбцы В2, В4, В5, получаем игру 3×2 (таблица 27.3).
Наконец, в таблице 27.3 строка A3 дублирует A1 поэтому ее можно отбросить. Окончательно получим игру 2×2 (таблица 27.4).
Т а б л и ц а 27.2

 Таблица27.3 Таблица27.4
Таблица27.3 Таблица27.4
Эту игру, как ни старайся, уже не упростишь. Приходится решать. Попутно заметим, что, отбрасывая лишние (дублирующие и заведомо невыгодные) стратегии в игре с седловой точкой, мы придем к решению в чистых стратегиях. Но лучше сразу проверить, не обладает ли игра седловой точкой — это проще, чем сравнивать почленно все строки и все столбцы.
В руководствах по теории игр обычно останавливаются на решении простейших игр 2×2, 2 × п и т × 2, которое допускает геометрическую интерпретацию, но мы этого делать не будем — сразу возьмем «быка за рога» и покажем, как можно решить любую игру т × п.
Пусть имеется игра т × п без седловой точки с матрицей (aij) (см. таблицу 27.5).
Т а б л и ц а 27.5

Допустим, что все выигрыши aij положительны (этого всегда можно добиться, прибавляя ко всем членам матрицы достаточно большое число М; от этого
цена игры увеличится на M, а решение S*A, S*b не
изменится). Если все aij положительны, то конечно, и
цена игры, т. е. средний выигрыш при оптимальной
стратегии, тоже положителен: v > 0.
Мы хотим найти решение игры, т. е. две оптимальные смешанные стратегии
 (27.1)
(27.1)
дающие каждой стороне максимально возможный для
нее средний выигрыш (минимальный проигрыш).
Найдем сначала S*A. Мы знаем, что если один из
игроков (в данном случае это А) применяет свою оптимальную стратегию, то другой (В) не может улучшить свое цоложение, отступая от своей. Заставим противника (В) отступать от своей оптимальной стратегии, пользуясь чистыми стратегиями В1 В2,…, Вп
(а мы тем временем упорно держимся стратегии S*A).
В любом случае наш выигрыш будет не меньше, чем и:

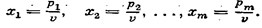 Разделим неравенства (27.2) на положительную величину v и введем обозначения:
Разделим неравенства (27.2) на положительную величину v и введем обозначения:
(27.3)
Тогда условия (27.2) примут вид:

(27.4)
где x1, ..., хт — неотрицательные переменные. В силу (27.3) и того, что р1 + р2 + ... + рт = 1, переменные x1, ..., хт удовлетворяют условию
 (27.5)
(27.5)
Но v есть не что иное, как наш гарантированный выигрыш; естественно, мы хотим сделать его максимальным, а значит, величину 1 / v минимальной.
Таким образом, задача решения игры свелась к математической задаче: найти неотрицательные значения переменных x1, ..., хт такие, чтобы они удовлетворяли линейным ограничениям-неравенствам (27.4) и обращали в минимум линейную функцию этих переменных:
 (27.6)
(27.6)
«Ба! — скажет читатель,— что-то знакомое!» И точно — перед нами не что иное, как задача линейного программирования. Таким образом, задача решения игры т×п свелась к задаче линейного программирования с п ограничениями-неравенствами и т переменными. Зная x1, ..., хт, можно по формулам (27.3) найти р1, р2, …, рт и, значит, оптимальную стратегию S*A и цену игры v.
Оптимальная стратегия игрока В находится совершенно аналогично, с той разницей, что В стремится хинизировать, а не максимизировать выигрыш, а значит, обратить не в минимум, а в максимум величину 1 / v, а в ограничениях-неравенствах вместо знаков ≥ будут стоять ≤. Пара задач линейного программирования, по которой находятся оптимальные стратегии(S*A,S*B), называется парой двойственных задач линейного программирования (доказано, что максимум линейной функции в одной из них равен минимуму линейной функции в другой, так что все в порядке—разных значений цены игры мы не получим).
Таким образом, решение игры т×п эквивалентно решению задачи линейного программирования. Нужно заметить, что и наоборот,— для любой задачи линейного программирования может быть построена эквивалентная ей задача теории игр (на том, как это делается, мы останавливаться не будем). Эта связь задач теории игр с задачами линейного программирования оказывается полезной не только для теорий игр, но и для линейного программирования. Дело в том, что существуют приближенные численные методы решения игр, которые в некоторых случаях (при большой размерности задачи) оказываются проще, чем «классические» методы линейного программирования.
Опишем один из самых простых численных методов решения игр — так называемый метод итераций (иначе — метод Брауна — Робинсон). Идея его в следующем. Разыгрывается «мысленный эксперимент», в котором стороны А и В поочередно применяют друг против друга свои стратегии, стремясь выиграть побольше (проиграть поменьше). Эксперимент состоит из ряда «партий» игры. Начинается он с того, что один из игроков (скажем, А) выбирает произвольно одну из своих стратегий Аi Противник (В) отвечает ему той из своих стратегий которая хуже всего для Аi, т. е. обращает его выигрыш при стратегии Ai в минимум. Дальше снова очередь А — он отвечает В той своей стратегией Ак, которая дает максимальный выигрыш при стратегии Вj противника. Дальше — снова очередь противника. Он отвечает нам той своей стратегией, которая является наихудшей не для последней, примененной нами, стратегии Ак а для смешанной стратегии, в которой до сих пор примененные стратегии Аi, Ак встречаются с равными вероятностями. И так далее: на каждом шаге итерационного процесса каждый игрок отвечает на очередной ход другого той своей стратегией, которая является оптимальной для него относительно смешанной стратегии другого, в которую все примененные до сих пор стратегии входят пропорционально частотам их применения. Вместо того чтобы вычислять каждый раз средний выигрыш, можно пользоваться просто «накопленным» за предыдущие ходы выигрышем и выбирать ту свою стратегию, при которой этот накопленный выигрыш максимален (минимален). Доказано, что такой метод сходится: при увеличении числа «партий» средний выигрыш на одну партию будет стремиться к цене игры, а частоты применения стратегий — к их вероятностям, в оптимальных
смешанных стратегиях игроков.
Впрочем, лучше всего можно понять итерационный метод на конкретном примере. Продемонстрируем его на примере игры 3×3 предыдущего параграфа (таблица 26.5). Чтобы не иметь дела с отрицательными числами, прибавим к элементам матрицы таблицы 26.5 число 5 (см. таблицу 27.6); при этом цена игры увеличится на 5, а решение S*A, S*b не изменится.
Начнем с произвольно выбранной стратегии игрока А,— например, со стратегии А3. В таблице 27.7 приведены первые 15 шагов итерационного процесса по методу Брауна — Робинсон (читатель может самостоятельно
продолжить расчеты). В первом столбце дан номер пар-
тии (пары выборов) А, во втором — номер i выбранной
в. данной партии стратегии игрока А. В последующих
трех столбцах — «накопленный выигрыш» за первые к
партий при тех стратегиях, Таблица 27.6
 которые применяли
которые применяли
игроки в предыдущих партиях и при стратегиях В1
В2, В3 игрока В в данной
партии (получается прибавлением элементов соответствующей строки к тому, что было строкой выше). Из этих накопленных выигрышей в таблице 27.7 подчеркнут минимальный (если их несколько, подчеркиваются все). Подчеркнутое число определяет ответный выбор игрока В в данной партии — он выбирает ту стратегию, которая соответствует подчеркнутому числу (если их несколько, берется любая). Таким образом определяется номер / оптимальной (в данной партии) стратегии В (ставится в следующем столбце). В последующих
Таблица 27.7
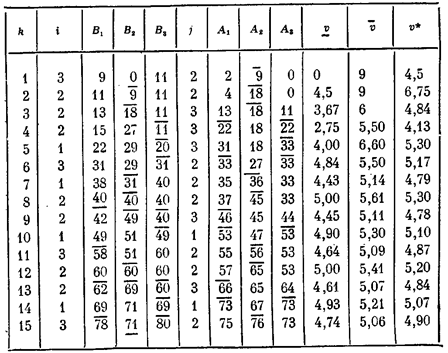
трех столбцах дается накопленный выигрыш за к партий соответственно при стратегиях А1,А2,Аз игрока А (получается прибавлением элементов столбцаBj к тому, что было строкой выше). Из этих значений в таблице 27.7 «надчеркнуто» максимальное; оно определяет выбор стратегии игрока А в следующей партии (строкой ниже). В последних трех столбцах таблицы 27.7 даны: v — нижняя оценка цены игры, равная минимальному накопленному выигрышу, деленному на число партий k; v — верхняя оценка цены игры, равная максимальному накопленному выигрышу, деленному на k;  — среднее арифметическое между ними (оно служит лучшей, чем нижняя и верхняя, приближенной оценкой цены игры).
— среднее арифметическое между ними (оно служит лучшей, чем нижняя и верхняя, приближенной оценкой цены игры).
Как видно, величина v* незначительно колеблется около цены игры v = 5 (цена исходной игры была 0, но мы прибавили к элементам матрицы по 5). Подсчитаем по таблице 27.7 частоты р1, р2, р3, q1, q2, q3 стратегий игроков. Получим:

что не так уж сильно отличается от вероятностей р1, р2, р3 q1, q2, q3 равных, как мы указывали раньше, для первой, второй и третьей стратегий соответственно 1/4 = 0,25, 1/2 = 0,50, 1/4 = 0,25. Такие сравнительно хорошие приближения мы получили уже при 15 итерациях — это обнадеживает! К сожалению, дальше процесс приближений будет идти не так резво. Сходимость метода Брауна — Робинсон, как показывает опыт, очень медленная, Существуют способы, позволяющий как бы «подхлестнуть» еле плетущийся процесс, но мы на них останавливаться не будем.
Очень важным преимуществом итерационного метода решения игр является то, что его трудоемкость сравнительно медленно возрастает с увеличением размерности игры т × n, тогда как трудоемкость метода линейного программирования растет при увеличении размерности задачи гораздо быстрее.
* * *
Таким образом, читатель получил некоторое представление о теории антагонистических игр и о методах решения матричных игр.
Скажем несколько критических слов по поводу этой теории и ее практической значимости. В свое время, когда теория игр еще только появилась, на нее возлагались большие надежды в смысле выбора решений для конфликтных ситуаций. Эти надежды оправдались лишь в малой степени.
Прежде всего, на практике не так уж часто встречаются строго антагонистические конфликты разве только в настоящих «играх» (шашки, шахматы, карты и т. п.). Вне этих искусственных ситуаций, где одна сторона стремится во что бы то ни стало обратить выигрыш в максимум, а другая — в минимум, такие конфликты почти не встречаются. Казалось бы, где, как не в области боевых действий должна была бы с успехом применяться теория игр? Ведь здесь мы встречаемся с самыми «свирепыми» антагонизмами, с самой резкой противоположностью интересов! Но оказывается, что конфликтные ситуации в этой области сравнительно редко удается свести к парным играм с нулевой суммой. Схема строгого антагонизма применима, как правило, только к операциям малого масштаба, ограниченным по значению. Например, сторона А — группа самолетов, налетающих на объект, сторона В— средства противовоздушной обороны объекта; первая стремится максимизировать вероятность уничтожения объекта, вторая — ее минимизировать. Здесь схема парной игры с нулевой суммой может найти применение. Но возьмем чуть более сложный пример: две группировки боевых единиц (типа танков, самолетов, кораблей) ведут бой. Каждая сторона стремится поразить как можно больше боевых единиц противника. В этом примере антагонизм ситуации теряет свою чистоту: она уже не сводится к парной игре с нулевой суммой. Если цели участников конфликта не прямо противоположны, а просто не совпадают, математическая модель становится много сложнее: мы уже не можем интересоваться выигрышем только одной стороны; возникает так называемая «биматричная игра», где каждый из участников стремится максимизировать свой выигрыш, а не просто минимизировать выигрыш противника. Теория таких ягр гораздо сложнее, чем теория антагонистических игр, а главное, из этой теории не удается получить четких рекомендаций по оптимальному образу действий сторон [26].
Второе критическое замечание будет касаться понятия «смешанных стратегий». Если речь идет о многократно повторяемой ситуации, в которой каждая сторона может легко (без дополнительных затрат) варьировать свое поведение от случая к случаю, оптимальные смешанные стратегии в самом деле могут повысить средний выигрыш. Но бывают ситуации, когда решение надо принять одно-единственное (например, выбрать план строительства системы оборонительных сооружений). Разумно ли будет «передоверить свой выбор случаю»,— грубо говоря, бросить монету, и если выпал герб, выбрать первый вариант плана, а если решка — второй? Вряд ли найдется такой руководитель, который в сложной и ответственной ситуации решится делать выбор случайным образом, хотя бы это и вытекало из принципов теории игр!
Наконец, последнее соображение: в теории игр считается, что каждому игроку известны все возможные стратегии противника, неизвестно лишь то, какой именно из них он воспользуется в данной партии игры. В реальном конфликте это обычно не так: перечень возможных стратегий противника как раз неизвестен, и наилучшим решением в конфликтной ситуации нередко будет именно выйти за пределы известных противнику стратегий, «ошарашить» его чем-то совершенно новым, непредвиденным!
Как видно из вышеизложенного, теория игр в качестве основы для выбора решения (даже в остроконфликтной ситуации) имеет много слабых мест. Значит ли это, что ее не нужно изучать, что она вовсе не нужна в исследовании операций? Нет, не значит. Теория игр ценна прежде всего самой постановкой задач, которая учит, выбирая решение в конфликтной ситуации, не забывать о том, что противник тоже мыслит, и учитывать его возможные хитрости и уловкп. Пусть рекомендации, вытекающие из игрового подхода, не всегда определенны и не всегда осуществимы — все же полезно, выбирая решение, ориентироваться, в числе других, и на игровую модель. Не надо только выводы, вытекающие из этой модели, считать окончательными и непререкаемыми[5]).
§ 28. Задачи теории статистических решений
Близкой по идеям и методам к теории игр является теория статистических решений. От теории игр она отличается тем, что неопределенная ситуация не имеет конфликтной окраски — никто никому не противодействует, но элемент неопределенности налицо. В задачах теории статистических решений неизвестные условия операции зависят не от сознательно действующего «противника» (или других участников конфликта), а от объективной действительности, которую в теории статистических решений принято называть «природой». Соответствующие ситуации часто называются «играми с природой». «Природа» мыслится как некая незаинтересованная инстанция («равнодушная природа»,—по Пушкину), «поведение» которой неизвестно, но во всяком случае не злонамеренно.
Казалось бы, отсутствие сознательного противодействия упрощает задачу выбора решения. Оказывается, нет: не упрощает, а усложняет. Правда, принимающему решение в «игре с природой» в самом деле «легче» добиться успеха (ведь ему никто не мешает!), но ему «труднее» обосновать свой выбор. В игре против сознательного противника элемент неопределенности отчасти снимается тем, что мы «думаем» за противника, «принимаем» за него решение, самое неблагоприятное для нас самих. В игре же с природой такая концепция не подходит: кто ее знает, как она, матушка, себя поведет? Поэтому теория статистических решений —наиболее «шаткая» в смысле рекомендаций наука. Все же у нее есть право на существование и на внимание со стороны лиц, занимающихся исследованием операций.
Рассмотрим игру с природой: у нас (сторона А) имеется т возможных стратегий А1, А2, ..., Ат, что касается обстановки, то о ней можно сделать п предположений: П1, П2, ..., Пn. Рассмотрим их как «стратегии природы». Наш выигрыш aij при каждой паре стратегий Аi, Пi задан матрицей (таблица 28.1).
Требуется выбрать такую стратегию игрока А (чистую или, может быть, смешанную, если это возможно), которая является более выгодной по сравнению с другими.
С первого взгляда кажется, что эта задача похожа на игру двух игроков А и П с противоположными интересами и должна решаться теми же методами. Но это не совсем так. Отсутствие противодействия со стороны природы делает ситуацию качественно другой[6]).
Если даже в матрице игры с природой нет одной доминирующей над всеми другими, все же полезно посмотреть, нет ли в ней дублирующих стратегий и уступающих другим при всех условиях (как мы это делали, упрощая матрицу игры). Но здесь есть одна тонкость: так мы можем уменьшить только число стратегий игрока Л, но не игрока Я —ему ведь все равно, много или мало мы выиграем! Предположим, что «чистка» матрицы произведена, и ни дублирующих, ни заведомо невыгодных игроку А стратегий в ней нет.
Чем же все-таки руководствоваться при выборе решения? Вполне естественно, должна учитываться матрица выигрышей (аij). Однако в каком-то смысле картина ситуации, которую дает матрица (аij), неполна и не отражает должным образом достоинств и недостатков каждого решения.
Поясним эту (далеко не простую) мысль. Предположим, что выигрыш аij при нашей стратегии Ai и состоянии природы Пj больше, чем при нашей стратегии Ak и состоянии природы Пi: аij > аkl. Но за счет чего больше? За счет того, что мы удачно выбрали стратегию Ai? Необязательно. Может быть, просто состояние природы Пj выгоднее нам, чем Пi. Например, состояние природы «нормальные условия» для любой операции выгоднее, чем «наводнение», «землетрясение» и т. п. Желательно ввести такие показатели, которые не просто давали бы выигрыш при данной стратегии в каждой ситуации, но отражали бы «удачность» или «неудачность» выбора данной стратегии в данной ситуации.
С этой целью в теории решений вводится понятие «риска». Риском rij игрока Л при пользовании стратегией Ai в условиях Пj называется разность между выигрышем, который мы получили бы, если бы знали условия Пj и выигрышем, который мы получим, не зная их и выбирая стратегию Ai.
Очевидно, если бы мы (игрок A) знали состояние природы Пj, мы выбрали бы ту стратегию, при которой наш выигрыш максимален. Этот выигрыш, максимальный в столбце Пj мы уже раньше встречали и обозначили βj. Чтобы получить риск rij, нужно из βj вычесть фактический выигрыш аij:
 (28.1)
(28.1)
Для примера возьмем матрицу выигрышей (аij)(таблица 28.3) и построим для нее матрицу рисков (rij) (таблица 28.4).
При взгляде на матрицу рисков (таблица 28.4) нам становятся яснее некоторые черты данной «игры с природой». Так, в матрице выигрышей (аij)(таблица 28.3)

во второй строке первый и последний элементы были равны друг другу: а12 = a34 = 3. Однако эти выигрыши совсем не равноценны в смысле удачного выбора стратегии: при состоянии природы П1 мы могли выиграть самое большее 4, и наш выбор стратегии А2 почти совершенно хорош; а вот при состоянии П4 мы могли бы, выбрав стратегию А и получить на целых 6 единиц больше, т. е. выбор стратегии А2 очень плох. Риск — это «плата за отсутствие информации»: в таблице 28.4 r21 = 1, r24 = 6 (тогда как выигрыши аij в том и другом случае одинаковы). Естественно, нам хотелось бы минимизировать риск, сопровождающий выбор решения.
Итак, перед нами — две постановки задачи о выборе решения: при одной нам желательно получить максимальный выигрыш, при другой — минимальный риск.
Мы знаем, что самый простой случай неопределенности — это «доброкачественная» или стохастическая неопределенность, когда состояния природы имеют какие-то вероятности Q1, Q2, ..., Qn и эти вероятности нам известны. Тогда естественно (со всеми оговорками, сделанными по этому поводу в § 5) выбрать ту стратегию, для которой среднее значение выигрыша, взятое по строке, максимально:

(28.2)
Любопытно отметить, что та же стратегия, которая обращает в максимум средний выигрыш, обращает в минимум и средний риск:

(28.3)
так что в случае стохастической неопределенности оба подхода («от выигрыша» и «от риска») дают одно и то же оптимальное решение.
Давайте чуточку «испортим» нашу неопределенность и допустим, что вероятности Q1, Q2,…, Qn в принципе существуют, но нам неизвестны. Иногда в этом случае предполагают все состояния природы равновероятными (так называемый «принцип недостаточного основания» Лапласа), но вообще-то это делать не рекомендуется. Все-таки обычно более или менее ясно, какие состояния более, а какие — менее вероятны. Для того чтобы найти ориентировочные значения вероятностей Q1, Q2,…, Qn можно, например, воспользоваться методом экспертных оценок (см. § 5). Хоть какие-то ориентировочные значения вероятностей состояний природы все же лучше, чем полная неизвестность. Неточные значения вероятностей состояний природы в дальнейшем могут быть «скорректированы» с помощью специально поставленного эксперимента. Эксперимент может быть как «идеальным», полностью выясняющим состояние природы, так и неидеальным, где вероятности состояний уточняются по косвенным данным. Каждый эксперимент, разумеется, требует каких-то затрат, и возникает вопрос: окупаются ли эти затраты возрастанием эффективности? Оказывается, «идеальный» эксперимент имеет смысл проводить только в случае, когда его стоимость меньше, чем минимальный средний риск (см., например, [61).
Однако не будем больше заниматься случаем стохастической неопределенности, а возьмем случай «дурной неопределенности», когда вероятности состояний природы либо вообще не существуют, либо не поддаются оценке даже приближенно. Ну что же? Обстановка неблагоприятна для принятия «хорошего» решения — попытаемся найти хотя бы не самое худшее.
Здесь все зависит от точки зрения на ситуацию, от позиции исследователя, от того, какими бедами грозит неудачный выбор решения. Опишем несколько возможных подходов, точек зрения (или, как говорят, несколько «критериев» для выбора решения).
1. Максиминный критерий Вальда. Согласно этому критерию игра с природой ведется как игра с разумным, причем агрессивным противником, делающим все для того, чтобы помешать нам достигнуть успеха. Оптимальной считается стратегия, при которой гарантируется выигрыш в любом случае не меньший, чем «нижняя цена игры с природой»;
(28.4)
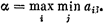 (28.4)
(28.4)
Если руководствоваться этим критерием, олицетворяющим «позицию крайнего пессимизма», надо всегда ориентироваться на худшие условия, зная наверняка, что «хуже этого не будет». Очевидно, такой подход — «перестраховочный», естественный для того, кто очень боится проиграть,— не является единственно возможным, но как крайний случай он заслуживает рассмотрения.
2. Критерий минимаксного риска Сэвиджа. Этот критерий — тоже крайне пессимистический, но при выборе оптимальной стратегии советует ориентироваться не на выигрыш, а на риск. Выбирается в качестве оптимальной та стратегия, при которой 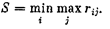 величина риска в наихудших условиях минимальна:
величина риска в наихудших условиях минимальна:
(28.5)
Сущность такого подхода в том, чтобы всячески избегать большого риска при принятии решения. В смысле «пессимизма» критерий Сэвиджа сходен с критерием Вальда, но самый «пессимизм» здесь понимается по-другому.
3. Критерий пессимизма-оптимизма Гурвица. Этот критерий рекомендует при выборе решения не руко- водствов^аться ни крайним пессимизмом («всегда рассчитывай на худшее!»), ни крайним, легкомысленным оптимизмом («авось кривая вывезет!»). Согласно этому критерию выбирается стратегия из условия

(28.6)
где х — «коэффициент пессимизма», выбираемый между нулем и единицей. При х = 1 критерий Гурвица превращается в критерий Вальда; при х = 0 — в критерий «крайнего оптимизма», рекомендующий выбрать ту стратегию, при которой самый большой выигрыш в строке максимален. При 0 < х < 1 получается нечто среднее между тем и другим. Коэффициент х выбирается из субъективных соображений — чем опаснее ситуация, чем больше мы хотим в ней «подстраховаться», чем менее наша склонность к риску, тем ближе к единице выбирается х.
При желании можно построить критерий, аналогичный H, исходя не из выигрыша, а из риска, но мы на этом не будем останавливаться.
«Что же,— спросит читатель,— выбор критерия — субъективен, выбор коэффициента х — тоже субъективен, значит и решение тоже принимается субъективно, т. е., грубо говоря, произвольно? Где же тут наука? При чем тут математика? Может быть, лучше было бы просто, без математических затей, выбрать решение по своему произволу?»
В какой-то мере читатель прав — выбор решения в условиях неопределенности всегда условен, субъективен. И все же в какой-то (ограниченной) мере математические методы полезны и тут. Прежде всего, они позволяют привести игру с природой к матричной форме, что далёко не всегда бывает просто, особенно когда стратегий много (в наших примерах их было очень мало). Кроме того, они позволяют заменить простое лицезрение матрицы выигрышей (или рисков), от которого, когда матрица велика, может просто «зарябить в глазах», последовательным численным анализом ситуации с разных точек зрения, выслушать рекомендации каждой из них и, наконец, остановиться на чем-то определенном. Это аналогично обсуждению вопроса с различных позиций, а в споре, как известно, рождается истина. Так что не ждите от теории решений окончательных, непререкаемых рекомендаций — единственное, чем она может помочь — это советом...
Если рекомендации, вытекающие из различных критериев, совпадают — тем лучше, значит, можно смело выбрать рекомендуемое решение: оно скорее всего «не подведет». Если же, как это часто бывает, рекомендации противоречат друг другу, не надо забывать, что у нас голову на плечах. Задумаемся над этими рекомендациями, выясним, насколько к разным ре-
зультатам они приводят, уточним свою точку зрения
и произведем окончательный выбор. Не надо забывать,
что в любых задачах обоснования решений некоторый
| Таблица 28.5 |
 произвол неизбежен — хо-
произвол неизбежен — хо-
тя бы при построении ма-
тематической модели, вы-:
боре показателя эффективности. Вся математика, применяемая в исследовании операций, не отменяет этого произвола, а позволяет только «поставить его на свое место».
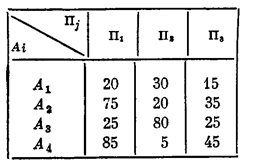
Рассмотрим элементарный пример «игры с природой» 4 X 3, матрица выигрышей которой (aij) дана в таблице 28.5. Поглядим на матрицу и попробуем сразу, без расчетов, указать, какой стратегией пользоваться? Несмотря на малый
размер матрицы, это не так-то легко.
Теперь попробуем помочь себе, пользуясь критериями Вальда, Сэвиджа и Гурвица, причем в последнем возьмем х = 0,6 (перевес чуть-чуть в сторону пессимизма). Что-то они нам скажут?
1. Слово имеет критерий Вальда. Подсчитаем минимумы по строкам (см. таблицу 28.6) и выберем ту стратегию, при которой минимум строки максимален (равен 25). Это — стратегия A3.
Т а б л и ц а 28.6

2. Слово имеет критерий Сэвиджа. Перейдем от матрицы выигрышей (таблица 28.6) к матрице рисков (таблица 28.7), в правом дополнительном столбце запишем максимальное в строке значение риска Y*.
Из чисел правого столбца минимальное (60) соответствуетстратегиям А2 и А3 значит, обе они оптимальны по Сэвиджу.
| Таблица 28.7 |
Т а б л и ц а 28.7 
3.  Слово имеет критерий Гурвица (при x = 0,6). Опять перепишем таблицу 28.5, но на этот раз в правых трех дополнительных столбцах поставим: минимум строки ai, ее максимум w1 и величину hi = хаi + (1 — х) wi, округленную до целых единиц (см. таблицу 28.8).
Слово имеет критерий Гурвица (при x = 0,6). Опять перепишем таблицу 28.5, но на этот раз в правых трех дополнительных столбцах поставим: минимум строки ai, ее максимум w1 и величину hi = хаi + (1 — х) wi, округленную до целых единиц (см. таблицу 28.8).
Максимальное значение hi = 47 соответствует стратегии А3.
Итак, в данном случае все три критерия согласно говорят в пользу стратегии А3, которую есть все основания выбрать.
| Таблица 28.8 |
А теперь возьмем случай, когда между критериями возникает «спор». Матрица выигрышей (аij) (с заранее выписанными столбцами минимумов строк аi, максимумами строк wi и значениями hi (при x= 0,6) дана в таблице 28.9.
По критерию Вальда оптимальной является стратегия А1, по критерию Гурвица с х = 0,6 — стратегия
| Таблица 28.9 |
 A3. Посмотрим, что скажет критерий Сэвиджа. Матрица рисков с дополнительным столбцом, содержащим максимумы строк дана в таблице 28.10.
A3. Посмотрим, что скажет критерий Сэвиджа. Матрица рисков с дополнительным столбцом, содержащим максимумы строк дана в таблице 28.10.
Минимальным в последнем столбце является число 38, так что критерий Сэвиджа, так же как- и критерий Гурвица, «голосует» за стратегию А3.
Над этим стоит поразмыслить. Если мы очень боимся малого выигрыша «11», который нас может постигнуть при стратегии А3, ну что же — выберем стратегию А1, рекомендуемую крайне осторожным критерием Вальда, при котором мы, по крайней мере, можем себе гарантировать выигрыш «19», а может быть, и больше. Если же наш пессимизм не так уж мрачен, пожалуй, надо остановиться на стратегии А3, рекомендуемой двумя из трех критериев.
| Таблица 28.10 |

Читатель, конечно заметил, что тут мы говорим на каком-то нематематическом языке, а скорее на языке «рассуждений и здравого смысла». Что поделаешь — в неопределенности ничего хорошего нет, и при отсутствии нужной информации никакая математика не поможет нам в однозначном выборе «оптимального» решения. Жизнь есть жизнь, будущее полно неопределенностей, и нам зачастую приходится принимать отнюдь не строго оптимальные, а «приемлемые» решения, при обсуждении которых разные «подходы» и «критерии» выступают в качестве как бы спорящих сторон.
В заключение отметим следующее: все три критерия (Вальда, Сэвиджа и Гурвица) были сформулированы нами для чистых стратегий, но каждый из них может быть распространен и на смешанные, подобно тому, как мы это делали в теории игр. Однако смешанные стратегии в игре с природой имеют лишь' ограниченное (главным образом, теоретическое) значение. Если в игре против сознательного противника смешанные статегии иногда имеют смысл как «трюк», вводящий в заблуждение противника, то в игре против «равнодушной природы» этот резон отпадает. Кроме того, смешанные стратегии приобретают смысл только при многократном повторении игры. А если уж мы ее повторяем, то неизбежно начинают вырисовываться какие-то вероятностные черты ситуации, и мы ими можем воспользоваться для того, чтобы применить «стохастический подход» к задаче, а он, как мы знаем, смешанных стратегий не дает. Кроме того, в ситуациях с «дурной» неопределенностью, когда нам мучительно не хватает информации, главная задача — эту информацию получить, а не выдумывать хитроумные методы, позволяющие без нее обойтись. Одна из основных задач теории статистических решений — это как раз планировании эксперимента, цель которого — выяснение или уточнение каких-то данных. На вопросах планирования эксперимента мы здесь останавливаться не будем: это отдельный предмет, требующий серьезного внимания. По этому вопросу мы отошлем читателя к специальным руководствам [29, 30], а также к интересно написанной популярной книге [27]. Основной принцип теории планирования эксперимента состоит в том, что любое принятое заранее решение должно пересматриваться с учетом полеченной новой информации.
| * * * |
Таким образом, наш краткий обзор, посвященный задачам, принципам и методологии исследования операций, закончен. В нем автор стремился ознакомить читателя не только с возможностями, но и с ограничениями математических методов, применяемых для обоснования решений. Главное — ни один из этих методов не избавляет человека от необходимости думать. Но не просто думать, а пользоваться при этом математическими расчетами. Помня, что, по меткому выражению Хемминга,— «главная цель расчетов — не цифры, а понимание».
ЛИТЕРАТУРА
1. С а а т и Т. JI. Математические методы исследования операций.— М.: Воениздат, 1963 (около 25 п. л.).
2. В е н т ц е л ь Е. С. Теория вероятностей (первые Шаги).—М.: Знание, 1977 (около 3,5 п. л.).
3. П о д и н о в с к и й В. В., Гаврилов В. М. Оптими- зация по последовательно применяемым критериям.— М.: Советское радио, 1975 (около 8 п. л.).
4 Карпелевич Ф. И., Садовский JI. Е. Элементы линейной алгебры и линейного программирования.— М.: Наука,
1967 (около 15 п. л.).
5. Ю д и н Д. Б., Гольштейн Е. Г. Линейное программирование.— М.: Наука, 1967 (около 40 п. л.).
6. В е н т ц е л ь Е. С. Исследование операций.— М.: Советское радио, 1972 (около 35 п. л.).
7. В а г н е р Г. Основы исследования операций.— М.: Мир, 1972 (в трех томах, общий объем около 80 п. л.).
8. 3 у х о в и ц к и й С. И., Авдеева Л. И. Линейное и выпуклое программирование.— М.: Наука, 1964 (около 17 п. л.).
9. Турин Л. С., Д ы м а р с к и й Я. С., Меркулов А. Д. Задачи и методы оптимального распределения ресурсов.— М.: Советское радио, 1968 (около 25 п. л.).
10. Б е л л м а н Р. Динамическое программирование.— М.: Иностранная литература, 1960 (около 25 п. л.),
И. Вентце ль Е. С. Элементы динамического программирования.— М.: Наука, 1964 (около 10 п. л.).
12. В е н т ц е л ь Е. С. Теория вероятностей.— М.: Наука, 1964 (около 35 п. л.).
13. Р о з е н б е р г В. Я., Прохоров А. И. Что такое теория массового обслуживания.— М.: Советское радио, 1S62 (около 13 п. л.).
14. О в ч а р о в Л. А. Прикладные задачи теории массового обслуживания.—М.: Машиностроение, 1969 (около 18 п. л.).
15. К о ф м а н А., К р ю о н Р. Массовое обслуживание, теория и применения.—М.: Прогресс, 1965 (около 20 п. л.).
16. Г н е д е н к о Б. В., Коваленко И. Н. Введение в теорию массового обслуживания.— М.: Наука, 1966 (около 22 п. л.).
17. С а а т и Т. JL Элементы теории массового обслуживания и ее приложения.— М.: Советское радио, 1971 (около 32 п. л.).
18. Платонов Г. А., Ф а й н б е р г М. А., Штиль- м а н М. С. Поезда, пассажиры и... математика.— М.: Транспорт, 1977 (около 10 п. л.).
19. Севастьянов Б. А. Формулы Эрланга в телефонии.— Труды III математического съезда, т. IV, изд. АН СССР, 1959.
20. Г м у р м а н В. Е. Теория вероятностей и математическая статистика.— М.: Высшая школа, 1977 (около 22 п. л.).
21. Вентце ль Е. С. Исследование операций,—М.: Знание, 1976 (около 3,5 п. л.).
22. С о б о л ь И. М. Метод Монте-Карло.— М.: Физматгиз,
1968 (около 3,5 п. л.).
23. Исследование операций (методологические аспекты).—* М.: Наука, 1972 (около 4 п. л.).
24. В е н т ц е л ь Е. С. Элементы теории игр.— М.: Физматгиз, 1969 (около 4 п. л.).
25. М а к - К и н с и Дж. Введение в теорию игр.— М.: Физматгиз, 1960 (около 20 п. л.).
26. JI ь ю с Р. Д., Райфа X. Игры и решения.— М.: Иностранная литература, 1961 (около 40 п. л.).
27. Хургин Я. И. Да, нет или может быть...—М.: Наука, 1977 (около 10 п, л.).
28. Гер ме й е р Ю. Б. Введение в теорию исследования операций.— М.: Наука, 1971 (около 20 п. л.).
29. Налимов В. В. Теория эксперимента.—М.: Наука, 1971 (около 10 п. л.).
30. В а л ъ д А. Последовательный анализ.— М.: Физматгиз, 1960 (около 17 п. л.).
31. Ю д и н Д. Б. Математические методы управления в условиях неполной информации.— М.: Советское радио, 1974 (около 30 п. л.)«
[1] Нечто похожее иногда случается, когда люди, мало знакомые с теорией вероятностей, моделируют методом Монте-Карло задачи, имеющие аналитическое решение.
[2] Точнее, обладают одинаковой плотностью вероятности,
[3] Этот довод подозрительно напоминает рассуждения г-жи Простаковой («Недоросль» Фонвизина) по поводу ненужности изучения географии: «Да извозчики-то на что? Это их дело. Это и наука-то не дворянская. Дворянин только скажи; повези меня туда, свезут, куда изволишь»,
[4] Термин «седловая точка» взят из геометрии — так называется точка на поверхности, где одновременно достигается минимум по одной координате и максимум по другой
[5] Изложенная здесь точка зрення автора на роль и значение теории игр вовсе не общепринята. Некоторые авторы, напротив, считают игровые подходы в исследовании операций основными (см., например, [28]).
[6] К сожалению, нередки случаи, когда люди, малоискушенные в исследовании операций, встретившись на практике с такой ситуацией, забывают о «равнодушии» природы и сразу же начинают решать задачу методами теории антагонистичен ских игр. Такие рекомендации встречаются и в книгах (прей имущественно популярных).
А. Ясауи атындағы Халықаралық қазақ-түрік университеті
| <== предыдущая лекция | | | следующая лекция ==> |
| Нейрон як об’єкт Психофізіології. Структурно функціональні особливості нейрону. | | | Розрахункова схема колони |