
Головна сторінка Випадкова сторінка
КАТЕГОРІЇ:
АвтомобіліБіологіяБудівництвоВідпочинок і туризмГеографіяДім і садЕкологіяЕкономікаЕлектронікаІноземні мовиІнформатикаІншеІсторіяКультураЛітератураМатематикаМедицинаМеталлургіяМеханікаОсвітаОхорона праціПедагогікаПолітикаПравоПсихологіяРелігіяСоціологіяСпортФізикаФілософіяФінансиХімія
Слово як одиниця лексичної системи.
Дата добавления: 2015-09-19; просмотров: 838
|
|
Механическими колебаниями называют движения тел, повторяющиеся точно (или приблизительно) через одинаковые промежутки времени. Закон движения тела, совершающего колебания, задается с помощью некоторой периодической функции времени x = f(t). Примерами простых колебательных систем могут служить груз на пружине или математический маятник
Механические колебания, как и колебательные процессы любой другой физической природы, могут быть свободными и вынужденными. Простейшим видом колебательного процесса являются простые гармонические колебания, которые описываются уравнением x = xm cos (ωt + φ0).
Здесь x – смещение тела от положения равновесия, xm – амплитуда колебаний, т. е. максимальное смещение от положения равновесия, ω – циклическая или круговая частота колебаний, t – время. Величина, стоящая под знаком косинуса φ = ωt + φ0 называется фазой гармонического процесса. При t = 0 φ = φ0, поэтому φ0 называют начальной фазой. Минимальный интервал времени, через который происходит повторение движения тела, называется периодом колебаний T. Физическая величина, обратная периоду колебаний, называется частотой колебаний: 
Частота колебаний f показывает, сколько колебаний совершается за 1 с. Единица частоты – герц (Гц). Частота колебаний f связана с циклической частотой ω и периодом колебаний T соотношениями: 
../../../../../../Program Files/Physicon/Open Physics 2.5 part 1/design/images/Fwd_h.gif../../../../../../Program Files/Physicon/Open Physics 2.5 part 1/design/images/Bwd_h.gifСвободные колебания.
Свободные колебания совершаются под действием внутренних сил системы после того, как система была выведена из положения равновесия.
Уравнение x = xm cos (ωt + φ0). называется уравнением свободных колебаний. Следует обратить внимание на то, что физические свойства колебательной системы определяют только собственную частоту колебаний ω0 или период T. Такие параметры процесса колебаний, как амплитуда xm и начальная фаза φ0, определяются способом, с помощью которого система была выведена из состояния равновесия в начальный момент времени.
Превращения энергии при свободных механических колебаниях
При свободных механических колебаниях кинетическая и потенциальная энергии периодически изменяются. При максимальном отклонении тела от положения равновесия его скорость, а следовательно, и кинетическая энергия обращаются в нуль. В этом положении потенциальная энергия колеблющегося тела достигает максимального значения. Для груза на пружине потенциальная энергия – это энергия упругих деформаций пружины. Для математического маятника – это энергия в поле тяготения Земли.
Когда тело при своем движении проходит через положение равновесия, его скорость максимальна. Тело проскакивает положение равновесия по закону инерции. В этот момент оно обладает максимальной кинетической и минимальной потенциальной энергией. Увеличение кинетической энергии происходит за счет уменьшения потенциальной энергии. При дальнейшем движении начинает увеличиваться потенциальная энергия за счет убыли кинетической энергии и т. д.
Таким образом, при гармонических колебаниях происходит периодическое превращение кинетической энергии в потенциальную и наоборот.
Если в колебательной системе отсутствует трение, то полная механическая энергия при свободных колебаниях остается неизменной.
Для груза на пружине 
Для малых колебаний математического маятника 
Здесь hm – максимальная высота подъема маятника в поле тяготения Земли, xm и υm = ω0xm – максимальные значения отклонения маятника от положения равновесия и его скорости.
Превращения энергии при свободных механических колебаниях в отсутствие трения можно проиллюстрировать графически. Сумма  остается неизменной.
остается неизменной.

| 
|
| Рисунок 2.4.1. Превращения энергии при свободных колебаниях. | Рисунок 2.4.2. Затухающие колебания. |
В реальных условиях любая колебательная система находится под воздействием сил трения (сопротивления). При этом часть механической энергии превращается во внутреннюю энергию теплового движения атомов и молекул, и колебания становятся затухающими (рис. 2.4.2).
../../../../../../Program Files/Physicon/Open Physics 2.5 part 1/design/images/Fwd_h.gif../../../../../../Program Files/Physicon/Open Physics 2.5 part 1/design/images/Bwd_h.gifВынужденные колебания. Резонанс.
Колебания, совершающиеся под воздействием внешней периодической силы, называются вынужденными.
Внешняя сила совершает положительную работу и обеспечивает приток энергии к колебательной системе. Она не дает колебаниям затухать, несмотря на действие сил трения.
Если частота ω внешней силы приближается к собственной частоте ω0, возникает резкое возрастание амплитуды вынужденных колебаний. Это явление называется резонансом. Явление резонанса может явиться причиной разрушения мостов, зданий и других сооружений, если собственные частоты их колебаний совпадут с частотой периодически действующей силы, возникшей, например, из-за вращения несбалансированного мотора.
Механические волны
Если в каком-нибудь месте твердой, жидкой или газообразной среды возбуждены колебания частиц, то вследствие взаимодействия атомов и молекул среды колебания начинают передаваться от одной точки к другой с конечной скоростью. Процесс распространения колебаний в среде называется волной.
Механические волны бывают разных видов. Если при распространении волны частицы среды испытывают смещение в направлении, перпендикулярном направлению распространения, такая волна называется поперечной. Примером волны такого рода могут служить волны, бегущие по натянутому резиновому жгуту (рис. 2.6.1) или по струне.
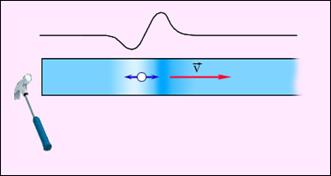
Если смещение частиц среды происходит в направлении распространения волны, такая волна называется продольной. Волны в упругом стержне (рис. 2.6.2) или звуковые волны в газе являются примерами таких волн.

| 
|
| Рисунок 2.6.1. Распространение поперечного волнового импульса по натянутому резиновому жгуту. | Рисунок 2.6.2. Распространение продольного волнового импульса по упругому стержню. |
Волны на поверхности жидкости имеют как поперечную, так и продольную компоненты.
Как в поперечных, так и в продольных волнах не происходит переноса вещества в направлении распространения волны. В процессе распространения частицы среды лишь совершают колебания около положений равновесия. Однако волны переносят энергию колебаний от одной точки среды к другой.
Характерной особенностью механических волн является то, что они распространяются в материальных средах (твердых, жидких или газообразных). Существуют волны, которые способны распространяться и в пустоте (например, световые волны). Для механических волн обязательно нужна среда, обладающая способностью запасать кинетическую и потенциальную энергию. Следовательно, среда должна обладать инертными и упругими свойствами.
Продольные механические волны могут распространяться в любых средах – твердых, жидких и газообразных.
, поперечные волны не могут существовать в жидкой или газообразной средах.
Длиной волны λ называют расстояние между двумя соседними точками на оси OX, колеблющимися в одинаковых фазах. Расстояние, равное длине волны λ, волна пробегает за период Т, следовательно, λ = υT, где υ – скорость распространения волны.
Звук
Звуковыми волнами или просто звуком принято называть волны, воспринимаемые человеческим ухом. Диапазон звуковых частот лежит в пределах приблизительно от 20 Гц до 20 кГц. Волны с частотой менее 20 Гц называются инфразвуком, а с частотой более 20 кГц – ультразвуком. Волны звукового диапазона могут распространяться не только в газе, но и в жидкости (продольные волны) и в твердом теле (продольные и поперечные волны). Однако волны в газообразной среде – среде нашего обитания – представляют особый интерес. Изучением звуковых явлений занимается раздел физики, который называют акустикой.
При распространении звука в газе атомы и молекулы колеблются вдоль направления распространения волны. Это приводит к изменениям локальной плотности ρ и давления p. Звуковые волны в газе часто называют волнами плотности или волнами давления.
Скорость звука сильно зависит от свойств газа. Чем легче газ, тем больше скорость звука в этом газе. Так, например, в воздухе (M = 29·10–3 кг/моль) при нормальных условиях υ = 331,5 м/с, в гелии (M = 4·10–3 кг/моль) υ = 970 м/с, в водороде (M = 2·10–3 кг/моль) υ = 1270 м/с.
В жидкостях и твердых телах скорость звуковых волн еще больше. В воде, например, υ = 1480 м/с (при 20 °С), в стали υ = 5–6 км/с.
При восприятии различных звуков человеческое ухо оценивает их прежде всего по уровню громкости, зависящей от потока энергии или интенсивности звуковой волны. Воздействие звуковой волны на барабанную перепонку зависит от звукового давления, т. е. амплитуды p0 колебаний давления в волне. Человеческое ухо является совершенным созданием Природы, способным воспринимать звуки в огромном диапазоне интенсивностей: от слабого писка комара до грохота вулкана. Порог слышимости соответствует значению p0 порядка 10–10 атм, т. е. 10–5 Па. При таком слабом звуке молекулы воздуха колеблются в звуковой волне с амплитудой всего лишь 10–7 см! Болевой порог соответствует значению p0 порядка 10–4 атм или 10 Па. Таким образом, человеческое ухо способно воспринимать волны, в которых звуковое давление изменяется в миллион раз. Так как интенсивность звука пропорциональна квадрату звукового давления, то диапазон интенсивностей оказывается порядка 1012! Такой огромный диапазон человеческого уха эквивалентен использованию одного и того же прибора для измерения диаметра атома и размеров футбольного поля.
Для сравнения укажем, что при обычных разговорах людей в комнате интенсивность звука приблизительно в 106 раз превышает порог слышимости, а интенсивность звука при рок-концерте приближается к болевому порогу.
Еще одной характеристикой звуковых волн, определяющей их слуховое восприятие, является высота звука. Колебания в гармонической звуковой волне воспринимаются человеческим ухом как музыкальный тон. Колебания высокой частоты воспринимаются как звуки высокого тона, колебания низкой частоты – как звуки низкого тона. Звуки, издаваемые музыкальными инструментами, а также звуки человеческого голоса могут сильно различаться по высоте тона и по диапазону частот. Так, например, диапазон наиболее низкого мужского голоса – баса – простирается приблизительно от 80 до 400 Гц, а диапазон высокого женского голоса – сопрано – от 250 до 1050 Гц.
| <== предыдущая лекция | | | следующая лекция ==> |
| Практична робота № 5 | | | ПРАКТИЧНИЙ БЛОК |