
Головна сторінка Випадкова сторінка
КАТЕГОРІЇ:
АвтомобіліБіологіяБудівництвоВідпочинок і туризмГеографіяДім і садЕкологіяЕкономікаЕлектронікаІноземні мовиІнформатикаІншеІсторіяКультураЛітератураМатематикаМедицинаМеталлургіяМеханікаОсвітаОхорона праціПедагогікаПолітикаПравоПсихологіяРелігіяСоціологіяСпортФізикаФілософіяФінансиХімія
ЛЬВІВ 2012
Дата добавления: 2015-09-19; просмотров: 534
|
|
Text 1. Strong AI and Searle's Chinese Room

| Internet Assignment: |
1. Use the Internet search engine and find additional information about the supporters and opponents of strong AI. Start your search with such key-words as: Chinese room, Turing test, Searle's program, Schank's algorithm, Holstadter's argument.
2. "Can a computer have a mind?" Provide answers to this question, discussing it with Internet community. Consult Roger Penrose's Penguin book "The Emperor's New Mind", if necessary.
There is a point of view, referred to as strong AI which adopts a rather extreme position on these issues. According to strong AI, not only would the devices just referred to indeed be intelligent and have minds, etc., but mental qualities of a sort can be attributed to the logical functioning of any computational device, even the very simplest mechanical ones, such as a thermostat. The idea is that mental activity is simply the carrying out of some well-defined sequence of operations, frequently referred to as an algorithm. I shall be more precise later on, as to what an algorithm actually is. For the moment, it will be adequate to define an algorithm simply as a calculational procedure of some kind. In the case of a thermostat, the algorithm is extremely simple: the device registers whether the temperature is greater or smaller than the setting, and then it arranges that the circuit be disconnected in the former case and connected in the latter. For any significant kind of mental activity of a human brain, the algorithm would have to be something vastly more complicated but, according to the strong-AI view, an algorithm nevertheless. It would differ very greatly in degree from the simple algorithm of the thermostat, but need not differ in principle. Thus, according to strong AI, the difference between the essential functioning of a human brain (including all its conscious manifestations) and that of a thermostat lies only in this much greater complication (or perhaps 'higher-order structure' or 'self-referential properties', or some other attribute that one might assign to an algorithm) in the case of a brain. Most importantly, all mental qualities – thinking, feeling, intelligence, understanding, consciousness – are to be regarded, according to this view, merely as aspects of this complicated functioning; that is to say, they are features merely of the algorithm being carried out by the brain.
The virtue of any specific algorithm would lie in its performance, namely in the accuracy of its results, its scope, its economy, and the speed with which it can be operated. An algorithm purporting to match what is presumed to be operating in a human brain would need to be a stupendous thing. But if an algorithm of this kind exists for the brain and the supporters of strong AI would certainly claim that it does – then it could in principle be run on a computer. Indeed it could be run on any modern general purpose electronic computer, were it not for limitations of storage space and speed of operation. (The justification of this remark will come later, when we come to consider the universal Turing machine.) It is anticipated that any such limitations would be overcome for the large fast computers of the not-too-distant future. In that eventuality, such an algorithm, if it could be found, would presumably pass the Turing test. The supporters of strong AI would claim that whenever the algorithm were run it would, in itself: experience feelings; have a consciousness; be a mind.
By no means everyone would be in agreement that mental states and algorithms can be identified with one another in this kind of way. In particular, the American philosopher John Searle (1980, 1987) has strongly disputed that view. He has cited examples where simplified versions of the Turing test have actually already been passed by an appropriately programmed computer, but he gives strong arguments to support the view that the relevant mental attribute of 'understanding' is, nevertheless, entirely absent. One such example is based on a computer program designed by Roger Schank (Schank and Abelson 1977). The aim of the program is to provide a simulation of the understanding of simple stories like: 'A man went into a restaurant and ordered a hamburger. When the hamburger arrived it was burned to a crisp, and the man stormed out of the restaurant angrily, without paying the bill or leaving a tip.' For a second example: 'A man went into a restaurant and ordered a hamburger; when the hamburger came he was very pleased with it; and as he left the restaurant he gave the waitress a large tip before paying his bill.' As a test of 'understanding' of the stories, the computer is asked whether the man ate the hamburger in each case (a fact which had not been explicitly mentioned in either story). To this kind of simple story and simple question the computer can give answers which are essentially indistinguishable from the answers an English-speaking human being would give, namely, for these particular examples, 'no' in the first case and 'yes' in the second. So in this very limited sense a machine has already passed a Turing test!
The question that we must consider is whether this kind of success actually indicates any genuine understanding on the part of the computer – or, perhaps, on the part of the program itself. Searle's argument that it does not is to invoke his concept of a “Chinese room”. He envisages first of all, that the stories are to be told in Chinese rather than English surely an inessential change – and that all the operations of the computer's algorithm for this particular exercise are supplied (in English) as a set of instructions for manipulating counters with Chinese symbols on them. Searle imagines himself doing all the manipulations inside a locked room. The sequences of symbols representing the stories, and then the questions, are fed into the room through some small slot. No other information whatever is allowed in from the outside. Finally, when all the manipulations are complete, the resulting sequence is fed out again through the slot. Since all these manipulations are simply carrying out the algorithm of Schank's program, it must turn out that this final resulting sequence is simply the Chinese for ‘yes’ or ‘no’, as the case may be, giving the correct answer to the original question in Chinese about a story in Chinese. Now Searle makes it quite clear that he doesn't understand a word of Chinese, so he would not have the faintest idea what the stories are about. Nevertheless, by correctly carrying out the series of operations which constitute Schank's algorithm (the instructions for this algorithm having been given to him in English) he would be able to do as well as a Chinese person who would indeed understand the stories. Searle's point – and I think it is quite a powerful one – is that the mere carrying out of a successful algorithm does not in itself imply that any understanding has taken place. The (imagined) Searle, locked in his Chinese room, would not understand a single word of any of the stories!
A number of objections have been raised against Searle's argument. I shall mention only those that 1 regard as being of serious significance. In the first place, there is perhaps something rather misleading in the phrase 'not understand a single word', as used above. Understanding has as much to do with patterns as with individual words. While carrying out algorithms of this kind, one might well begin to perceive something of the patterns that the symbols make without understanding the actual meanings of many of the individual symbols. For example, the Chinese character for 'hamburger' (if. indeed, there is such a thing) could be replaced by that for some other dish, say 'chow mein', and the stories would not be significantly affected. Nevertheless, it seems to me to be reasonable to suppose that in fact very little of the stories' actual meanings (even regarding such replacements as being unimportant) would come through if one merely kept following through the details of such an algorithm.
In the second place, one must take into account the fact that the execution of even a rather simple computer program would normally be something extraordinarily lengthy and tedious if carried out by human beings manipulating symbols. (This is, after all, why we have computers to do such things for us!) If Searle were actually to perform Schank's algorithm in the way suggested, he would be likely to be involved with many days, months, or years of extremely boring work in order to answer just a single question – not an altogether plausible activity for a philosopher! However, this does not seem to me to be a serious objection since we are here concerned with matters of principle and not with practicalities. The difficulty arises more with a putative computer program which is supposed to have sufficient complication to match a human brain and thus to pass the Turing test proper. Any such program would have to be horrendously complicated. One can imagine that the operation of this program, in order to effect the reply to even some rather simple Turing-test question, might involve so many steps that there would be no possibility of any single human being carrying out the algorithm by hand within a normal human lifetime. Whether this would indeed be the case is hard to say, in the absence of such a program. But, in any case, this question of extreme complication cannot, in my opinion, simply be ignored. It is true that we are concerned with matters of principle here, but it is not inconceivable to me that there might be some 'critical' amount of complication in an algorithm which it is necessary to achieve in order that the algorithm exhibit mental qualities. Perhaps this critical value is so large that no algorithm, complicated to that degree, could conceivably be carried out by hand by any human being, in the manner envisaged by Searle.
Searle himself has countered this last objection by allowing a whole team of human non-Chinese- speaking symbol manipulators to replace the previous single inhabitant (‘himself’) of his Chinese room. To get the numbers large enough, he even imagines replacing his room by the whole of India, its entire population (excluding those who understand Chinese!) being now engaged in symbol manipulation. Though this would be in practice absurd, it is not in principle absurd, and the argument is essentially the same as before: the symbol manipulators do not understand the story, despite the strong-AI claim that the mere carrying out of the appropriate algorithm would elicit the mental quality of “understanding”. However, now another objection begins to loom large. Are not these individual Indians more like the individual neurons in a person's brain than like the whole brain itself? No-one would suggest that neurons, whose firings apparently constitute the physical activity of a brain in the act of thinking, would themselves individually understand what that person is thinking, so why expect the individual Indians to understand the Chinese stories? Searle replies to this suggestion by pointing out the apparent absurdity of India, the actual country, understanding a story that none of its individual inhabitants understands. A country, he argues, like a thermostat or an automobile, is not in the 'business of understanding', whereas an individual person is.
This argument has a good deal less force to it than the earlier one. I think that Searle's argument is at its strongest when there is just a single person carrying out the algorithm, where we restrict attention to the case of an algorithm which is sufficiently uncomplicated for a person actually to carry it out in less than a lifetime. I do not regard his argument as rigorously establishing that there is not some kind of disembodied 'understanding' associated with the person's carrying out of that algorithm, and whose presence does not impinge in any way upon his own consciousness. However, I would agree with Searle that this possibility has been rendered rather implausible, to say the least. I think that Searle's argument has a considerable force to it, even if it is not altogether conclusive. It is rather convincing in demonstrating that algorithms with the kind of complication that Schank's computer program possesses cannot have any genuine understanding whatsoever of the tasks that they perform; also, it suggests (but no more) that no algorithm, no matter how complicated, can ever, of itself alone, embody genuine understanding – in contradistinction to the claims of strong AI.
There are, as far as I can see, other very serious difficulties with the strong-AI point of view. According to strong AI, it is simply the algorithm that counts. It makes no difference whether that algorithm is being effected by a brain, an electronic computer, an entire country of Indians, a mechanical device of wheels and cogs, or a system of water pipes. The viewpoint is that it is simply the logical structure of the algorithm that is significant for the 'mental state' it is supposed to represent, the particular physical embodiment of that algorithm being entirely irrelevant. As Searle points out, this actually entails a form of 'dualism'. Dualism is a philosophical viewpoint espoused by the highly influential seventeenth century philosopher and mathematician Rene Descartes, and it asserts that there are two separate kinds of substance: 'mind-stuff and ordinary matter. Whether, or how, one of these kinds of substance might or might not be able to affect the other is an additional question. The point is that the mind-stuff is not supposed to be composed of matter, and is able to exist independently of it. The mind-stuff of strong AI is the logical structure of an algorithm. As I have just remarked, the particular physical embodiment of an algorithm is something totally irrelevant. The algorithm has some kind of disembodied 'existence' which is quite apart from any realization of that algorithm in physical terms. How seriously we must take this kind of existence is a question I shall need to return to in the next chapter. It is part of the general question of the Platonic reality of abstract mathematical objects. For the moment I shall sidestep this general issue and merely remark that the supporters of strong AI do indeed seem to be taking the reality at least of algorithms seriously, since they believe that algorithms form the 'substance' of their thoughts, their feelings, their understanding, their conscious perceptions. There is a remarkable irony in this fact that, as Searle has pointed out, the standpoint of strong AI seems to drive one into an extreme form of dualism, the very viewpoint with which the supporters of strong AI would least wish to be associated!
This dilemma lies behind the scenes of an argument put forward by Douglas Hofstadter (1981) – himself a major proponent of the strong-AI view – in a dialogue entitled 'A Conversation with Einstein's Brain'. Hofstadter envisages a book, of absurdly monstrous proportions, which is supposed to contain a complete description of the brain of Albert Einstein. Any question that one might care to put to Einstein can be answered, just as the living Einstein would have, simply by leafing through the book and carefully following all the detailed instructions it provides. Of course 'simply' is an utter misnomer, as Hofstadter is careful to point out. But his claim is that in principle the book is completely equivalent, in the operational sense of a Turing test, to a ridiculously slowed-down version of the actual Einstein. Thus, according to the contentions of strong AI, the book would think, feel understand, be aware, just as though it were Einstein himself, but perhaps living at a monstrously slowed-down rate (so that lo the book-Einstein the world outside would seem to flash by at a ridiculously speeded-up rate). Indeed, since the book is supposed to be merely a particular embodiment of the algorithm which constitutes Einstein's 'self, it would actually be Einstein.
But now a new difficulty presents itself. The book might never be opened, or it might be continually pored over by innumerable students and searchers after truth. How would the book 'know' the difference? Perhaps the book would not need to be opened, its information being retrieved by means of  -ray tomography, or some other technological wizardry. Would Einstein's awareness be enacted only when the book is being so examined? Would he be aware twice over if two people chose to ask the book the same question at two completely different times? Or would that entail two separate and temporally distinct instances of the same state of Einstein's awareness? Perhaps his awareness would be enacted only if the book is changed? After all, normally when we are aware of something we receive information from the outside world which affects our memories, and the states of our minds are indeed slightly changed. If so, does this mean that it is (suitable) changes in algorithms (and here I am including the memory store as part of the algorithm) which are to be associated with mental events rather than (or perhaps in addition to) the activation of algorithms? Or would the book-Einstein remain completely self-aware even if it were never examined or disturbed by anyone or anything? Hofstadter touches on some of these questions, but he does not really attempt to answer or to come to terms with most of them.
-ray tomography, or some other technological wizardry. Would Einstein's awareness be enacted only when the book is being so examined? Would he be aware twice over if two people chose to ask the book the same question at two completely different times? Or would that entail two separate and temporally distinct instances of the same state of Einstein's awareness? Perhaps his awareness would be enacted only if the book is changed? After all, normally when we are aware of something we receive information from the outside world which affects our memories, and the states of our minds are indeed slightly changed. If so, does this mean that it is (suitable) changes in algorithms (and here I am including the memory store as part of the algorithm) which are to be associated with mental events rather than (or perhaps in addition to) the activation of algorithms? Or would the book-Einstein remain completely self-aware even if it were never examined or disturbed by anyone or anything? Hofstadter touches on some of these questions, but he does not really attempt to answer or to come to terms with most of them.
What does it mean to activate an algorithm, or to embody it in physical form? Would changing an algorithm be different in any sense from merely discarding one algorithm and replacing it with another? What on earth does any of this have to do with our feelings of conscious awareness? The reader (unless himself or herself a supporter of strong AI) may be wondering why I have devoted so much space to such a patently absurd idea. In fact, I do not regard the idea as intrinsically an absurd one – mainly just wrong! There is, indeed some force in the reasoning behind strong AI which must be reckoned with, and this I shall try to explain. There is, also, in my opinion, a certain appeal in some of the ideas – if modified appropriately – as I shall also try to convey. Moreover, in my opinion, the particular contrary view expressed by Searle also contains some serious puzzles and seeming absurdities, even though, to a partial extent, I agree with him!
Searle, in his discussion, seems to be implicitly accepting that electronic computers of the present-day type, but with considerably enhanced speed of action and size of rapid-access store (and possibly parallel action) may well be able to pass the Turing test proper, in the not-too-distant future. He is prepared to accept the contention of strong AI (and of most other 'scientific' viewpoints) that 'we are the instantiations of any number of computer programs'. Moreover, he succumbs to: 'Of course the brain is a digital computer. Since everything is a digital computer, brains are too. Searle maintains that the distinction between the function of human brains (which can have minds) and of electronic computers (which, he has argued, cannot) both of which might be executing the same algorithm, lies solely in the material construction of each. He claims, but for reasons he is not able to explain, that the biological objects (brains) can have 'intentionality' and 'semantics', which he regards as defining characteristics of mental activity, whereas the electronic ones cannot. In itself this does not seem to me to point the way towards any helpful scientific theory of mind. What is so special about biological systems, apart perhaps from the 'historical' way in which they have evolved (and the fact that we happen to be such systems), which sets them apart as the objects allowed to achieve intentionality or semantics? The claim looks to me suspiciously like a dogmatic assertion, perhaps no less dogmatic, even, than those assertions of strong AI which maintain that the mere enacting of an algorithm can conjure up a state of conscious awareness!
In my opinion Searle, and a great many other people, have been led astray by the computer people. And they, in turn, have been led astray by the physicists. (It is not the physicists' fault. Even they don't know everything!) The belief seems to be widespread that, indeed, 'everything is a digital computer'. It is my intention, in this book, to try to show why, and perhaps how, this need not be the case.
Text 2. The Insolubility of Hilbert's Problem

| Internet Assignment: |
Use the Internet and provide answers to these questions:
1. What directions and tendencies in the 19th century maths gave implications and led D.Hilbert to formulating those particular problems?
2. How do the 20th century mathematicians estimate the solution of any problem in D.Hilbert’s list?
3. Who solved D.Hilbert’s 10th problem? When?
4. What is the contribution of the Ukrainian mathematicians to the solution of the problems under study?
5. Are the unsolved problems the very essence of maths?
We now come to the purpose for which Turing originally put forward his ideas, the resolution of Hilbert's broad-ranging Entscheidungsproblem: is there some mechanical procedure for answering all mathematical problems, belonging to some broad, but well-defined class? Turing found that he could phrase his version of the question in terms of the problem of deciding whether or not the 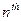 Turing machine would actually ever stop when acting on the number
Turing machine would actually ever stop when acting on the number  . This problem was referred to as the halting problem. It is an easy matter to construct an instruction list for which the machine will not stop for any number m (for example,
. This problem was referred to as the halting problem. It is an easy matter to construct an instruction list for which the machine will not stop for any number m (for example, 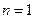 or
or 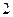 , as given above, or any other case where there are no stop instructions whatever). Also there are many instruction lists for which the machine would always stop, whatever number it is given (e.g.
, as given above, or any other case where there are no stop instructions whatever). Also there are many instruction lists for which the machine would always stop, whatever number it is given (e.g. 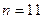 ); and some machines would stop for some numbers but not for others. One could fairly say that a putative algorithm is not much use when it runs forever without stopping. That is no algorithm at all. So an important question is to be able to decide whether or not Tn applied to m actually ever gives any answer! If it does not (i.e. if the calculation does not stop), then I shall write
); and some machines would stop for some numbers but not for others. One could fairly say that a putative algorithm is not much use when it runs forever without stopping. That is no algorithm at all. So an important question is to be able to decide whether or not Tn applied to m actually ever gives any answer! If it does not (i.e. if the calculation does not stop), then I shall write 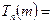 □.
□.
(Included in this notation would be those situations where the Turing machine runs into a problem at some stage because it finds no appropriate instruction to tell it what to do – as with the dud machines such as 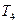 and
and 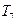 considered above. Also, unfortunately, our seemingly successful machine
considered above. Also, unfortunately, our seemingly successful machine 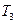 , must now also be considered a dud:
, must now also be considered a dud: 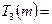 , because the result of the action of
, because the result of the action of 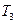 is always just blank tape, whereas we need at least one 1 in the output in order that the result of the calculation be assigned a number! The machine
is always just blank tape, whereas we need at least one 1 in the output in order that the result of the calculation be assigned a number! The machine 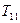 is, however, legitimate since it produces a single 1. This output is the tape numbered 0, so we have
is, however, legitimate since it produces a single 1. This output is the tape numbered 0, so we have 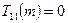 for all m.)
for all m.)
It would be an important issue in mathematics to be able to decide when Turing machines stop. For example, consider the equation:
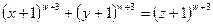 .
.
(If technical mathematical equations are things that worry you, don't be put off! This equation is being used only as an example, and there is no need to understand it in detail.) This particular equation relates to a famous unsolved problem in mathematics – perhaps the most famous of all. The problem is this: is there any set of natural numbers w, x, y, z for which this equation is satisfied? The famous statement known as 'Fermat's last theorem', made in the margin of Diophantus's Arithmetica, by the great seventeenth century French mathematician Pierre de Fermat (1601-1665), is the assertion that the equation is never satisfied.[12] Though a lawyer by profession (and a contemporary of Descartes), Fermat was the finest mathematician of his time. He claimed to have a truly wonderful proof of his assertion, which the margin was too small to contain; but to this day no-one has been able to reconstruct such a proof nor, on the other hand, to find any counter-example to Fermat's assertion!
It is clear that given the quadruple of numbers (w, x, y, z), it is a mere matter of computation to decide whether or not the equation holds. Thus we could imagine a computer algorithm which runs through all the quadruples of numbers one after the other, and stops only when the equation is satisfied. (We have seen that there are ways of coding finite sets of numbers, in a computable way, on a single tape, i.e. simply as single numbers, so we can 'run through' all the quadruples by just following the natural ordering of these single numbers.) If we could establish that this algorithm does not stop, then we would have a proof of the Fermat assertion.
In a similar way it is possible to phrase many other unsolved mathematical problems in terms of the Turing machine halting problem. Such an example is the 'Goldbach conjecture', which asserts that every even number greater than 2 is the sum of two prime numbers.[13] It is an algorithmic process to decide whether or not a given natural number is prime since one needs only to test its divisibility by numbers less than itself, a matter of only finite calculation. We could devise a Turing machine which runs through the even numbers 6, 8,10, 12, 14, ... trying all the different ways of splitting them into pairs of odd numbers
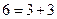 ,
, 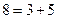 ,
, 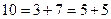 ,
,
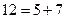 ,
, 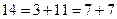 , …
, …
and testing to make sure that, for each such even number, it splits to some pair for which both members are prime. (Clearly we need not test pairs of even summands, except 2 + 2, since all primes except 2 are odd.) Our machine is to stop only when it reaches an even number for which none of the pairs into which that number splits consists of two primes. In that case we should have a counter-example to the Goldbach conjecture, namely an even number (greater than 2) which is not the sum of two primes. Thus if we could decide whether or not this Turing machine ever stops, we should have a way of deciding the truth of the Goldbach conjecture also.
A natural question arises: how are we to decide whether or not any particular Turing machine (when fed with some specific input) will ever stop? For many Turing machines this might not be hard to answer; but occasionally, as we have seen above, the answer could involve the solution of an outstanding mathematical problem. So, is there some algorithmic procedure for answering the general question – the halting problem – completely automatically? Turing showed that indeed there is not.
His argument was essentially the following. We first suppose that, on the contrary, there is such an algorithm.[14] Then there must be some Turing machine H which 'decides' whether or not the 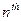 Turing machine, when acting on the number m, eventually stops. Let us say that it outputs the tape numbered 0 if it does not stop and 1 if it does:
Turing machine, when acting on the number m, eventually stops. Let us say that it outputs the tape numbered 0 if it does not stop and 1 if it does:
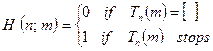 .
.
Here, one might take the coding of the pair 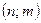 to follow the same rule as we adopted for the universal machine
to follow the same rule as we adopted for the universal machine 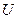 . However this could run into the technical problem that for some number
. However this could run into the technical problem that for some number 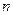 (e.g.
(e.g. 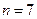 ), Tn is not correctly specified; and the marker 111110 would be inadequate to separate n from m on the tape. To obviate this problem, let us assume that n is coded using the expanded binary notation rather than just the binary notation, with m in ordinary binary, as before. Then the marker 110 will actually be sufficient to separate n from m. The use of the semicolon in
), Tn is not correctly specified; and the marker 111110 would be inadequate to separate n from m on the tape. To obviate this problem, let us assume that n is coded using the expanded binary notation rather than just the binary notation, with m in ordinary binary, as before. Then the marker 110 will actually be sufficient to separate n from m. The use of the semicolon in  , as distinct from the comma in
, as distinct from the comma in 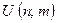 , is to indicate this change.
, is to indicate this change.
Now let us imagine an infinite array, which lists all the outputs of all possible Turing machines acting on all the possible different inputs. The 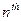 row of the array displays the output of the
row of the array displays the output of the 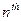 Turing machine, as applied to the various inputs 0,1, 2, 3,4, … :
Turing machine, as applied to the various inputs 0,1, 2, 3,4, … :
| m → | … | |||||||||
| n ↓ | ||||||||||
| □ | □ | □ | □ | □ | □ | □ | □ | □ | … | |
| … | ||||||||||
| … | ||||||||||
| … | ||||||||||
| … | ||||||||||
| □ | □ | □ | □ | … | ||||||
| □ | □ | □ | □ | … | ||||||
| … | ||||||||||
| □ | □ | □ | □ | □ | □ | … | ||||
| . | . | . | . | … | ||||||
| . | . | . | . | |||||||
| . | . | . | . | |||||||
| … | ||||||||||
| . | . | . | . | |||||||
| . | . | . | . | |||||||
| . | . | . | . |
In the above table I have cheated a little, and not listed the Turing machines as they are actually numbered. To have done so would have yielded a list that looks much too boring to begin with, since all the machines for which n is less than 11 yield nothing but Ds, and for 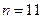 itself we get nothing but 0s. In order to make the list look initially more interesting, I have assumed that some much more efficient coding has been achieved. In fact I have simply made up the entries fairly randomly, just to give some kind of impression as to what its general appearance could be like.
itself we get nothing but 0s. In order to make the list look initially more interesting, I have assumed that some much more efficient coding has been achieved. In fact I have simply made up the entries fairly randomly, just to give some kind of impression as to what its general appearance could be like.
I am not asking that we have actually calculated this array, say by some algorithm. (In fact, there is no such algorithm, as we shall see in a moment.) We are just supposed to imagine that the true list has somehow been laid out before us, perhaps by God! It is the occurrence of the Ds which would cause the difficulties if we were to attempt to calculate the array, for we might not know for sure when to place a Din some position since those calculations simply run on forever!
However, we could provide a calculational procedure for generating the table if we were allowed to use our putative 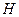 , for
, for 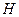 would tell us where the □s actually occur. But instead, let us use
would tell us where the □s actually occur. But instead, let us use 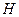 to eliminate every □ by replacing each occurrence with 0. This is achieved by preceding the action of
to eliminate every □ by replacing each occurrence with 0. This is achieved by preceding the action of 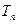 on
on  by the calculation
by the calculation  ; then we allow
; then we allow 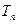 to act on m only if
to act on m only if 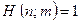 (i.e. only if the calculation
(i.e. only if the calculation 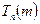 actually gives an answer), and simply write 0 if
actually gives an answer), and simply write 0 if 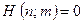 (i.e. if
(i.e. if 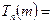 □ ). We can write our new procedure (i.e. that obtained by preceding
□ ). We can write our new procedure (i.e. that obtained by preceding 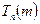 by the action of
by the action of 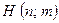 )as
)as
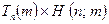 .
.
(Here I am using a common mathematical convention about the ordering of mathematical operations: the one on the right is to be performed first. Note that, symbolically, we have □ x 0 = 0.) The table for this now reads:
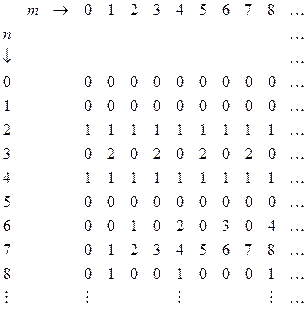
Note that, assuming H exists, the rows of this table consist of computable sequences. (By a computable sequence I mean an infinite sequence whose successive values can be generated by an algorithm; i.e. there is some Turing machine which, when applied to the natural numbers m = 0,1, 2, 3, 4, 5, … in turn, yields the successive members of the sequence.) Now, we take note of two facts about this table. In the first place, every computable sequence of natural numbers must appear somewhere (perhaps many times over) amongst its rows. This property was already true of the original table with its Ds. We have simply added some rows to replace the 'dud' Turing machines (i.e. the ones which produce at least one D). In the second place, the assumption having been made that the Turing machine H actually exists, the table has been computably generated (i.e. generated by some definite algorithm), namely by the procedure 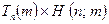 . That is to say, there is some Turing machine
. That is to say, there is some Turing machine 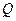 which, when acting on the pair of numbers
which, when acting on the pair of numbers 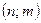 produces the appropriate entry in the table. For this, we may code
produces the appropriate entry in the table. For this, we may code 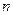 and
and  on
on 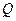 's tape in the same way as for
's tape in the same way as for 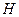 , and we have
, and we have
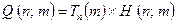 .
.
We now apply a variant of an ingenious and powerful device, the 'diagonal slash' of Georg Cantor. Consider the elements of the main diagonal, marked now with bold figures:
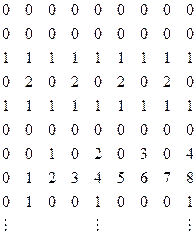
These elements provide some sequence 0, 0, 1, 2, 1,0, 3, 7, 1, … to each of whose terms we now add 1:
1, 1, 2, 3, 2, 1, 4, 8, 2, … .
This is clearly a computable procedure and, given that our table was computably generated, it provides us with some new computable sequence, in fact with the sequence 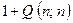 , i.e.
, i.e.

(since the diagonal is given by making m equal to n). But our table contains every computable sequence, so our new sequence must be somewhere in the list. Yet this cannot be so! For our new sequence differs from the first row in the first entry, from the second row in the second entry, from the third row in the third entry, and so on. This is manifestly a contradiction. It is the contradiction which establishes what we have been trying to prove, namely that the Turing machine H does not in fact exist! There is no universal algorithm for deciding whether or not a Turing machine is going to stop.
Another way of phrasing this argument is to note that, on the assumption that H exists, there is some Turing machine number, say k, for the algorithm (diagonal process!) 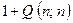 , so we have
, so we have
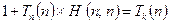 .
.
But if we substitute 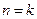 in this relation we get
in this relation we get
 .
.
This is a contradiction because if 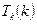 stops we get the impossible relation
stops we get the impossible relation
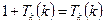
(since 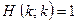 ), whereas if
), whereas if 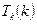 does not stop (so
does not stop (so 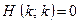 ) we have the equally inconsistent
) we have the equally inconsistent
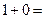 □.
□.
The question of whether or not a particular Turing machine stops is a perfectly well-defined piece of mathematics (and we have already seen that, conversely, various significant mathematical questions can be phrased as the stopping of Turing machines). Thus, by showing that no algorithm exists for deciding the question of the stopping of Turing machines, Turing showed (as had Church, using his own rather different type of approach) that there can be no general algorithm for deciding mathematical questions. Hilbert's Entscheidungsproblem has no solution!
This is not to say that in any individual case we may not be able to decide the truth, or otherwise, of some particular mathematical question; or decide whether or not some given Turing machine will stop. By the exercise of ingenuity, or even of just common sense, we may be able to decide such a question in a given case. (For example, if a Turing machine's instruction list contains no stop order, or contains only stop orders, then common sense alone is sufficient to tell us whether or not it will stop!) But there is no one algorithm that works for all mathematical questions, nor for all Turing machines and all numbers on which they might act.
It might seem that we have now established that there are at least some undecidable mathematical questions. However, we have done nothing of the kind! We have not shown that there is some especially awkward Turing machine table for which, in some absolute sense, it is impossible to decide whether or not the machine stops when it is fed with some especially awkward number – indeed, quite the reverse, as we shall see in a moment. We have said nothing whatever about the insolubility of single problems, but only about the algorithmic insolubility of families of problems. In any single case the answer is either 'yes' or 'no', so there certainly is an algorithm for deciding that particular case, namely the algorithm that simply says 'yes', when presented with the problem, or the one that simply says 'no', as the case may be! The difficulty is, of course, that we may not know which of these algorithms to use. That is a question of deciding the mathematical truth of a single statement, not the systematic decision problem for a family of statements. It is important to realize that algorithms do not, in themselves, decide mathematical truth. The validity of an algorithm must always be established by external means.
| <== предыдущая лекция | | | следующая лекция ==> |
| МІНІСТЕРСТВО ОСВІТИ І НАУКИ УКРАЇНИ | | | Індивідуальна робота №2 |