Коректор: А.О. Ковальова

Дата добавления: 2015-09-19; просмотров: 604

Прецессия – отклонение главной оси гироскопа в сторону, перпендикулярную направлению воздействия возмущающей силы.

Для определения направления скорости и направления прецессионного движения рассмотрим рис. 4, а.

Положительным направлением вектора является то, откуда вращение ротора гироскопа будет видно против часовой стрелки. Вектор направлен в точку, которую называют полюсом гироскопа.

Рис. 4. Параметры движения трехстепенного гироскопа:

а) Направление скорости и прецессии; б) Гироскопические моменты и моменты сил инерции

Приложим к вектору возмущающую силу 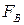. Момент этой силы будет направлен в ту сторону (в полюс силы), откуда под ее действием поворот оси гироскопа был бы виден против часовой стрелки. Под действием момента произойдет изменение момента количества движения гироскопа:

. (2.1.2)

Из элементарного векторного треугольника имеем:

, (2.1.3)

где – бесконечно малая величина угла прецессии.

Скорость изменения угла прецессии есть производная от :

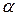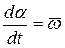. (2.1.4)

Подставив в уравнение (2) уравнения (3) и (4), получим:

. (2.1.5)

Из теоретической механики известно, что в векторном произведении все векторы взаимно перпендикулярны. Направление вектора 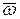будет перпендикулярно к плоскости, в которой лежат векторы и :

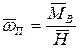. (2.1.6)

Направления прецессии определяется правилом: под действием приложенной силы полюс гироскопа идет по кратчайшему расстоянию к полюсу силы.

Гироскопическая реакция– возникновение у свободного гироскопа под действием искусственно создаваемого прецессионного движения момента , равного по величине и обратного по направлению тому возмущающему моменту, который бы вызвал это прецессионное движение:

. (2.1.7)

Рассмотрим уравнения движения гироскопа, пользуясь рис. 4, б.

Полные дифференциальные уравнения движения гироскопа содержат нелинейные члены, и их решение может быть найдено только на основе использования приближенных методов. Однако, как показывает анализ, с высокой степенью точности решение этих уравнений может быть найдено, если отбросить нелинейные члены. Это объясняется тем, что в современных технических гироскопах:

перемещение гироскопа по оси Z в вертикальной плоскости по углу достаточно невелико;

угловые скорости и также сравнительно малы.

Отсюда примем, что .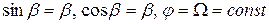

Тогда система дифференциальных уравнений движения гироскопа может быть записана в следующем виде:

, (2.1.8)

где ; ;

А, В – экваториальные моменты инерции ротора относительно осей Х и У соответственно;

А_1, В₁ – моменты инерции внутреннего кольца подвеса относительно осей Х и У;

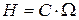– кинетический момент инерции ротора;

С – осевой момент инерции ротора;

– моменты внешних сил, действующие на гироскоп относительно соответствующих осей.

Выражение (2.1.8) представляет собой систему технических уравнений движения гироскопа около неподвижной точки.

В системе (2.1.8) составляющие моменты 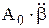и представляют собой моменты сил инерции, а и – гироскопические моменты.

Технические уравнения удобны для практического использования и обеспечивают достаточную точность.

Следует иметь в виду, что приведенные технические уравнения составлены для случая, когда угол достаточно мал. При больших значениях угла технические уравнения запишутся в следующем виде:

(2.1.9)

При расчетах пренебрегают инерционными членами 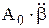, и пользуются укороченными техническими уравнениями:

(2.1.10)

Эти уравнения обеспечивают необходимую точность расчетов при определении ошибок современных артиллерийских гироскопических приборов.