День рівноапостольних Кирила та Мефодія. День слов’янської писемності та культури

Дата добавления: 2015-10-01; просмотров: 587

Гамма-функция, Г-функция, Г-функция Эйлера, эйлеров интеграл 2-го рода, — одна из важнейших трансцендентных функций математического анализа, распространяющая понятие факториала на случай комплексных значений z. Г.-ф. впервые введена Леонардом Эйлером (1729); она определяется формулой

Если действительная часть числа z положительна, то можно также пользоваться формулой

(Эйлеров интеграл 2-го рода).

Если n натуральное число, то Γ(n) = (n − 1)! Интеграл

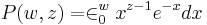
наз. неполной гамма-функцией. Основные соотношения для Г.-ф.:

Γ(z + 1) = zΓ(z) (функциональное уравнение);

(формула дополнения), отсюда

где при (формула Стирлинга).

В действительной области Γ(x) > 0 для x > 0 и принимает знак ( − 1)^{k + 1} на участках

Для всех действительных x справедливо неравенство

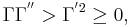
т. е. все ветви как | Γ(x) | , так и ln | Γ(x) | — выпуклые функции. Свойство логарифмической выпуклости определяет Г.-ф. среди всех решений функционального уравнения Γ(1 + x) = xΓ(x) с точностью до постоянного множителя. Для положительных x Г.-ф. имеет единственный минимум при , равный

Локальные минимумы функции | Γ(x) | при образуют последовательность, стремящуюся к нулю. Г.-ф. представляет собой мероморфную функцию с простыми полюсами в точках Функция 1 / Γ(z) является целой функцией 1-го порядка максимального типа:

где C — постоянная Эйлера. Эта формула послужила отправным пунктом для создания теории разложения целых функций в бесконечные произведения. При этом асимптотически где

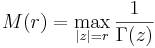
Через Г.-ф. выражается большое число определённых интегралов, бесконечных произведений и сумм рядов. Она играет важную роль в теории специальных функций — цилиндрических, гипергеометрических и др. Г.-ф. и её свойства используются также в аналитической теории чисел.

ПРАКТИЧЕСКАЯ ЧАСТЬ

Для вычисления гамма-функции используется аппроксимация её логарифма. Для аппроксимации гамма-функции на интервале x>0 используется следующая формула (для комплексных z):

Г(z+1)=(z+g+0.5)z+0.5exp((z+g+0.5)) 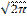[a0+a1/(z+1)+a2/(z+2)+...+an/(z+n)+eps]

Эта формула похожа на аппроксимацию Стирлинга, но в ней имеется корректирующая серия. Для значений g=5 и n=6, проверено, что величина погрешности не превышает 2*10^-10. Более того, погрешность не превышает этой величины на всей правой половине комплексной плоскости: z > 0.

Для получения (действительной) гамма-функции на интервале x>0 используется рекуррентная формула Г(z+1)=zГ(z) и вышеприведенная аппроксимация Г(z+1). Кроме того, можно заметить, что удобнее аппроксимировать логарифм гамма-функции, чем ее саму. Во-первых, при этом потребуется вызов только одной математической функции - логарифма, а не двух - экспоненты и степени (последняя все равно использует вызов логарифма), во-вторых, гамма-функция - быстро растущая для больших x, и аппроксимация ее логарифмом снимает вопросы переполнения.

Для аппроксимации Ln(Г(х) - логарифма гамма-функции - получается формула:

log(Г(x))=(x+0.5)log(x+5.5)-(x+5.5)+ log(C0(C1+C2/(x+1)+C3/(x+2)+...+C7/(x+8))/x)

Значения коэффициентов Ck - табличные данные.

Сама гамма-функция получается из ее логарифма взятием экспоненты.